沉没辊湿模态分析与试验研究
2020-08-17王兴东涂琪瑞李友荣鲁光涛
王兴东 ,涂琪瑞 ,李友荣 ,鲁光涛
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉 430081;2.武汉科技大学机械国家级实验教学示范中心,湖北 武汉 430081)
1 引言
冷轧带钢热镀锌线的沉没辊浸没于锌液中,影响其动态特性的因素较复杂[1-2],且具有沉没辊类似结构特征的物体,浸没在流体介质中其动态特性与真空中相比,存在显著差异[3-4]。沉没辊作为热镀锌线的重要部件,其振动特性直接影响带钢的镀锌涂层质量。而在分析其振动特性的过程中必须考虑锌液流场的耦合作用,即对结构进行湿模态分析。
关于湿模态许多学者对此做了丰富的研究,文献[5]对涡轮机进行了自由悬挂状态下空气中与水中的模态试验,试验结果表明,同一振型中涡轮机在空气中与水中的固有频率差异依赖于水的附加质量效应。文献[6-7]分别对油底壳和输油管进行流固耦合的模态分析,并与试验对比验证了该计算方法的准确性。文献[8]通过结构-声学耦合模型计算水下悬臂梁的频率变化,并与模态试验对比,研究了悬臂梁厚度在水下振动频率的变化关系。文献[9]通过模态试验研究薄膜在不同密度空气中的固有频率的变化,结果表明气体的密度越大,其自振频率的变化越明显。文献[10]对带有任意边缘裂纹的自由圆板进行流固耦合动力特性研究,研究表明:水体引起固有频率降低,且随着模态阶数的增加而减小。上述研究中,以沉没辊为研究对象,且通过试验研究沉没辊湿模态变化的较少。
针对上述问题,对沉没辊采用有限元仿真方法对其在水中的固有频率进行了研究,计算了自由与约束状态下前7 阶固有频率,并对沉没辊分别进行了自由和约束状态下湿模态试验,对比分析了仿真与试验结果,验证仿真模型的准确性。最后分析了沉没辊壁厚、辊长和外径对水下固有频率的影响。
2 湿模态数学模型
对于具有n 个自由度的系统,结构自由振动的动力学方程为:

式中:M—系统的质量矩阵;C—系统的阻尼矩阵;K—系统的刚度矩阵¨—对应节点的位移向量、速度向量以及加速度向量。
由式(1)可计算出系统在真空中得固有频率为:

式中:M(i)—第 i 阶广义质量;
K(i)—第 i 阶广义刚度;
fa(i)—真空中第 i 阶固有频率。
当结构处于静止的流体中,载荷向量是流体作用在结构表面(流体-结构相互作用面)的压力载荷[11]。结构表面必须考虑流体力Fu,则其动力方程修正为:

采用结构-声学模型计算沉没辊在液体中的动力特性,假设流体是均匀、无黏、无漩的理想流体,沉没辊表面的流体压力分布由声波方程确定[12]:

式中:{L}—拉普拉斯矢量;P—流体的压力矢量;c—液体中的声波速度;t—时间。
将式(4)进行离散化,进一步与结构动力方程式(3)合并可得到:

式中:带下标u 的矩阵是由流体元素生成的矩阵;带下标s 的矩阵是由结构元素生成的矩阵;下标us 的矩阵是流体与固体相互作用的耦合矩阵。
3 湿模态分析方法验证
3.1 湿模态有限元计算
采用某钢厂热镀锌线沉没辊1:8 缩比实体模型进行模态分析和试验。沉没辊模型基本尺寸参数,以及水介质试验的沉没辊在液体中的空间位置,如图1 所示。用ANSYS 有限元分析软件求解模型,该模型分为流体部分与结构部分。这里流体为水(密度ρ=1000kg/m3、粘度 μ=10-3Pa·s、声音在水中的传播速度 c=1480m/s)介质,结构的物性参数,如表1 所示。

图1 沉没辊1:8 缩比模型Fig.1 Sink Roll 1:8 Reduction Ratio Model

表1 沉没辊材料的物性参数Tab.1 Sink Roll Model Material Properties of the Parameters
有限元模型,如图2 所示。网格使用六面体单元,流体单元采用FLUID30 和结构单元采用SOLID185,共337255 个节点,43956 个单元。结构与流体接触的实体节点定义为FSI(Fluid Solid Interaction)接口。在FSI 处对网格进行加密处理,以保证两相交界面节点重合。流体的自由表面状态定义为零压力,忽略晃动效应。
自由状态下轴头两端无约束,约束状态下轴头两侧约束三个方向的位移为0。流固耦合系统动力学方程的质量矩阵和刚度矩阵为非对称矩阵,所以求解时必须使用非对称(Unsymmetric)方法。
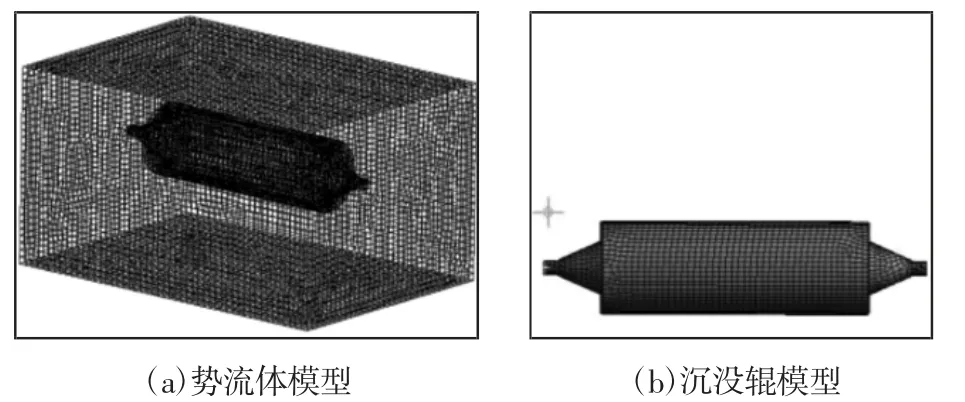
图2 沉没辊有限元模型Fig.2 Finite Element Model of Sink Roll
3.2 模态试验
试验系统主要由沉没辊、弹性绳、悬臂、水箱、试验台架、水密型加速度传感器(压电式IEPE 加速度传感器,灵敏度:99.8mV/g)、模态力锤(PCB 086C03,灵敏度:2.25mV/N)、数据采集系统(WaveBook/512)和笔记本电脑组成。系统布置及部分实物,如图3 所示。对于自由模态测试,通过弹性绳将辊模型悬挂于试验台架上;对于约束模态测试,悬臂通过螺栓固定于试验台架上,悬臂另一端与沉没辊模型的轴端固定。为保证沉没辊固有频率测量的准确性,试验台架固定在地面上且刚度足够大。将加速度传感器粘在沉没辊模型上(用A/B 胶),位于辊轴线中心截面外圆上。对于空气中模态测试,采用力锤直接激励沉没辊模型;对于水中模态测试,将用塑料薄膜密封的力锤放入水中,再敲击沉没辊模型。为了减小两种介质模态测试中力锤激励对结构产生的误差,由同一实验员尽可能保证使用同样大小作用力敲击,且本次试验采用峰值法进行模态提取[13]。进行了自由和约束状态下,沉没辊处于空气与水介质中若干组试验。
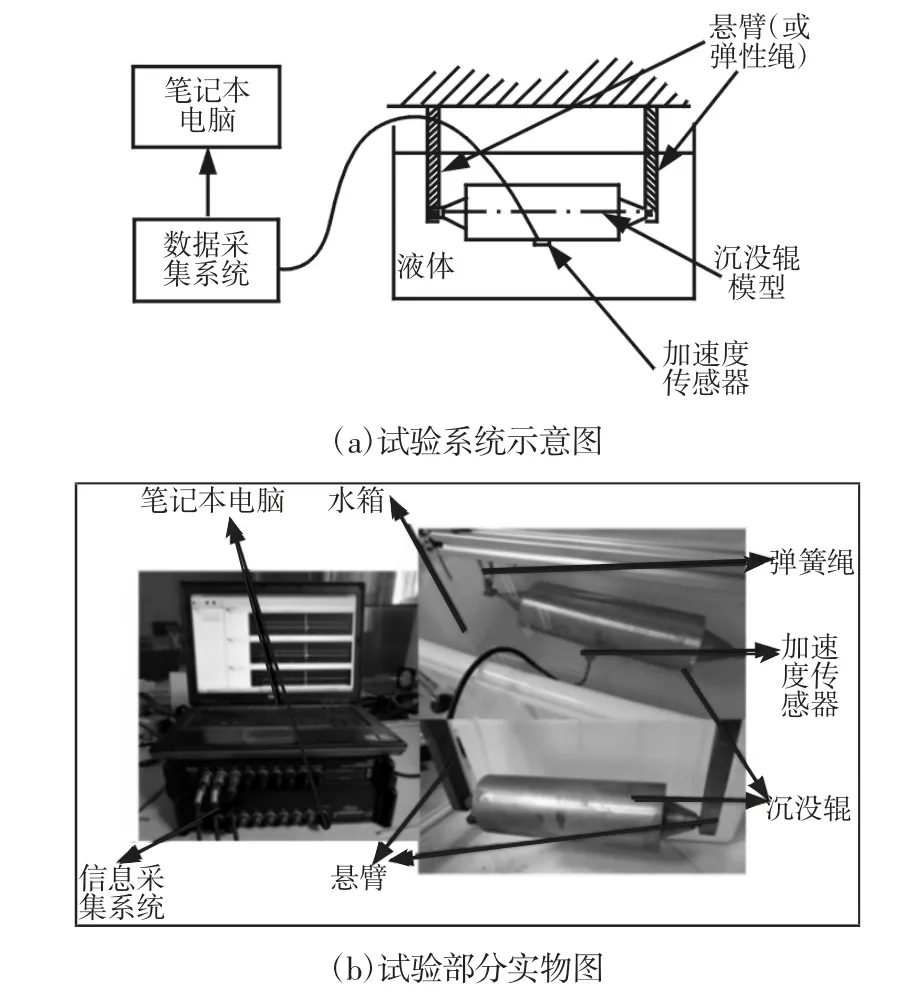
图3 沉没辊模型模态试验Fig.3 Sink Roll Model Modal Test
给出了自由状态和约束状态下,沉没辊在空气和水介质中的功率谱密度曲线,如图4、图5 所示。图4 与图5 中对比可看出,曲线各峰值点对应的频率为沉没辊的自振频率,对比水中与空气中的功率谱图可发现,水中沉没辊的自振频率和振幅相比于空气中明显降低,而且约束状态下,各峰值频率两侧的频率特征更丰富,如图5 所示。

图4 自由状态下空气与水中功率谱密度曲线Fig.4 Power Spectral Density Curve in Free State of Air and Water
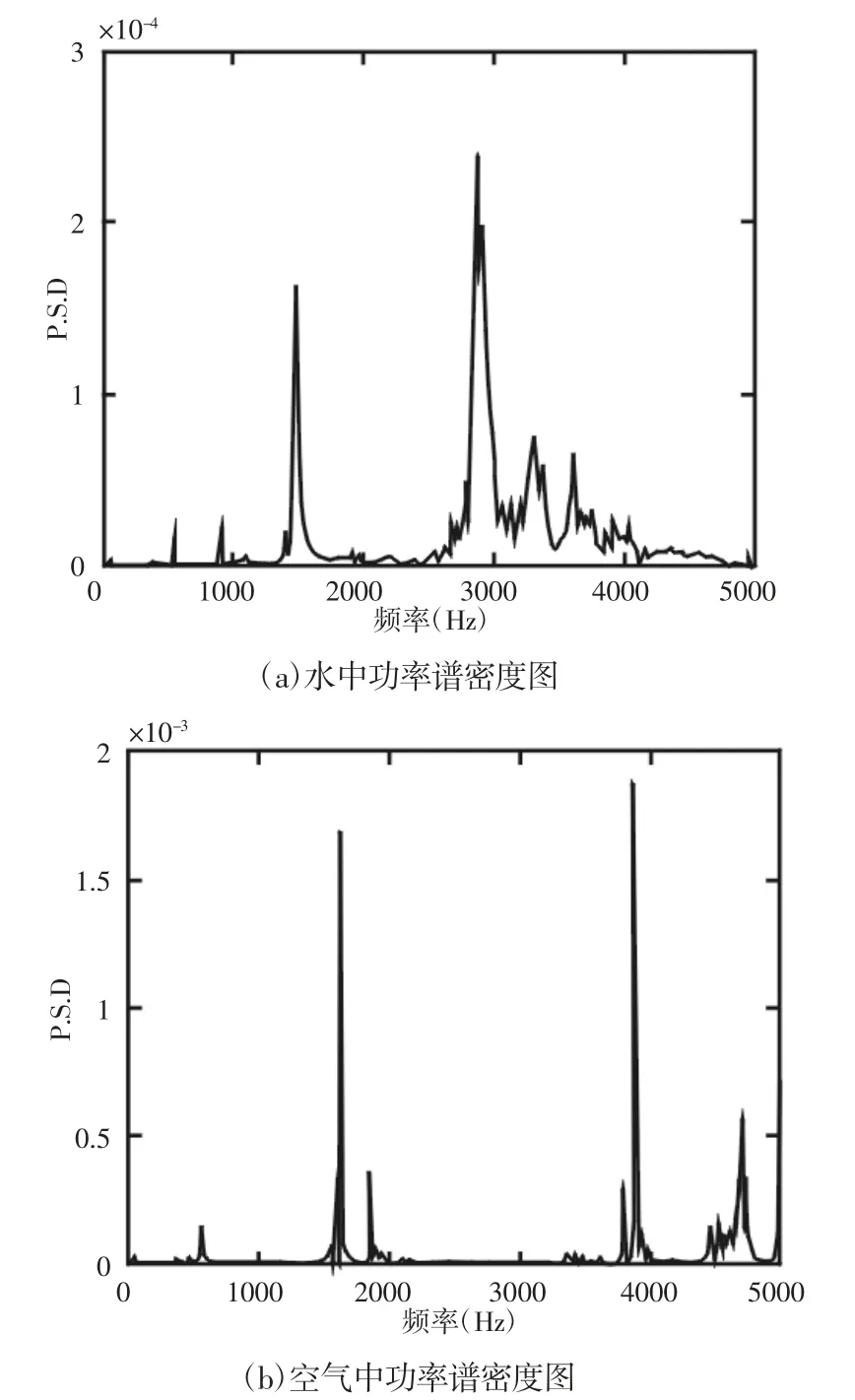
图5 约束状态下空气与水中响应时域与功率谱密度曲线Fig.5 Power Spectral Density Curve in Constraint State of Air and Water
3.3 试验与仿真结果对比
与试验相对应,建立了两种约束状态和两种介质中的仿真模型,自由状态下两种介质中均忽略前六阶固有频率为0 的刚体模态。试验与计算结果,如表2 所示。
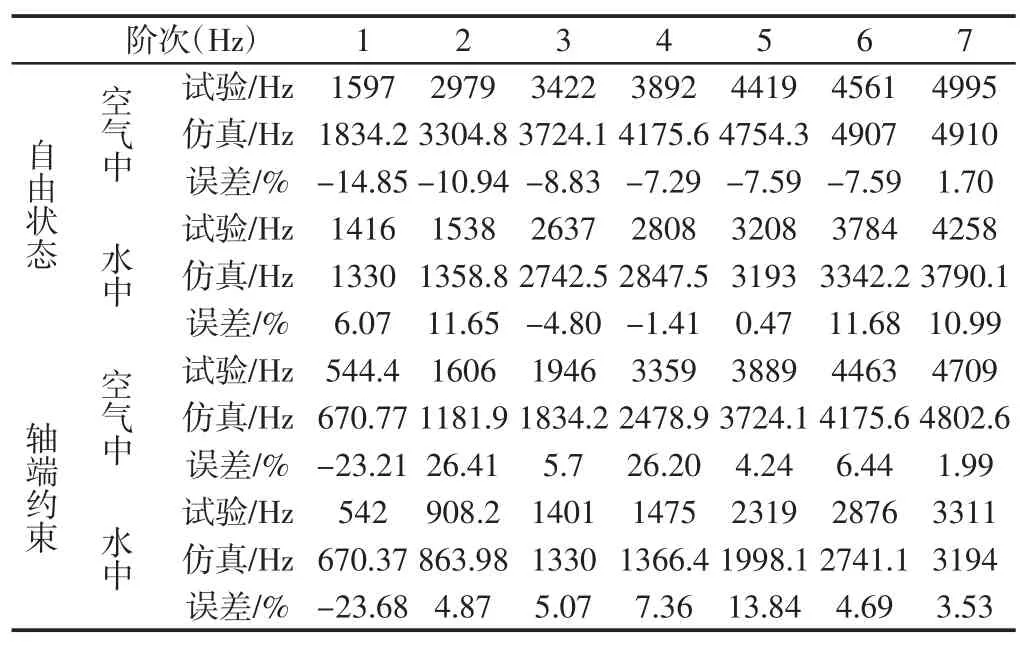
表2 沉没辊不同约束下的固有频率Tab.2 Sink Roll Natural Frequency Under Different Constraints
由于峰值法的局限性,对于轴对称结构的重根模态无法识别[14],因此本次试验与仿真不考虑其重根模态。对比两种状态的相应各阶模态,水介质中试验与仿真的固有频率均低于空气中,且不同阶次的固有频率的降幅相差较大。在自由状态下,仿真与试验的相对误差小于15%,最大相对误差出现在空气介质中第1阶模态,频率误差为14.85%,最小相对误差在水介质中第5 阶模态,频率误差为0.47%。在约束状态下,最大相对误差出现在空气介质中第2 阶模态达到26.41%。最小相对误差在空气介质中第7 阶模态,频率误差为1.99%。仿真计算结果与试验结果整体吻合度较高,验证了有限元模型的准确性。
4 结果与讨论
4.1 约束方式对沉没辊湿模态的影响
表2 水介质中两组约束仿真与对应试验的各阶频率值,如图6 所示。由图6 和表2 可看出,根据仿真计算结果可知,自由状态下的第1、3、5 阶模态频率值与轴端约束下的第3、6、7 阶频率值几无差异;根据试验结果可知,自由状态下的第1、3、5 阶模态频率实测值与轴端约束下的第3、6、7 阶频率值的差异率分别为1.1%、8.3%和3.1%。进一步根据水介质中两组仿真结果可知,自由状态下的第1、3、5 阶与轴端约束下的第 3、6、7 阶振型也相同。这3 种模态振型可用轴向半波数m 与周向波数n 来表示,如图6 所示。对于沉没辊模型在水介质中的两种约束条件下,其振型分别为(1,2)、(2,2)和(1,3),相应振动方式为辊身径向振动不同、两轴端无相对位移。故这3种模态的固有频率和振型与轴端约束无关;而其他振型包括辊的弯曲、扭转等均受轴端约束的影响。为进一步深入讨论与沉没辊轴端约束无关的湿模态固有频率影响因素,因此仅从振型(1,2)、(2,2)和(1,3)进行结构外形尺寸对其固有频率的影响研究。

图6 水中两种状态下的各阶频率对比Fig.6 Two States Under Each Order of Frequency Comparison in Water
4.2 沉没辊湿模态影响因素分析
4.2.1 壁厚对湿模态的影响
建立外径100mm,辊身长287.5mm,壁厚分别为2.5mm、5mm、7.5mm、10 和12.5mm 的5 种沉没辊模型,对其进行有限元湿模态计算,所得结果,如图7 所示。

图7 不同壁厚对固有频率的影响Fig.7 Different Wall Thickness of the Natural Frequency
由图7 可看出,同一振型下,随着沉没辊的壁厚增加,固有频率值会增大,且呈线性变化。不同振型的变化率有所不同,振型(1,3)的斜率最大。
4.2.2 辊身长对湿模态的影响
建立外径100mm,壁厚5mm,辊身长分别为275mm、325mm、375mm、425mm 和475mm 的5 种沉没辊模型,对其进行有限元湿模态计算,所得结果,如图8 所示。

图8 不同辊身长对固有频率的影响Fig.8 Different Roll Body Length of the Natural Frequency
由图8 可看出,同一振型下,随着沉没辊的辊身长度增加,固有频率值会降低。不同振型的变化率有所不同,振型(2,2)的降幅最大,说明辊身长对该振型的影响最大。
4.2.3 外径对湿模态的影响
建立壁厚为5mm,辊身长为287.5mm,外径分别为100mm、105mm、110mm、115mm、120mm 的 5 种沉没辊模型,对其进行有限元湿模态计算,所得结果,如图9 所示。
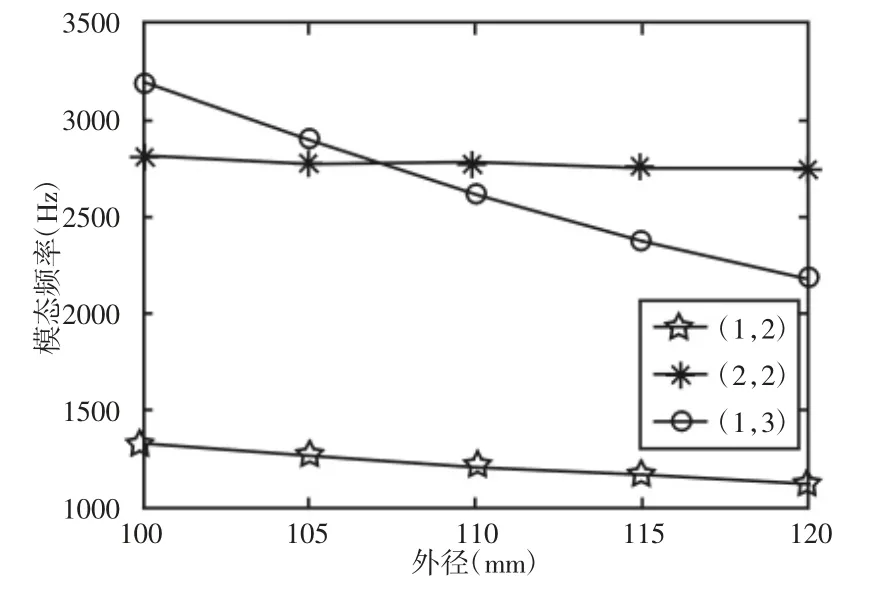
图9 不同外径对固有频率的影响Fig.9 Different Outer Diameter of the Natural Frequency
由图9 可看出,同一振型下,随着沉没辊的外径增加,固有频率值会降低。不同振型的变化率有所不同,振型(1,3)的降幅最大,说明外径对该振型的影响最大;外径对振型(2,2)几乎无影响。
5 结论
以试验与仿真结合的方法研究沉没辊在不同介质和不同约束下的固有频率变化,研究结果如下。
(1)相比于空气中,沉没辊模型浸没水中各阶模态频率会降低,但不同阶次的固有频率的降幅相差较大。
(2)在水介质中,随着壁厚增加,固有频率值呈线性增长;随着辊身长度和外径的增加,各阶固有频率值均会降低,辊身长变化对振型(2,2)的影响最大,外径变化对振型(1,3)影响最大、对振型(2,2)基本无影响。
对于两种约束条件和两种介质的沉没辊,前7 阶共振频率仿真计算结果与试验结果整体吻合度较高,仿真计算的模型合理,分析结果准确。研究结果对沉没辊类似结构的设计和振动控制具有指导意义和参考价值。
