剃齿过程中重合度对啮合接触特性的影响
2020-08-17蔡安江李文博刘立博
蔡安江,耿 晨,李文博,刘立博
(西安建筑科技大学机电工程学院,陕西 西安 710055)
1 引言
一般认为,重合度是引起剃齿齿形中凹误差的重要因素。在剃齿过程中,剃齿刀和工件齿轮的啮合瞬时为点接触,而实际重合度往往不是整数,工件齿轮在节圆附近啮合时,其接触点数会发生突变,左右啮合线上接触不平衡,使得作用在齿轮齿面的切削力增大,齿面材料去除过多,最终会形成较为明显的齿形中凹误差[1]。
文献[2-4]将LTCA 技术应用于修形斜齿轮,推导了弧齿锥齿轮承载齿面接触分析,给出了包含误差的修形斜齿轮在不同受力条件下的齿面载荷分布和传动误差。文献[5]将机床运动几何误差及安装误差考虑到模型中,提出ETCA 方法,得到机床运动误差和安装误差对齿面加工质量影响的定量关系。针对剃齿啮合的接触问题,文献[1]推导出了剃齿过程中的不同啮合状态分区,并计算出接触点的应力应变。但是其并未考虑剃齿刀齿面上容屑槽和切削刃的存在。
以Hertz 理论和齿轮加工原理为基础,提出了剃齿过程中的齿面接触分析方法,分析了不同重合度下的剃齿啮合接触特性曲线,研究了重合度对剃齿齿形中凹误差的定量影响。
2 剃齿啮合模型
2.1 剃齿啮合
剃齿加工是应用最广泛的齿面精加工方法之一,可以提高齿面成形质量。剃齿啮合中,当啮合落到容屑槽两端的切削刃上时,剃齿刀和工件齿轮上接触点的法向速度v1n、v2n不相等,切削刃切入工件齿轮齿面;同时,剃齿刀和工件齿轮的切向速度v1t、v2t也不相等,齿面间存在相对滑移,形成剃削行为,相对速度-v2t即为剃削速度。工件齿轮轴向往复运动,最终将被剃齿面完整剃削。在建立剃齿刀和工件齿轮的剃齿啮合接触模型时,首先建立二者的空间啮合关系,如图1 所示。
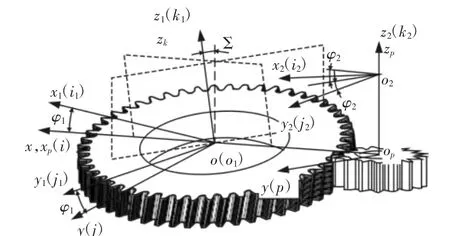
图1 剃齿啮合几何模型Fig.1 Geometric Model of Gear Shaving
2.2 数学模型
2.2.1 剃齿刀齿面方程
不同于螺旋斜齿轮,剃齿刀齿面上按规律排列着多条容屑槽和切削刃,对工件齿轮齿面作切削加工。在计算出剃齿刀的基本参数的基础上,容屑槽的参数依照国家标准(GB/T14333-2008)选择,可以将其视为已知。
在剃齿刀齿面上,容屑槽是等距分布的。在O1X1Y1Z1坐标系中,剃齿刀的右齿面方程可以表示为:

式中:rb1—剃齿刀基圆半径;
u1—参变数,表示渐开线上该点处压力角和展角的和;
p1—剃齿刀齿面的螺旋参数,p1=rb1cotβb1;
βb1—剃齿刀基圆螺旋角;
β—剃齿刀分度圆螺旋角;
λ1—参变数,表示渐开线齿廓从起始处沿着螺旋线,绕Z 轴转过的角度;
b1、L、k—剃齿刀容屑槽参数。
2.2.2 剃齿啮合方程
剃齿啮合过程符合经典啮合原理,在啮合点处满足啮合方程:

式中:v(12)—两齿面在啮合点处的相对运动速度;n—两齿面在啮合点处的法线矢量。
根据微分几何分别求得 v(12)、n,代入式(2)可得:
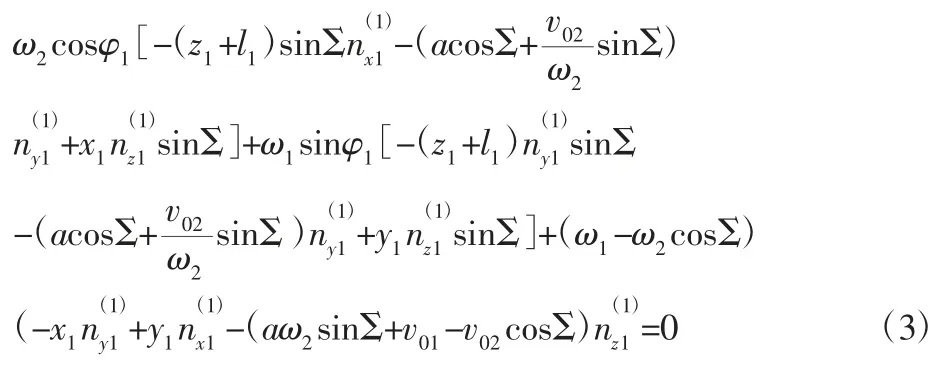
剃齿过程为双自由度啮合,所以得到的啮合面方程式为:

由于剃齿啮合为交错轴斜齿轮啮合,啮合过程为点接触,这是为了增大剃齿啮合过程中的表面接触应力,增强剃齿切削效果。可得其啮合线方程为:
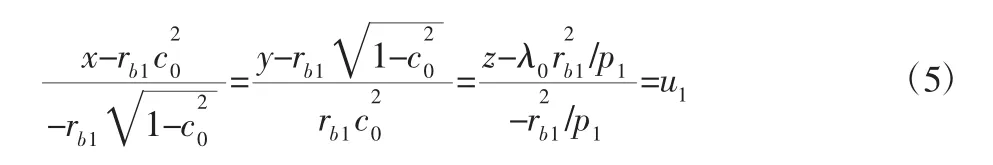
其中,c0=cos(u1-λ1-φ1),可证其为常数。
2.2.3 工件齿轮齿面方程
剃齿啮合过程是一个连续的切削过程,但是为了方便建立时变的工件齿轮齿面方程,我们将剃齿刀的径向进给离散化,这样可以计算得到剃齿啮合过程中的时变中心距,并给出剃齿刀每转过一圈,切削得到的工件齿轮齿面方程。剃齿啮合中心距为:

式中:fr—剃齿刀的径向进给速度;n—剃齿刀的转速;N=0,1,2,3……。
剃削得到的工件齿轮齿面和剃齿刀齿面,满足无侧隙啮合条件。建立工件齿轮时变齿面模型,工件齿轮齿廓,如图2 所示。
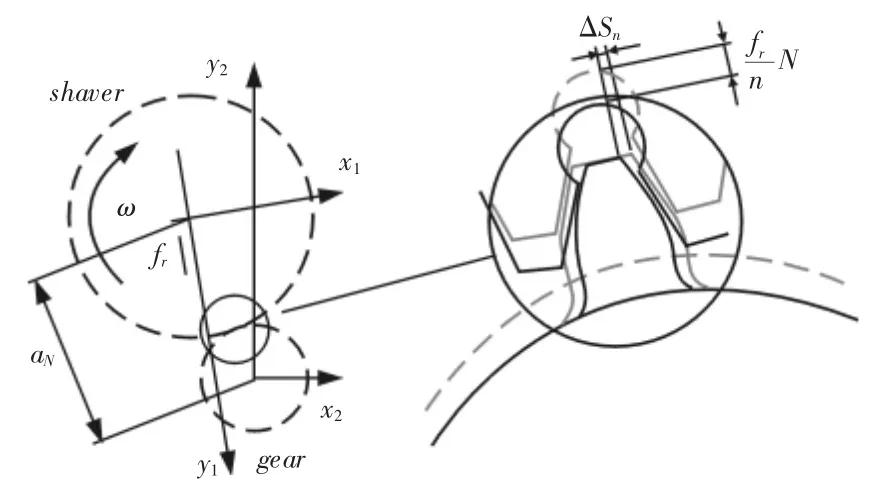
图2 工件齿轮齿廓Fig.2 Tooth Profile of Workpiece
在坐标系S2中,工件齿轮齿面的参数方程可以表示为:

式中:l2—工件齿轮轴向进给的距离;Σ—剃齿刀和工件齿轮的轴交角。
在式(7)中,λ0为常数。
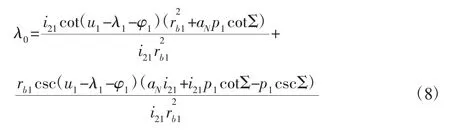
3 剃齿啮合接触特性分析
3.1 剃齿啮合接触特性
剃齿啮合接触特性主要研究剃齿刀和工件齿轮齿面间的接触应力和变形,包括法向接触力fn、接触应力σH、接触变形δE。剃齿啮合过程中,工件齿轮同时受到齿面接触应力和弯曲应力的作用,而轮齿弯曲变形对齿面影响较小,故不予考虑。
3.2 重合度
重合度表示在齿轮啮合过程中同时参与啮合的轮齿对数的多少[6],渐开螺旋面的交错轴啮合为点接触,啮合齿轮对的端面重合度、纵向重合度以及总重合度是同一个值,故剃齿啮合的重合度为[7]:

式中:l—端面有效啮合线长度;
Δl—剃齿时齿轮端面有效啮合线超越量。
当重合度不同时,剃齿刀的齿顶圆、齿廓的曲率半径等都会发生变化,剃齿啮合状态也会发生改变,剃齿啮合的最大法向接触力将随之发生改变。
3.3 剃齿啮合接触分析算法
剃齿刀齿面的啮合迹线是不连续的,容屑槽处的啮合点实际落在其两端的切削刃上,接触点的曲率半径发生变化,法向力也会改变,进而影响金属切削,并对中凹误差产生影响。
3.3.1 齿廓啮合点
在图1 坐标系Sp中,选择工件齿轮端面所在平面,即二维坐标系OP-xpyp,剃齿刀的基圆在此坐标系中的投影为椭圆,且方程可以给出:

工件齿轮基圆方程已知,可以给出当前中心距下工件齿轮端面上的啮合线方程。由于剃齿啮合对重合度的变化量很小,为了简化计算,取中心距为设计中心距。
通过坐标变换将式(7)转换为坐标系Sp中的工件齿轮齿面方程,再投影到平面oPxPyP上,得到工件齿轮的端面齿廓。在剃齿过程中,工件齿轮随着剃齿刀不断转动,所以齿面方程也应该不断更新,工件齿轮齿面方程可以通过坐标变换得到:

式中:Mp2—坐标系 S2到坐标系 Sp的变换矩阵;tp=t2=[0 0 0 1]。
将工件齿轮的齿面方程投影到oPxPyP面上,得到工件齿轮的齿廓方程,将其与啮合线方程联立解得啮合点。
3.3.2 求解法向作用力、应力和应变
根据上述数学模型,建立轴向剃齿啮合过程中的力学模型,并对所建的力学模型进行齿面载荷接触分析。
在两点和三点啮合时,运用静力学方程可以解得各接触点的法向力,不再赘述。
在四点接触区域,系统保持平衡状态 F1,F2,F3,F4未知,通过力和力矩的平衡方程不足以解出法向作用力的大小,需建立四个方程来求解,此时引入协调方程:

式中:F—各接触点的法向作用力;
b—各接触点接触椭圆的长轴长。
协调方程的含义为两条啮合线上的接触变形之和相等。
在获得接触力后,根据斜齿轮齿面接触应力求解方法,求解各啮合接触点的应力[8]:
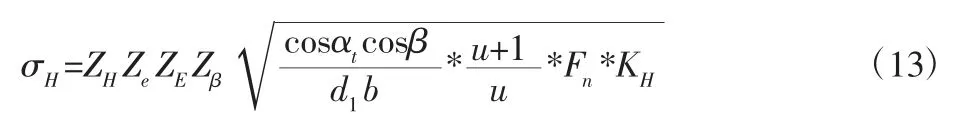
式中:u—剃齿啮合的传动比;Fn—啮合点的法向作用力;ZH、Ze、ZE、Zβ—啮合对的相关系数,可查表得到;实际载荷系数KH=KAKVKHαKHβ。
啮合点接触变形的求解,适用弹性圆柱体接触变形的计算公式:

式中:E—工件齿轮的弹性模量;
v—工件齿轮的泊松比;
L—工件齿轮齿宽;
b—接触椭圆半长轴。
3.4 剃齿啮合接触特性计算
由于剃齿齿形中凹误差大都发生在重合度小于2 的剃齿啮合加工中,基于文献[7]中剃齿刀设计的原理与方法,根据工件齿轮的参数设计4 把剃齿刀,材料属性,如表1 所示。设计参数,如表2 所示。
将四把剃齿刀分别与工件齿轮啮合,建立四组不同的剃齿啮合模型,剃齿过程的剃削力主要由径向进给量确定[9],不同的径向力会对剃齿造成不同的剃削变形。经剃齿啮合接触分析可得,法向接触力、接触应力以及齿廓的变形量的变化曲线,如图3 所示。四组剃齿啮合模型接触点数的周期性变化规律均为3-4-3-2-3-4。
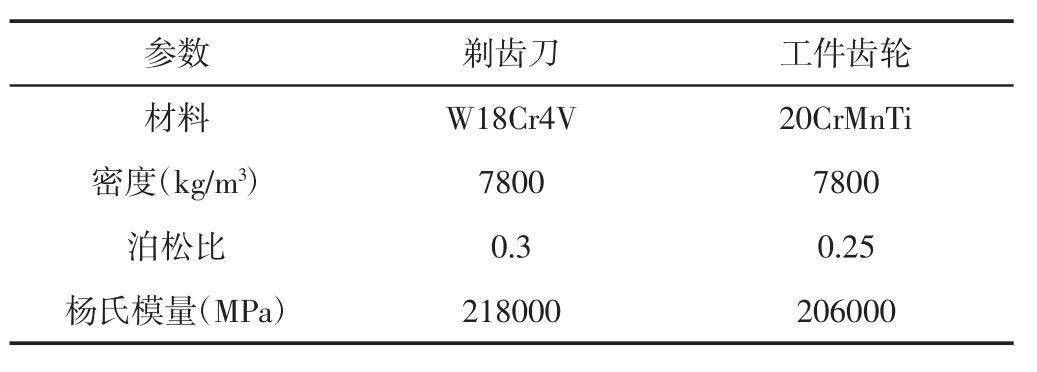
表1 工件齿轮材料的基本参数Tab.1 Basic Material Parameters of Workpiece

表2 剃齿刀的基本设计参数Tab.2 Basic Design Parameters of Shaving Cutter
图3 表明:齿面上法向接触力、接触应力和变形量均表现出明显的阶跃特性,是因为啮合状态发生改变,接触点数的突变导致径向力的阶跃。DE 段为两点接触,在径向力不变的情况下,齿面接触点所承受的法向接触力和齿面变形量都会增大。CD 段为三点接触,这一段齿廓的受力和变形,与DE 段基本相同,是因为虽然接触点多,但是单点接触受力不平衡,所以更容易出现塑性形变。图3(a)~图(b)中接触应力与应变变化趋势大致相同,且值也相差不大,表明当重合度足够大时,再继续增大对齿面接触应力影响不大,反而会使得剃齿中心距减小,容易造成沉割、根切等不良影响。比较四个不同重合度的分析结果,可以看出,重合度越小的剃齿啮合模型,其在节圆附近齿面的法向接触力、接触应力以及变形量都越大,相对也更容易产生塑性形变,随着误差不断复映,最终会在齿面节圆附近呈现出明显的齿形“中凹”误差。
4 仿真验证
4.1 有限元仿真前处理
由于刀齿过渡曲线等复杂曲面的存在,在ABAQUS 中进行前处理有可能会存在很小的尖角,而Hypermesh 可以对单元节点进行适当修改,故应用Hypermesh 进行剃齿啮合分析模型的网格划分。减缩积分对网格的扭曲变形不敏感,对位移的求解精度及速度也较为优越[10]。Celik 验证比较了局部模型代替整体模型可以满足工程应用[11]。为更合理地获取齿廓任意曲率半径的应力值,需对分析步、相互作用和载荷进行设置:(1)分析步设置为[Dynamic,Explicit],剃齿啮合为典型的多体转动问题,应设置Nigeom 为On。为了避免出现模型单元变形速度和膨胀波速比超过1 等错误,设置时间缩放系数为0.5;(2)在剃齿刀部件上施加刚体约束;(3)载荷模块设置刀齿啮合边界条件,且在剃齿刀上施加200r/min 的角速度。
4.2 数据对比
根据表2 所示的四组剃齿啮合模型,分别建立有限元模型,剃齿啮合接触仿真结果,如图4 所示。结果表明:不同啮合状态下接触应力存在明显的变化,同时,在开始啮入时,接触应力的初始值明显小于剃齿啮合接触特性理论计算结果,原因是在啮入和啮合状态发生变化时,接触应力的变化需要一个达到稳态的过程。比较图4 四组剃齿啮合模型的应力曲线可知,轮齿中部节圆附近区域应力趋于稳定,该区域主要是三点啮合区,取应力的平均值为此处应力值,分别为 618.076N,622.400N,665.865N,681.963N。可见,随着剃齿啮合重合度的减小,加工啮合过程中的最大应力值随之非线性增大。使用有限元法计算所得最大应力均大于剃齿啮合接触特性分析的计算结果,其偏差分别为9.539%,8.775%,7.308%,0.268%,满足工程实践需求。
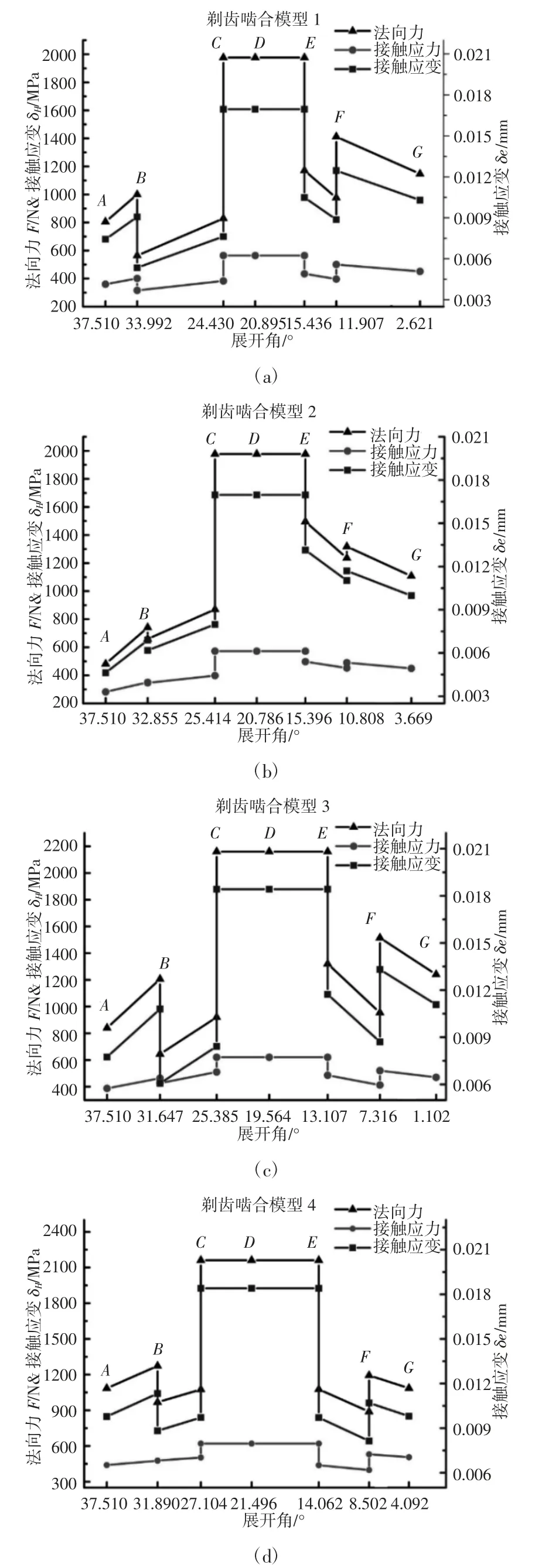
图3 不同重合度的剃齿啮合接触特性曲线Fig.3 Shaving Contact Characteristic Curves with Different Contact Ratios

图4 不同重合度的剃齿啮合接触特性仿真曲线Fig.4 Simulation Curves of Shaving Contact Characteristic with Different Contact Ratios
5 结论
针对剃齿啮合过程中的接触特性,考虑剃齿刀齿轮容屑槽和切削刃的存在,提出剃齿啮合接触特性分析方法,并通过有限元仿真验证理论研究,主要结论如下:
(1)剃齿啮合接触分析表明剃齿啮合重合度越低,出现在节圆附近的三点啮合区域的法向接触力的最大值越大,此处的剃削量和形变也越大,更易产生剃齿齿形“中凹”误差。
(2)在剃齿啮合中,并不是重合度越大越好。当重合度足够大时,继续增大重合度影响剃齿啮合接触性能很小。反而会因为重合度过大,发生沉割、根切现象。
(3)通过有限元计算得出,节圆附近区域啮合接触应力趋于平稳。节圆附近三点啮合区域出现剃齿啮合接触应力的最大值。有限元法计算得出的应力最大值比剃齿啮合接触分析方法所得结果偏大,处于误差范围内。
