基于支持向量回归的PV/T 组件温度实时预测

2020-08-17李畸勇汤允凤周兴操谢玲玲宋春宁

可再生能源 2020年8期

李畸勇，汤允凤，胡恒，陈敏，周兴操，谢玲玲，宋春宁

（1.广西大学电气工程学院，广西南宁 530004； 2.广西大学广西电力系统最优化与节能技术重点实验室，广西南宁 530004）

0 引言

通常情况下，光伏（PV）组件的转换效率约为15%。在标准状况（环境温度为25 ℃，太阳辐照度为1 000 W/m2）下，PV 组件温度每升高1 ℃，发电效率约下降4‰[1]。为了解决温度对PV 组件的影响，研究人员设计了一种以水或空气为工质的平板型光伏光热（PV/T）综合利用系统，从而降低了PV 组件温度，提高了PV 组件发电效率，并且回收了工质热量[2]。PV/T 组件的温度具有非线性、时变性以及分布复杂的特点，只有掌握PV/T 组件温度的变化情况，才能进一步开展优化控制，因此，准确预测PV/T 组件温度具有重要意义。

目前，PV/T 组件温度预测模型主要包括物理模型、时间序列模型和人工智能模型[3]～[6]。其中，物理模型是根据能量平衡原理构建的热性能数学模型，该模型经过复杂的数值计算能够得到PV/T组件温度。但由于各影响因子在系统运行过程中均不断变化，所建立的数学模型对随机变化的变量适应性不高，导致该模型温度实时预测效果不理想。时间序列模型为根据PV/T 组件历史时间序列温度数据建立的模型，通过分析过去温度的变化趋势对当前或未来短期温度进行预测，因此，时间序列模型更适用于运行状态平稳、规律性较强的系统。由于PV/T 组件温度具有非线性和非平稳性，因此，利用时间序列模型进行模拟时，会存在预测精度不高的问题。

人工智能模型能够将智能算法应用到PV 组件温度预测的过程中。目前，大多数人工智能模型均采用传统的神经网络智能算法来预测光伏组件温度。文献[5]中使用BP 神经网络对光伏阵列温度进行预测，由于只考虑了环境温度和光伏组件输出功率对光伏组件温度的影响，因此，当太阳辐照度较大时，预测结果会存在较大的误差。文献[6]利用Elman 神经网络对PV/T 组件的温度进行了预测，由于只考虑了气象因素对光伏组件温度的影响，因此，预测结果仍存在较大的误差。

针对以上不足，本文以水冷式平板型太阳能集热器为研究对象，将外界气象环境因子、冷却水流速和PV/T 组件进、出口温度作为影响PV/T 组件温度的主要因素，建立了基于支持向量回归（SVR）算法的温度预测模型（以下简称为SVR 温度预测模型），对PV/T 组件温度进行实时预测。与传统的神经网络算法相比，SVR 算法可以避免局部最优问题，对小样本、非线性、高维的回归预测问题有较强的泛化能力[7]。由于原始数据变量较多且差异较大，本文在建立预测模型之前，采用了归一化方法，对数据进行预处理。同时，为了避免参数设置不合理引起的过拟合和欠拟合问题，采用了网格搜索与交叉验证相结合的方法，对SVR温度预测模型进行参数寻优，进而提高了该模型的预测精度。最后，通过PV/T 系统实验平台对SVR 温度预测模型的预测结果进行验证。分析结果表明，优化后的SVR 温度预测模型的预测精度更高，泛化能力更强，可以在水泵运行情况下，实时预测PV/T 组件的温度。

1 PV/T 实验平台介绍

图1 为水冷式平板型PV/T 组件结构图。

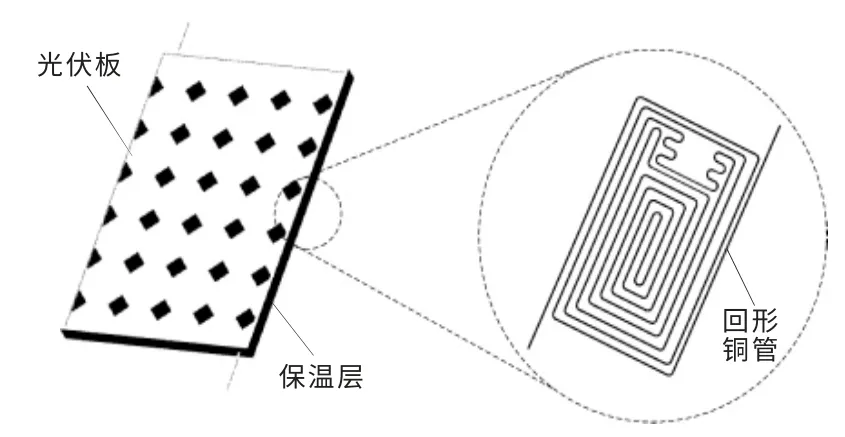
图1 水冷式平板型PV/T 组件结构图Fig.1 Water-cooled flat PV/T module structure diagram

由图1 可知，水冷式平板型PV/T 组件主要由光伏板、回形铜管、保温层组成。当PV 组件吸收太阳辐射能后，热量会传递到光伏组件背面上回形铜管中的冷水。回形铜管的设置，不仅使电池组件温度均匀，还增大了流体的接触面积，增强了降温效果。

图2 为PV/T 系统结构图。

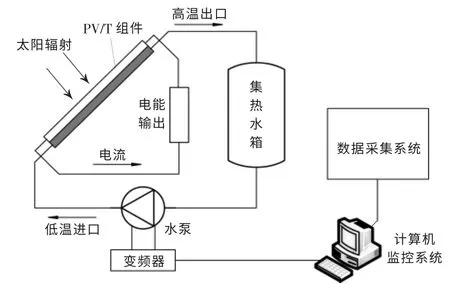
图2 PV/T 系统结构图Fig.2 PV/T system structure diagram

由图2 可知，PV/T 系统主要包括PV/T 组件、水泵、变频器、数据采集系统、计算机监控系统。其中，数据采集系统包括了校园气象站、温度传感器、流量计等，可采集PV/T 系统的各项数据。水泵频率可以根据PV/T 组件温度情况进行手动控制或者由MATLAB 生成控制算法进行自动控制，使得光伏组件能够在适宜的温度环境下工作，既提高了发电效率，又能够实现热量回收。

2 SVR 温度预测模型建立

2.1 PV/T 组件温度影响因数的选取

本文实验平台位于广西南宁（108.3°E，22.8°N），PV/T 组件安装倾角为22°，朝向为正南方向。影响PV/T 组件温度的各气象因素数据由校园气象站采集，具体参数包括环境温度Ta、太阳辐照度E、环境湿度Ha、风速Ws和风向Wd。此外，通过上位机采集流量传感器和温度传感器的测试结果，具体包括循环水流量Vm，PV/T 组件的进口水温Tin、出口水温Tout以及PV/T 组件温度TPV。其中，PV/T 组件温度为均匀安装在PV/T 组件背面上的8 个温度传感器测量值的平均值。

本文选取环境温度、太阳辐照度、环境湿度、风速、风向、循环水流量、PV/T 组件进口水温和出口水温8 个变量作为模型的输入变量，PV/T 组件温度为模型的输出变量。预测过程中，先基于训练集数据建立模型，再利用测试集数据仿真测试模型的性能参数，把满足预测指标的模型用于PV/T组件温度的实时预测。

图3 为SVR 温度预测模型的建立过程及其实时预测流程。

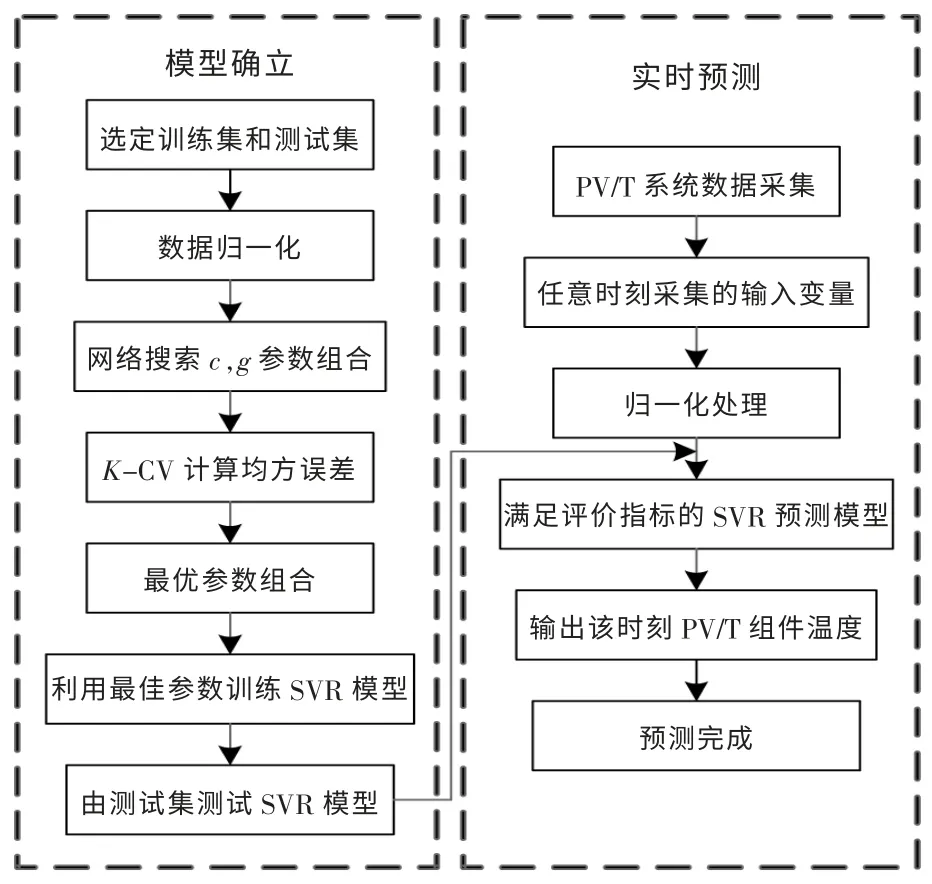
图3 SVR 温度预测模型的建立过程及其实时预测流程Fig.3 SVR temperature prediction model establishment process and its real-time prediction process

2.2 支持向量回归（SVR）基本原理

支持向量机（SVM）包含分类型支持向量机和回归型支持向量机[8]。本文建立了PV/T 组件温度的回归预测模型，因此，使用了回归型支持向量机（SVR）。在回归型支持向量机中引入了不敏感损失函数ε，若真实值和预测值之间的绝对差值不大于ε，则损失值（预测值与真实值之间的偏离）为0。

若使用l 组样本训练模型，则样本数据集合为{（x1，y1），（x2，y2）…（xi，yi）…（xl，yl）}。其中，xi为第i 个训练样本的输入列向量。本实验模型有8个输入变量，1 个输出变量，则xi=[xi1，xi2，…，xi8]T，yi为相应的输出变量（真实值）。令SVR 温度预测模型的线性回归函数T（x）为

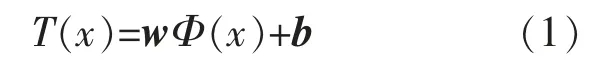
式中：w 为权值向量；Φ（x）为非线性映射函数；b为偏置向量。

由于PV/T 组件温度存在不确定性，引入松弛变量ξi，ξi*，则优化SVR 温度模型的表达式为

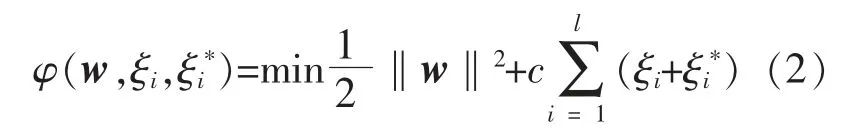
式中：c为惩罚因子，表征模型训练温度误差大于ε 时，样本惩罚的大小。

在式（2）中引入Largrange 函数后，将其转换为对偶形式并求解，可得到式（2）的最优解为α=[α1，α2，…，αl]，α*=[α1*，α2*，…，αl*]。于是，回归函数转换为

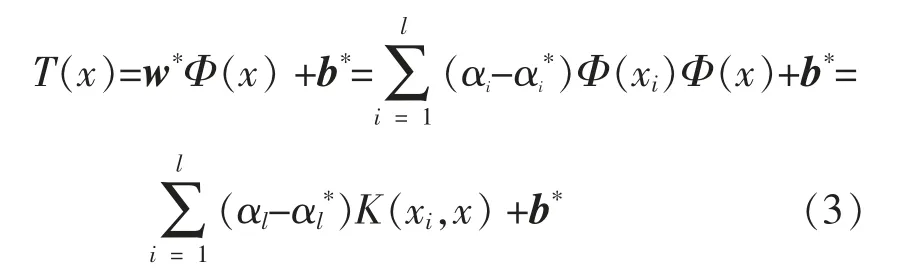
在SVR 温度预测模型中，核函数K（xi，x）的类型对模型的性能影响较大，可以通过比较不同核函数的性能情况来选择最佳的核函数类型。常见的核函数类型有线性核函数、多项式核函数、径向基（RBF）核函数和Sigmoid 核函数。

图4 为SVR 结构图。由图4 可知，当输入变量为l 组样本集时，经过中间节点线性组合后，输出了回归预测的目标变量。

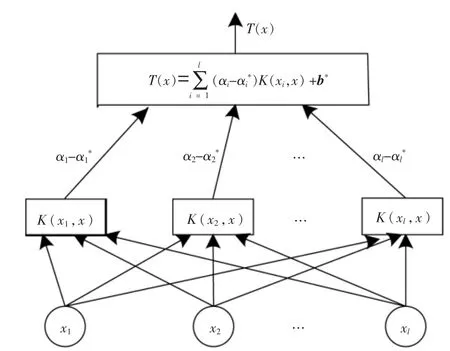
图4 SVR 的结构图Fig.4 SVR structure diagram

2.3 基于网格搜索和交叉验证的SVR 参数优化

由SVR 原理可知，惩罚参数c 和核函数参数g 对SVR 温度预测模型的计算性能有很大影响，因此，寻找最优的惩罚参数和核函数参数具有重要意义。

网格搜索是对参数值的一种穷举搜索方法，将c 和g 组成的所有参数组合构成的空间进行合理地网格划分，可以遍历所有网格交叉点处的参数组合。由于模型输入变量之间存在相关性，虽然启发式算法中的遗传算法（GA）和粒子群算法（PSO）收敛速度较快，但容易陷入局部最优，因此，利用网格搜索的遍历性找出全局最优解，更具有可靠性和实用性[9]。

常见的交叉验证法包括重复随机抽样法、留一法和K-fold 交叉验证法等[10]。其中，随机抽样法仅须要把原始数据随机地分成两组进行训练和验证，虽然这样处理过程简单，但模拟结果的精确度却与随机分组的情况有很大关系，故而可靠性不高；留一法则存在计算成本高，收敛速度慢的缺点；采用K-fold 交叉验证（K-CV）法，能够有效地避免模型在训练过程中过拟合和欠拟合状态的发生，从而提高了模型的泛化能力。

基于上述分析，本文使用网格搜索和K-fold交叉验证相结合的方法对SVR 温度预测模型进行参数寻优。该模型的参数选取步骤如下。

①建立网格坐标。网格坐标的范围决定了参数寻优的范围，为保证寻优范围足够广，本文采用指数函数对网格进行划分。令a=（-m，m），b=（-n，n），则模型参数网格点坐标为（c，g）=（2a，2b）。

②划分样本。利用K-fold 交叉验证法时，将原始样本均分成K 组，每组轮流作为验证集，测试其他K-1 组训练得到的模型。

③确定预测误差。取上述K 次测试结果的均方误差的平均值作为本次模型的性能指标。

④确定最优参数组合。网格上所有交叉点处的参数组合经过K-fold 交叉验证后，均方误差（CVmse）最小值所对应的参数组合就是模型的最优参数。

本文把网格搜索和K-fold 交叉验证相结合，不仅可以找出全局的最优解，还能够有效地避免拟合不当的影响，从而提高了整个模型的预测精度。

3 仿真算例分析

3.1 数据样本选取与数据归一化处理

本文由校园气象站和上位机搭建的PV/T 综合利用监控系统进行数据采集，每1 min 采集一次。由于夏季PV/T 组件受环境温度的影响最为显著，因此，选取2017 年6 月1 日-8 月15 日（非阴雨天）的数据作为训练模型的样本，选取2017年8 月16 日-9 月1 日（非阴雨天）的数据用来检验该模型的预测精度。

在SVR 温度预测模型的输入变量中，环境温度、太阳辐照度、环境湿度、风速、风向以及PV/T组件出口温度均为不可控因素，循环水流量和PV/T 组件进口温度均为可控因素，因此，在PV/T系统的运行过程中，为了使样本数据具有多样性，当PV/T 组件达到一定温度时，开启水泵并使其在不同的频率下运行一段时间，同时，改变集热水箱的温度，这样循环水流量和PV/T 组件进口温度的数据就会呈现出多样性，使得训练出来的模型更具有普适性。

由于影响PV/T 组件温度的变量较多，这些变量不仅量纲不同，而且数据大小存在明显差异，因此，在建立预测模型之前，应先对数据进行归一化处理。常用的归一化方法包括最值归一化（Min-max Normalization）法和中值归一化（Median Normalization）法。

采用最值归一化法时，通过对原始样本数据进行线性变换，使原始数据映射到[0，1]内，最值归一化法的转换函数为

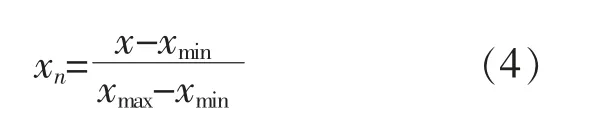
式中：xn为归一化后的数据；x 为原始数据；xmin为x 的最小值；xmax为x 的最大值。

采用中值归一化法时，将原始数据中最大值与最小值之间的差值作为中值的比例因子，将原始数据转化到某一区间，以零点作为该区间的中值，该区间设定为[-1，1]。中值归一化法的转换函数为

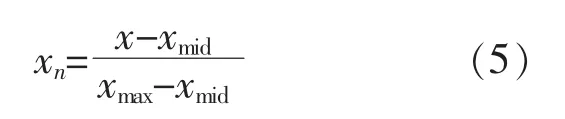
3.2 预测精度评价标准

SVR 温度预测模型的评价指标包括相对误差E、均方误差MSE 和平方相关系数R2。其中，E表征温度预测的准确程度；MSE 表征温度预测过程中预测结果的稳定性和波动性；R2表征温度预测值与真实值之间的关系。 E，MSE 和R2的计算式分别为

式中：l 为样本量；T（xi）为预测值。

当SVR 温度预测模型的E，MSE 越小，R2越接近于1 时，则该模型的预测精度越高。

3.3 SVR 温度预测模型参数寻优结果

当SVR 温度预测模型采用网格搜索与Kfold 交叉验证相结合的方法进行参数寻优时，网格的划分规则为a=[-10，10]、b=[-10，10]，网格搜索的步长均为0.5。通过比较发现，当K=4时，模拟结果的精度较高。为了清晰地呈现网格搜索结果，将（c，g）网格坐标转换为对数坐标（log2c，log2g）。 MSE 随log2c 与log2g 的变化情况如图5 所示。

实验结果表明，在4-fold 交叉验证下，SVR温度预测模型的最小均方误差为0.041 429，此时，c 的最优值为90.509 7，g 的最优值为0.5。

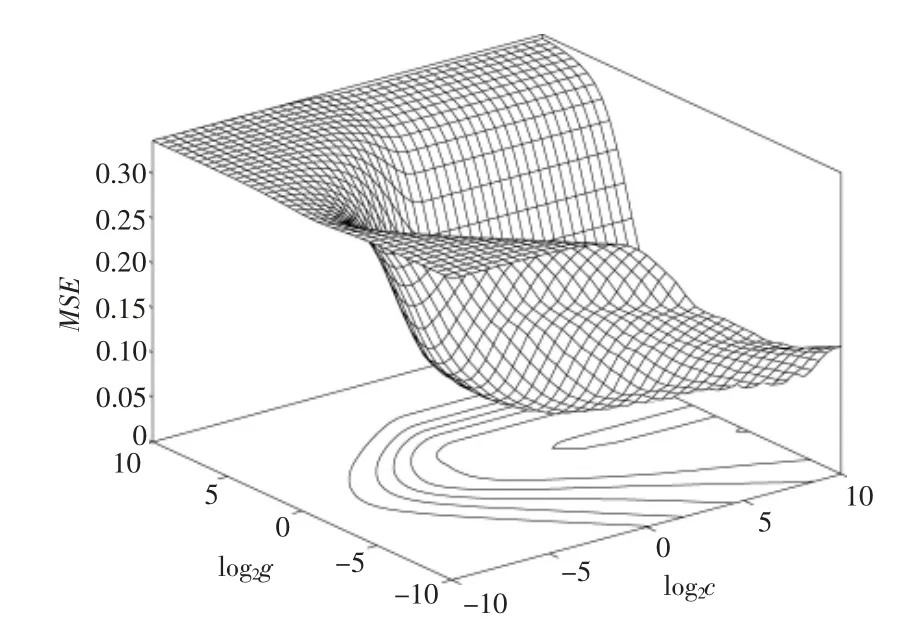
图5 参数选择3D 视图Fig.5 Parameter selection 3D map

3.4 最优参数下模型结果分析比较

本文分别构建原始数据未归一化处理、[-1，1]归一化处理和[0，1]归一化处理的SVR 温度预测模型，并且采用不同核函数进行验证。 PV/T组件温度预测实验对比结果如表1 所示。

由表1 可知，对于线性核函数和sigmoid 核函数，无论原始数据是否归一化处理，二者的相对误差均较大，平方相关系数均较小，整体预测精度均较低，说明线性核函数和sigmoid 核函数不适用于SVR 温度预测模型；对于多项式核函数和RBF 核函数，原始数据归一化处理后，二者的相对误差和均方误差均小于原始数据未经过归一化处理的情况，二者的相关系数均接近1，说明原始数据归一化处理后，PV/T 组件温度的真实值和预测值均具有较强的相关性。其中，多项式核函数对原始数据是否归一化处理更为敏感。当原始数据未经过归一化处理时，多项式核函数预测结果的相对误差和均方误差均较大，并且均达到了兆数量级，说明原始数据归一化处理对预测模型很有必要。在归一化处理过程中，综合比较了3 项预测评价指标发现，对本文实验数据进行[-1，1]归一化处理后，SVR 温度预测模型的预测精度高于[0，1]归一化处理后的情况。由表1 还可看出，在[-1，1]归一化处理的条件下，利用RBF 核函数的SVR 温度预测模型的相对误差和均方误差均较小，且相关系数均接近1，说明在SVR 温度预测模型中使用RBF 核函数时，预测精度最高。

表1 采用不同归一化方式、不同核函数时的预测结果Table 1 Prediction results when using different normalization methods and different kernel functions

BP 神经网络算法是各种预测模型的常用算法，通常具有较高的预测精度。本文构建了BP 神经网络温度预测模型，并与优化后的SVR 温度预测模型（以下简称为优化后的SVR 模型）进行实验对比，以衡量BP 神经网络温度预测模型的预测性能。这2 个模型均对原始数据进行[-1，1]归一化处理。图6 为优化后的SVR 模型的预测结果。

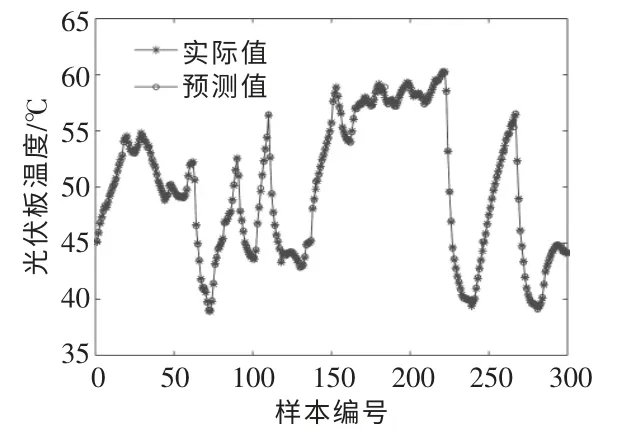
图6 优化后的SVR 模型的预测结果Fig.6 Prediction results of the optimized SVR model

图7 为BP 神经网络模型的预测结果。

图7 BP 神经网络模型的预测结果Fig.7 Prediction results of BP neural network model

由图6，7 可知，与BP 神经网络的预测结果相比，优化后的SVR 模型的模拟结果更接近实际测量结果。

图8 为优化后的SVR 模型的相对误差。图9为BP 神经网络模型的相对误差。

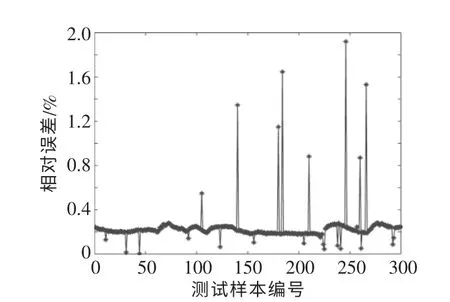
图8 优化后的SVR 模型的相对误差Fig.8 Relative error of SVR temperature prediction model after optimization

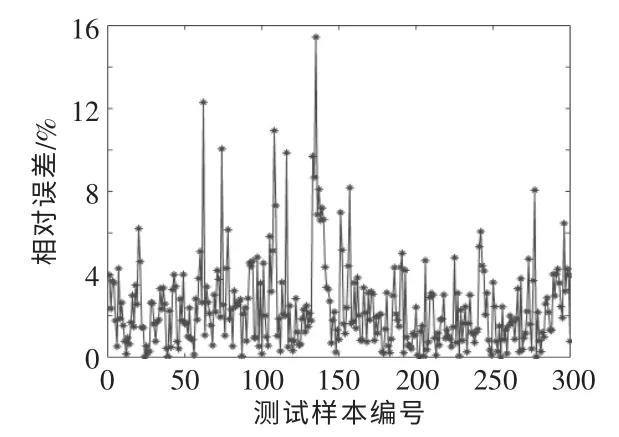
图9 BP 神经网络模型的相对误差Fig.9 BP neural network model prediction relative error

由图8 可知，优化后的SVR 模型预测结果的平均相对误差较小，预测结果的波动较小，预测结果均在预测精度允许范围之内。由图9 可知，BP神经网络预测结果的平均相对误差较大，尤其在水泵开启过程中，预测结果的波动较大，其中一部分预测结果超出了预测精度的范围。

表2 为优化后的SVR 模型和BP 神经网络模型的评价指标。

表2 两种模型的评价指标Table 2 Evaluation indicators of the two models

由表2 可知，优化后的SVR 模型的最大相对误差为1.92%，BP 神经网络模型的最大相对误差为15.44%。通过比较发现，BP 神经网络不适用于本文中的PV/T 组件温度的动态实时预测，这是由于BP 神经网络对于复杂的非线性系统具有一定的局限性，而且易陷入局部最优。本文的PV/T系统属于较为复杂的非线性系统，训练样本较少，因此，BP 神经网络模型的预测效果不佳。 SVR 是专门针对小样本提出的算法，在使用网格搜索寻优的情况下，可以在有限样本中得到全局的最优解。同时，SVR 还能够利用非线性变换将各环境变量，PV/T 组件进、出口温度以及冷却水流速等映射到高维特征空间，使得PV/T 组件温度预测模型具有较强的泛化能力。