DE-DA优化BP神经网络的知识掌握程度预测

唐立 李亚平 王利军

摘要：提出一种先用差分进化优化蜻蜓（Differential Evolution Dragonfly Algorithm，DE-DA）优化逆向传播（Back Propagation，BP）神经网络算法，使其运用在线上教学的知识掌握程度预测。DE-DA算法使得DA可选优继承，提高DA速度和精确度，再用DE-DA组合算法帮助BP神经网络找到全局优化权值和阀值，提高BP神经网络收敛效率，解决陷入局部极小值和收敛速度慢的问题。研究结果表明，DE-DA算法优化BP神经网络的权值和阈值，能有效提高网络训练的收敛速度和精确度，提高了整体预测效果。

关键词：BP神经网络;DA算法;DE算法

中图分类号：TP301.6;TP183  文献标志码：A  文章编号：1008-4657（2020）02-0012-06

0 引言

随着线上教学的广泛推广，人们越来越多的关注线上教学质量，学生线上学习情况等问题。线上教学过程中学生对所学的知识掌握程度的测评，能客观表现学生线上学习的情况，也是线上教学质量评估标准之一。

根据Kahraman[1-2]的方法，知识的掌握程度通过五个维度来衡量，即STG：学习当前章节知识的学习时长;SCG：对当前章节知识的重复学习次数;STR：储备知识的学习时长，即之前章节学习时长;LPR：储备知识的学习在线测试成绩;PEG：当前章节知识的考试成绩。以上这些数据具有较强的非线性和非稳定性，传统的模型因学习效率低或者陷入局部极小值而难以预测结果[3]。文献[4]通过遗传算法（Genetic Algorithm，GA）优化BP神经网络权值和阈值，有效地避免了陷入局部极小值，但是GA算法复杂的算法，使得寻优耗时过长。文献[5]用DA优化BP神经网络，提高了权值和阈值的寻优速度，但是在寻优过程中，易陷入局部最小值导致全局搜索能力较差。

DA算法具有良好的全局和局部寻优性能，但是该算法在择优过程中无法继承判断，而耽误了不少运算时间。DE算法是一种差分进化算法，是速度最快的进化算法，主要用于求解实数优化问题。针对这两种算法特点，本文提出一种DE-DA组合算法来优化BP神经网络，用DE算法对DA中的个体进行变异、交叉、选择操作，使DA择优继承，提高了DA寻优的速度，快速确定BP神经网络最优的权值和阈值，最終使得BP神经网络预测效果大幅提高。最后将其算法应用在线上教学的知识掌握程度预测上，通过实验，对比验证该算法的有效性和性能比。

1 DE-DA组合优化算法研究

1.1 DA算法

DA算法是Mirjalili等[6]提出的一种元启发式优化算法，它是模仿蜻蜓群体避敌、飞行和觅食等行为，同时对蜻蜓个体在全局和局部中寻找最优位置的算法[7]。DA算法具有较好的全局和局部搜索能力，可以帮助BP神经网络全局寻优。

通过表1可以看出，四种模型的精确度最低的是BP模型，GA-BP、DA-BP、DE-DA-BP模型对BP神经网络进行优化，提高了原来的BP模型的预测精度，从数据来看GA-BP模型与DE-DA-BP模型的预测精度较接近，但是DE-DA-BP模型的预测精度是最高的，这表明DE-DA组合优化BP神经网络算法适合于线上教学的知识掌握程度非线性特征预测，预测效果优良。

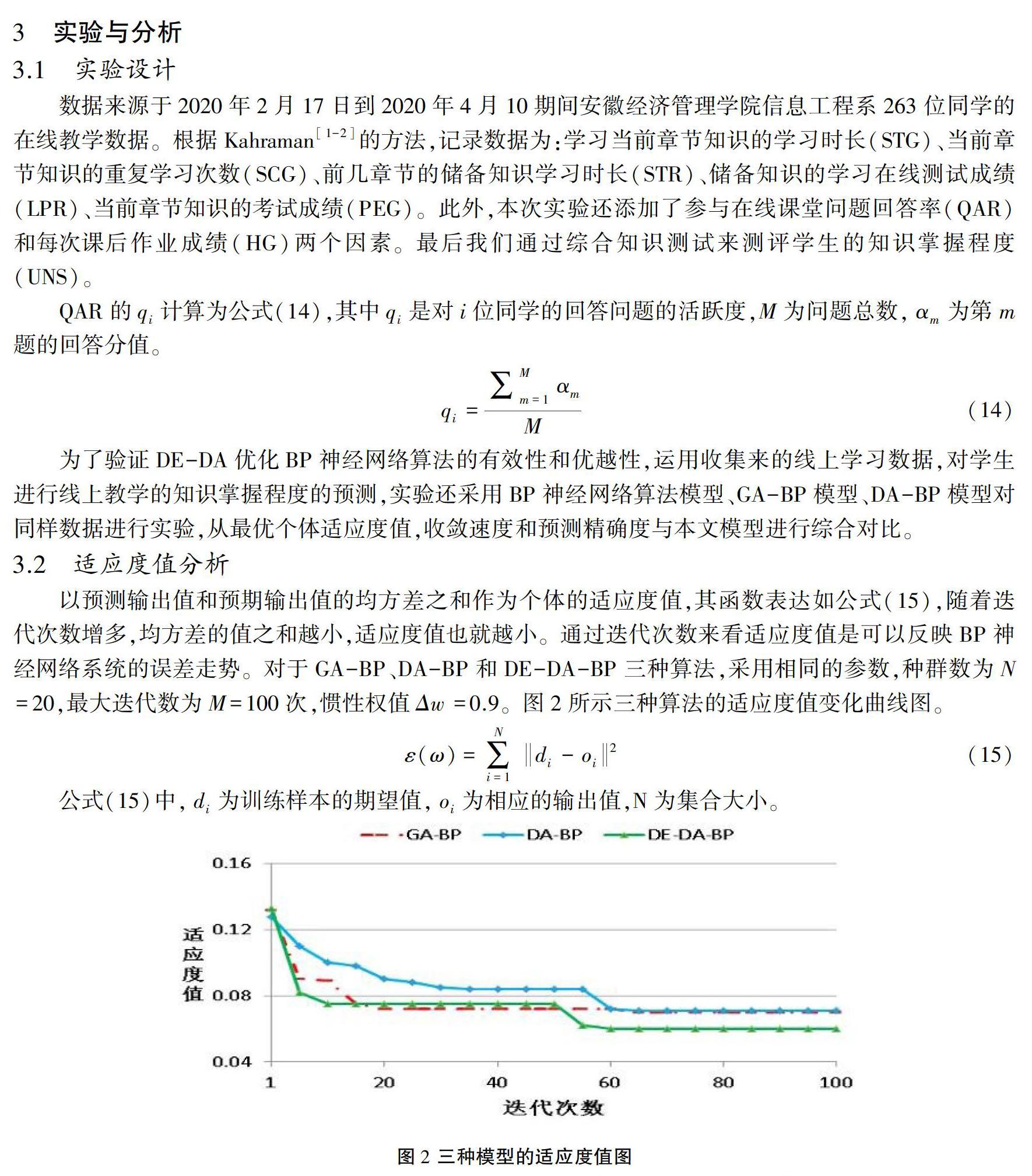
4 结论

本文针对线上教学知识掌握程度的非线性关系特性，提出运用DE-DA组合优化BP神经网络算法对知识掌握程度进行预测，结合DE和DA算法的优势，解决BP神经网络算法的极易陷入局部极小值和收敛速度慢的问题，在全局上对权值和阀值进行寻优，降低了BP神经网络的系统误差，提高精确度。把这种新算法运用知识掌握程度预测上，从实验结果和分析得出，DE-DA组合优化BP算法比BP、GA-BP和DA-BP算法精确度更高，收敛速度要快，能满足知识掌握程度的预测。

参考文献：

[1] Kahraman H T，Sagiroglu S，Colak I. Developing Intuitive Knowledge Classifier and Modeling of Users' Domain Dependent Data in Web[J]. Knowledge Based Systems，2013，37： 283-295.

[2] Kahraman H T，Designing and Application of Web-based Adaptive Intelligent Education System[D]. Turkey： Gazi University，2009：1-156.

[3] 范岩，马立平.优化BP神经网络的高校教学质量评价模型[J].统计与决策，2018，34（2）：80-82.

[4] 岳琪，温新.基于GA和BP神经网络的教学质量评价模型研究[J].内蒙古大学学报（自然科学版），2018，49（2）：204-211.

[5] 张霄，钱玉良，邱正，等.基于蜻蜓算法优化BP神经网络的燃气轮机故障诊断[J].热能动力工程，2019，34（3）：26-32.

[6] Mirjalili S. Dragonfly Algorithm：A New Meta-heuristic Opti-mization Technique for Solving Single-objective，Discrete，and Multi-objective Problems[J].Neural Computing & Appli-cations，2016，27（4）：1 053-1 073.

[7] 唐立，王利军.基于Spark的DA算法并行化研究[J].西昌学院学报（自然科学版），2019，33（4）：66-69.

[8] 赵齐辉，杜兆宏，刘升，等.差分进化的蜻蜓算法[J].微电子学与计算机，2018，35（7）：101-105.

[9] 黄文锋.基于改进神经网络的挖掘算法设计[J].现代电子技术，2018，41（14）：143-146.

[10] 唐立.基于PSO-Adaboost-BP的问题解决能力测评预测[J].韶关学院学报，2018，39（12）：18-22.

[责任编辑：郑笔耕]