考虑轨道伤损的列车-无砟轨道-桥梁系统动力特性

闫斌 谢浩然 潘文彬

摘要： 为探讨桥上无砟轨道损伤对列车-轨道-桥梁系统动力响应的影响规律，基于车辆-轨道-桥梁耦合动力学原理，基于ANSYS+SIMPACK联合仿真，建立了考虑墩台纵向支座刚度、轨道结构及层间接触特性的双线32 m简支箱梁桥CRTSⅢ型无砟轨道空间动力学模型。研究了时速200 km列车通过条件下，扣件伤损及轨道板和底座板间离缝对车桥系统动力响应的影响规律。研究表明：单个扣件失效对轨道动力响应影响有限，0.07 m板缝处轮轨竖向力骤变显著，钢轨竖向位移和钢轨节点反力增大明显;扣件连续失效对系统整体影响更大，其中相邻且对侧扣件失效影响最大;自密实混凝土沿轨道板横向完全脱空后，纵向离缝长度越大，对系统动力响应的影响也越大;相邻轨道板端部自密实混凝土都沿横向完全脱空对系统动力响应影响最大，轨道结构与桥梁结构的垂向加速度、竖向位移均增幅最大，增势最快;离缝长度1.2 m，轮重减载率接近限值，继续增加至1.6 m时，列车将脱轨;轨道板和桥梁的竖向振动随着离缝长度的增大显著增大，振动骤增会对轨道以及桥梁的耐久性产生不利影响，建议离缝长度检修限值可设为1.2 m，并应重点关注轨道板端部自密实混凝土界面脱空情况。

关键词： 轨道工程; 动力响应; 简支桥梁; 板边离缝; 扣件损伤

中图分类号： U213.2; U213.9+12  文献标志码： A  文章编号： 1004-4523（2020）04-0807-08

DOI：10.16385/j.cnki.issn.1004-4523.2020.04.019

引 言

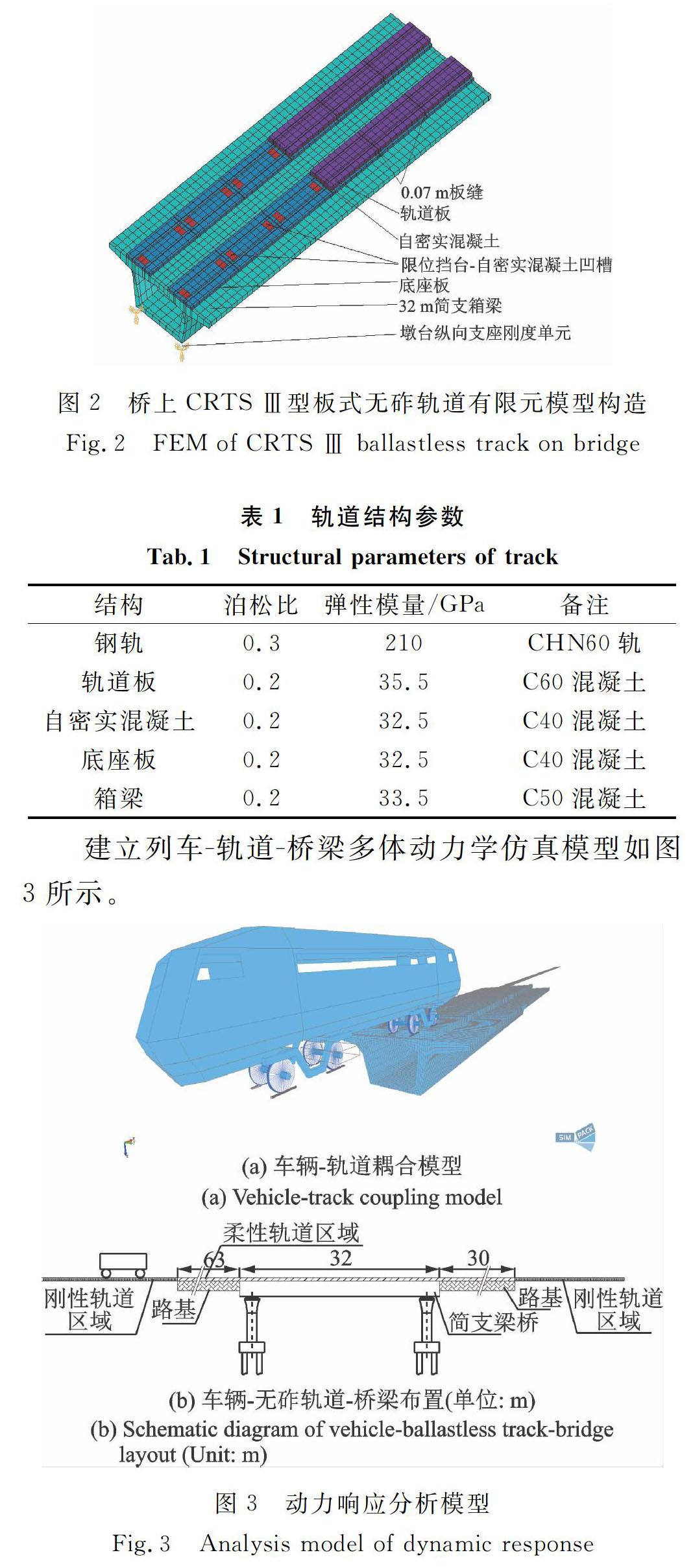
中国高速铁路网中，桥梁占比平均达50%以上，其中90%的桥梁为32 m双线无砟轨道简支梁[1]。为消除钢轨接头带来的轮轨动力冲击，减少后期养护工作量，通常采用无砟轨道无缝线路。如中国具有自主知识产权的桥上CRTSⅢ型单元板式无砟轨道，其采用分块式结构，底座板与自密实混凝土层间设置中间隔离层[2]，利用限位挡台传递轨道纵横向荷载。

国内外学者已针对列车作用下的无砟轨道的静动力学性能进行了较为广泛的研究，涉及土质路基[3-4]、简支梁[5]、钢混梁[6]等不同下部基础，并探讨了温度[7]、地震作用下[8]，砂浆离缝[9-10]、底板脱空[11]、温度翘曲变形[12]等损伤对无砟轨道静动力学性能的影响[13-14]。孙璐等[15]基于有限元理论建立了CRTSⅢ型板式无砟轨道结构，进行列车静荷载作用下结构静力特性分析，但未考虑列车动载荷对轨道动力特性的影响。宋小林等[10]利用ANSYS/LS-DYNA有限元软件建立了CRTSⅢ型无砟轨道动力有限元模型，分析了板边离缝对轨道结构冲击动力特性的影响规律，将列车模型简化为单轮对结构，动力响应中未充分考虑车辆自由度。鉴于CRTSⅢ型板式无砟轨道的特殊结构与传荷性能，对动荷载作用下桥上CRTSⅢ型无砟轨道系统动力性能及时域特征研究仍相對较少，扣件伤损与板下离缝条件对系统动力响应的影响规律仍不明确。

为研究无砟轨道损伤对列车作用下桥上CRTSⅢ型无砟轨道系统动力响应的影响规律，运用车辆-轨道-桥梁耦合动力学原理，以成灌线上某32 m简支箱梁桥为例，采用ANSYS+SIMPACK联合仿真，建立考虑下部结构刚度、限位挡台、无砟轨道及轨道层间接触特征的桥上CRTSⅢ型板式无砟轨道空间动力学模型[16]。在此基础上，进行模态响应分析，探讨轨道结构损伤对系统动力特性的影响，分析时速200 km列车作用下扣件伤损及轨道板下离缝组合工况对车-轨-桥系统动力性能的影响规律。

1 列车-轨道-桥梁多体动力学仿真模型

1.1 车-桥系统耦合振动模型  将钢轨视为Timoshenko梁，与下部轨道-桥梁系统视为单层弹性点支承接触以模拟真实情况，并用弹簧模拟WJ-8扣件三向刚度与阻尼约束，混凝土底座板结构通过参振质量的形式在桥梁动力学模型中予以考虑，自密实混凝土当作弹性垫层与周围结构通过一系列离散支承的线性弹簧相连，将轨道板和底座板看作双层弹性叠合梁[17]，如图1所示，在系统耦合动力分析中予以采用。

1.2 车辆动力学模型

基于中国CRH3型列车，建立了多体动力学车辆模型，由刚体+弹簧+阻尼器构成。主要组成有4个轮对、2个转向架、1个车体以及一、二系的悬挂系统， 车体和转向架均具有沉浮、横移、侧滚、点头、摇头5个自由度，轮对有沉浮、横移、侧滚、摇头4个自由度，即模型共有31个自由度。各元件采用力元（Force Element）连接，高速动车组参数参见文献[18]。

1.3 Ⅲ型轨道-桥梁有限元模型

按照固定+活动方式布置箱梁支座约束，考虑弹簧模拟墩台纵向刚度，建立了限位挡台与层间连续接触的CRTSⅢ型板式无砟轨道双线箱梁空间仿真模型（如图2所示），对底座、轨道板两端进行约束，节点耦合，各层之间采用Target170单元模拟3D刚性“目标”面，Contact174单元模拟3D柔性“接触”面，通过设置“接触对”模拟实际面-面接触。钢轨采用Beam188梁单元模拟，扣件系统采用Combin14线性弹簧单元模拟，轨道板、自密实混凝土层、底座板、箱梁均采用Solid45实体单元模拟，墩台采用Combin14弹簧单元等效模拟。轨道模型共6块预制单元轨道板，采用5.6 m和4.925 m两种规格，按4.925 m×2+5.6 m×4拼装组合，相邻单元板轨缝为0.07 m，模型总长32.6 m。根据中国《高速铁路设计规范》[16]，双线简支梁桥墩台纵向刚度取35000 kN/m，扣件系统采用WJ-8型扣件，垂向阻尼取为4×104 N·s/m，纵向刚度按照15000 N/0.63 m设置，横向刚度为5×107 N/m，垂向刚度为3.5×107 N/m，布置间距为0.63 m。相关参数设置如表1所示。

2 耦合动力学模型验证

高速铁路列车以250 km/h速度通过简支箱梁上板式无砟轨道，将动力学分析结果分别与原铁道部科技司授权软件TTBSIM计算结果和沙河特大桥系统的现场试验结果进行比对[19]。设置列车行驶速度为250 km/h，积分时间为3 s，积分步长取0.001 s进行离线计算。

计算分析得到车辆、桥梁动力学结果如表2所示，其中列车和被测桥梁动力响应均为计算和实测的最大值。

从表2的比对结果可以看出，受限于简化的数学模型、数值分析方法和实际环境的随机性，跨中竖向动挠度和加速度峰值存在一定差异，总体上，本文计算结果与TTBSIM软件以及沙河特大桥实测值分布规律基本吻合，证明本文联合仿真中实体三维耦合模型是正确的。

3 扣件失效对车-轨-桥系统动力性能影响  针对轨道系统中可能出现的扣件局部失效情况（将失效扣件的竖向刚度和阻尼均取为0），设置多个工况，研究单个扣件失效、对侧扣件失效、相邻且对侧扣件失效、间隔且对侧扣件失效等工况下， 200 km时速列车作用下系统各结构受力以及加速度等动力响应。

3.1 单个扣件失效

图4为单个扣件失效（工况1）的情况下系统动力响应对比。可以看出，工况1中，轮轨竖向力极值几乎没有变化，且均在轨缝处出现激增，增幅约6.3%;另外，车体垂向加速度和构架垂向加速度变化也不明显;失效扣件处钢轨节点反力增大明显，由19.4 kN增至34.5 kN，增幅为77.8%;钢轨垂向加速度幅度的增大最明显，从141 m/s2增大至275 m/s2，增幅为95%;针对轨道板与桥梁结构，其垂向动加速度变化不明显。由此，工况1中单个扣件失效对于列车系统动力响应影响有限，列车行驶平稳性和安全性依然能得到保证;对轨道结构动力特性影响较大，钢轨节点反力显著增大;对下部桥梁动力响应影响有限。

3.2 扣件失效组合

基于现实环境，在列车-轨道-桥梁动力耦合系统中，还有可能出现多个扣件失效的伤损情况，即工况2、工况3和工况4中所列举的扣件状态（如图5所示）。

分析表3可以看出，轨道结构中钢轨竖向位移在各组扣件失效的工况中都会变大，其中工况1，2和4均比正常情况下增大了51%左右，而工况3相比正常情况增幅128%，达到了3.3 mm，这时已经超过2 mm规定限值;工况3中轨下扣件失效处，钢轨结构垂向加速度增大了近乎2.3倍，达到46.8g，相邻钢轨节点的反力也从19.4 kN增至48.7 kN，增幅1.5倍，对比之下，工况1，2，4中各系统响应相对增加较小;另外，车体、转向架和轨道板结构在失效扣件处的垂向加速度只有小幅波动，几乎不变。此外，桥梁的竖向位移和垂向加速度在扣件没有连续失效情况下变化不明显，而在工况3时，桥梁竖向位移从0.24 mm增至0.42 mm，增幅为75%。桥梁垂向加速度从0.42 m/s2增大到0.52 m/s2，可見钢轨扣件失效虽然对于列车行驶的平稳性、舒适性影响较小，但是却增大了钢轨、轨道板和桥梁结构的竖向位移，长此以往对车桥系统带来的累计损伤不容忽视。

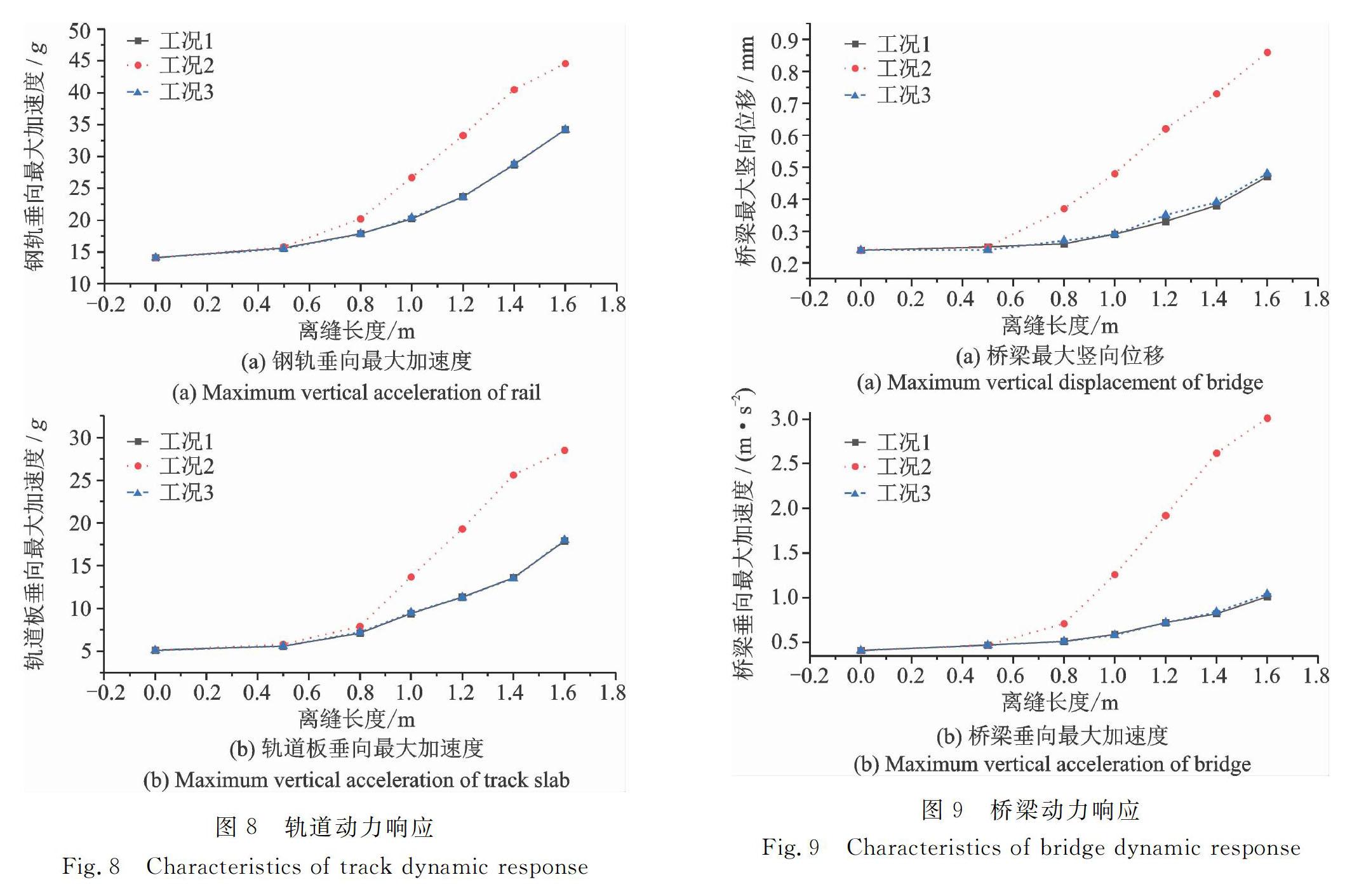
4 板下离缝组合对车-轨-桥系统动力性能影响  在自密实混凝土未全部贯通轨道板情况下，对行车影响而言并不是最不利情况[20]。因此，本文考虑板下充填层横向2.5 m范围、竖向0.09 m范围内全部脱空，充分考虑在离缝位置组合下离缝长度对耦合系统动力学特性影响。如图6所示，行车速度200 km/h下，设置三种工况，离缝纵向长度分别取0.5，0.8，1.0，1.2，1.4，1.6 m，进行对比性研究。

4.1 车辆动力特性

图7为三种离缝工况下，部分车辆系统动力性能对比。由图7（a）可以看出，在离缝长度不超过0.5 m情况下，各工况下车体垂向加速度变化均不明显;当离缝长度超过0.5 m时，随着离缝长度增大，车体垂向加速度变化幅度也随之增加，其中工况1相对于工况2，3增幅较小，从0.093 m/s2增大到0.101 m/s2。工况2和工况3增长趋势基本一致，且当离缝长度达到1.6m时，车体垂向加速度最大值分别为0.147和0.146 m/s2。因此，所有工况下车体垂向加速度均满足1.3 m/s2限值要求;图7（b）和（c）中，在离缝长度不超过0.5 m时，各组工况下轮轨竖向力极值变化均不甚明显;当超过0.5 m时，轮轨竖向力最大值呈增大趋势，而轮轨竖向力最小值则呈递减趋势。其中工况2下极值变化幅度最大，离缝长度1.6 m时，最大值由84.1 kN增大到了106.4 kN，增幅26.5%，最小值由64.1 kN减小到了0，表明已经脱轨。

4.2 轨道动力特性

表4给出了离缝组合下，轨道系统动力性能积分计算结果。

由图8可以看到，各工况下钢轨、轨道板的垂向加速度随离缝长度的增大而增大。这其中工况2中增幅最大，钢轨垂向加速度从14.1g增至44.6g，轨道板垂向加速度从5.1g增至28.5g，离缝导致的结构竖向振动越大，对轨道整体动力响应性能的影响也越大。

4.3 桥梁动力特性

提取箱梁振动数据，图9反映了离缝组合下桥梁力学性能。

图9（a）中可以看到，随离缝长度增大，三种工况下桥梁竖向位移均呈增大的趋势，但都远小于列车活载下竖向挠度限值40 mm[19];在图9（b）中，桥梁垂向加速度变化趋势与桥梁竖向位移类似，都在工况2中增幅最大，增势最快，从0.41 m/s2增大到3.01 m/s2，满足3.5 m/s2限值。结合图7，在离缝长度达到1.2 m后，轮重减载率已经接近限值。离缝长度达到1.4 m后系统动力响应剧烈，离缝长度达到1.6 m时，列车已经脱轨，建议控制离缝长度不超过1.2 m。

5 结 论

本文基于有限元软件ANSYS与动力学分析软件SIMPACK，建立了考虑墩台纵向支座刚度、轨道结构特点及层间接触特性的双线简支箱梁桥上CRTSⅢ型板式无砟轨道空间耦合模型。研究了200 km/h列车过桥速度下扣件失效、离缝组合工况下系统的位移与力学性能。得到的主要结论包括：

（1） 单个扣件失效对于列车动力响应性能影响有限，列车行驶安全平稳性依然能够得到保证;对桥梁动力响应影响较小;对轨道结构动力特性影响较大，其中失效扣件位置钢轨竖向位移和节点反力增大明显，会影响轨道结构的安全性与耐久性。

相较与单个扣件失效工况，扣件连续失效对于系统影响更大，其中相邻且对侧扣件失效工况下影响最大，在检修工作时应予以关注。

（2） 离缝组合工况下，自密实混凝土沿轨道板端部横向完全脱空后，纵向离缝长度越大，对系统动力响应性能的影响也越大。以轨道板一端自密实混凝土脱空工况为例，离缝长度不超过1.0 m，影响较小;当离缝长度超过1.0 m时，特别是当离缝长度达到1.6 m，轮重减载率已接近限值，影响列车行驶的安全性。与脱空长度1.0 m相较，轨道板垂向加速度增幅很大，达到90.1%，对轨道结构耐久性产生影响。

相邻轨道板端自密实混凝土都沿横向完全脱空工况对系统动力响应的影响是最大的。其中，纵向离缝长度达到0.5 m时，车-桥系统各动力响应参数显著增大，接近1.2 m时列车轮重减载率急剧接近限值。

轨道板和桥梁结构的竖向振动随着离缝长度的增加也明显增大，虽然在限值范围以内，但是竖向振动骤增会对轨道以及桥梁服役耐久性产生不利影响，建议离缝长度检修限值可设为1.2 m，重点关注相邻轨道板端部板缝处自密实混凝土脱空情况。

参考文献：

[1] Yan Bin， Dai Gonglian， Hu Nan. Recent development of design and construction of short span high-speed railway bridges in China[J]. Engineering Structures， 2015，100： 707-717.

[2] 王繼军，王 梦，刘伟斌，等.CRTSⅢ型板式无砟轨道系统技术[J].中国铁路，2017，（08）：11-15.

WANG Jijun， WANG Meng， LIU Weibin， et al. Technology of CRTSⅢ ballastless track system[J].Chinese Railways， 2017，（08）：11-15.

[3] 徐庆元，李 斌，范 浩.路基不均匀沉降对列车-路基上无砟轨道耦合系统动力特性的影响[J].铁道科学与工程学报，2012，9（03）：13-19.

XU Qingyuan， LI Bin， FAN Hao. Influence of uneven settlement of subgrade on dynamic characteristic of train-ballastless track on subgrade coupling system[J]. Journal of Railway Science and Engineering， 2012，9（03）：13-19.

[4] Auersch L， Said S. Track-soil dynamics——Calculation and measurement of damaged and repaired slab tracks[J]. Transportation Geotechnics， 2017， 12： 1-14.

[5] Podworna Monika. Dynamic response of steel-concrete composite bridges loaded by high-speed train[J].Structural Engineering and Mechanics，2017，62（2）：179-196.

[6] 李培刚，刘学毅，黎国清.CA砂浆脱空对桥上单元板式轨道动力特性的影响研究[J].中国铁道科学，2014，35（03）：20-27.

LI Peigang， LIU Xueyi， LI Guoqing. Influence of CA mortar void on dynamic characteristics of unit slab track on bridge[J]. China Railway Science，2014，35（03）：20-27.

[7] 闫 斌， 刘 施， 戴公连， 等. 中国典型地区无砟轨道非线性温度梯度及温度荷载模式[J]. 铁道学报， 2016， 38（8）： 81-86.

Yan Bin， Liu Shi， Dai Gonglian， et al. Vertical temperature nonlinear distribution and temperature mode of unballasted track in typical areas of China[J]. Journal of the China Railway Society， 2016， 38（8）： 81-86.

[8] YAN Bin， LIU Shi， PU Hao， et al. Elastic-plastic seismic response of CRTS II slab ballastless track system on high-speed railway bridges[J]. SCIENCE CHINA Technological Sciences， 2017， 60（6）： 865-871.

[9] Han J， Zhao G， Xiao X， et al. Effect of cement asphalt mortar damage location on dynamic behavior of high-speed track[J]. Advances in Mechanical Engineering， 2018， 10（4）： 1687814018770779.

[10] 宋小林，吕天航，裴承杰.板边离缝对CRTSⅢ型轨道-路基动力特性的影响[J].西南交通大学学报，2018，53（5）：913-920.

SONG Xiaolin， L Tianhang， PEI Chengjie. Influence of interface crack on impact dynamic properties of CRTS Ⅲ slab track-subgrade system[J]. Journal of Southwest Jiaotong University，2018，53（5）：913-920.

[11] 任娟娟，严晓波，徐光辉，等.底座板脱空对板式无砟轨道行车动力特性的影响[J].西南交通大学学报，2014，49（06）：961-966.

REN Juanjuan， YAN Xiaobo， XU Guanghui， et al. Effects of contact loss underneath concrete roadbed on dynamic performances of slab track-subgrade system[J]. Journal of Southwest Jiaotong University，2014，49（06）：961-966.

[12] 張重王，苏成光，刘学毅， 等.温度梯度与板下脱空对列车轨道系统动力响应的影响[J].铁道学报，2017，39（4）：85-93.

TRUONG Trong Vuong， SU Chengguang， LIU Xueyi， et al. Influence of temperature gradient and void beneath slab on dynamic response of high speed track system[J]. Journal of the China Railway Society，2017，39（4）：85-93.

[13] 戴公连，王 蒙，刘文硕.动载下CRTSⅡ型无砟轨道-简支梁桥变形试验研究[J].振动与冲击，2018，37（07）：102-108.

DAI Gonglian， WANG Meng， LIU Wenshuo. Tests for deformation of a simply supported beam bridge with CRTS Ⅱ ballastless track subjected to dynamic loads[J]. Journal of Vibration and Shock，2018，37（07）：102-108.

[14] 戴公连，刘翔宇，刘文硕.简支梁上CRTSⅡ型无砟轨道动力特性的试验研究[J].华南理工大学学报（自然科学版），2017，45（04）：95-102.

DAI Gonglian， LIU Xiangyu， LIU Wenshuo. Experimental research on dynamic properties of CRTSⅡ ballastless track on simply-supported beam[J]. Journal of South China University of Technology（Natural Science Edition） ，2017，45（04）：95-102.

[15] 孙 璐，段雨芬，杨 薪.高速铁路 CRTS Ⅲ型板式无砟轨道结构受力特性研究[J].铁道工程学报，2013，（11）：32-39.

SUN Lu， DUAN Yufen， YANG Xin. Static response analysis of CRTS Ⅲ ballastless track structure[J]. Journal of Railway Engineering Society，2013，（11）：32-39.

[16] 国家铁路局.TB 10621-2014，高速铁路设计规范[S].北京：中国铁道出版社，2014.

National Railway Administration of the Peoples Republic of China. TB 10621-2014， Code for design of high speed railway[S]. Beijing：China Railway Publishing House Co.， Ltd.， 2014.

[17] 徐 磊，翟婉明.车辆-轨道系统时-空随机分析模型[J].铁道学报，2018，40（01）：74-79.

XU Lei， ZHAI Wanming. Stochastic model used for temporal-spatial analysis of vehicle-track coupled systems[J]. Journal of the China Railway Society，2018，40（01）：74-79.

[18] 罗 震.高速铁路无砟轨道结构受力及轮轨动力作用分析[D].成都：西南交通大学，2008.

LUO Zhen. Analysis of structure mechanics and wheel/rail dynamic interaction of ballastless track in high-speed railway[D]. Chengdu： Southwest Jiaotong University， 2008.

[19] 翟婉明， 夏 禾. 列车-轨道-桥梁动力相互作用理论与工程应用[M]. 北京： 科学出版社， 2011.

ZHAI Wanming， XIA He. Train-Track-Bridge Dynamic Interaction： Theory and Engineering Application[M]. Beijing： Science Press，2011.

[20] Truongtrong Vuong. CRTSⅠ型板式軌道的动力特性及伤损影响研究[D].成都：西南交通大学， 2015.

Truongtrong Vuong. Study on dynamic characteristics and disease analysis of CRTS I prefabricated slab track[D]. Chengdu： Southwest Jiaotong University， 2015.

Abstract： In order to investigate the impact of the track damages on the dynamic response of train-track-bridge system， based on the principle of train-track-bridge coupling dynamics and ANSYS+SIMPACK co-simulation， the spatial dynamics model of CRTS Ⅲ ballastless track with 32 m simply supported bridge considering the longitudinal stiffness of supports， the track structure and interlayer contact characteristics are established. The influence of fastener damage and the crack between the track slab and the baseplate on the dynamic response of train-bridge system under 200 km/h running train is studied. The results show that the failure of a single fastener has a limited impact on the dynamic response of the system. The vertical force of the wheel-rail at the 0.07 m slab gap increases significantly， and the vertical displacement of the rail and the inverse force of the rail joint increase obviously. The continuous failure of the fasteners has a greater impact on the system while the adjacent and opposite side fasteners have the greatest impact. After the self-compacting， concrete is completely cracked， the greater the longitudinal length of crack， the greater the influence on the dynamic response. The complete cracked of the self-compacting concrete at the end of the adjacent track slab has the greatest influence on the dynamic response， and the vertical acceleration and displacement of the track-bridge structure increase quickly. When the length of the interface crack is 1.2 m， the wheel weight reduction rate is close to the limit value. If the interface crack length increases to 1.6 m， the train will be derailed. The vertical vibration of the track slab and the bridge increases significantly with the increase of the crack length. The vibration surge will adversely affect the durability of the track and bridge structure. It is suggested that the limit value of the interface crack length can be defined to 1.2 m， and attention should be paid to the interface crack of self-compacting concrete at the edge of the track slab.

Key words：track engineering; dynamic response; simply-supported bridge; interface crack; fastener damage