数学知识点“源”与“流”的实践探究
2020-08-13吴志凯
吴志凯


新冠肺炎疫情防控期间,为了保障全市30多万小学生的优质线上教育,中山市教育局相继推出在线教学方案,组织全市100多位市级骨干教师上演一场不同寻常的“战役”。其中小学数学的在线教育以线下、线上组成的形式进行。线下教学指教师设计好前置性探究学习单让学生课前探究新知;线上教学指教师根据前置性探究学习单的设计问题和学生自主探究的情况开展视频教学。笔者有幸参加了这次在线教学的设计,发现学生的前置性探究学习单的设计关键,是让学生潜移默化地感受到每个知识点“源”与“流”,感受知识点“源”与“流”带来的研究乐趣和智慧生长。
本文所提的“源”是指知识点的来源,知识的起点;“流”是指知识点的延伸和发展,或学生的后续学习。中山市教研员刘燕主编的《中山市小学数学教学要义》一书中曾详细地梳理了各单元的前期学习和后续学习,与本文中提到的“源”与“流”有着相同的意思。那么,如何让学生感受知识的“源”与“流”,让学生在探究中智慧生长?本文以“数与代数”中《在直线上表示负数》和“图形与几何”中《圆柱的认识》两节课的设计为例,阐述如何让学生了解知识点“源”与“流”及其重要性。
一、找准知识的“源”与“流”,有利于知识的承前启后
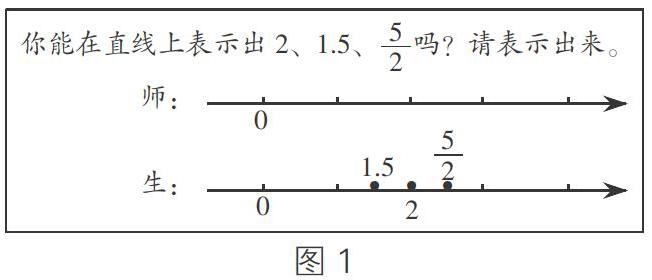
《义务教育数学课程标准(2011年版)》指出,教师教学应该以学生的认知发展水平和已有的经验为基础,注重启发式,在教学中,要注重知识的“生长点”与“延伸点”。以六年级下册《在直线上表示负数》为例,课本中以“四个小朋友所走的方向不同,距离不同”为情境,引出如何在一条直线上表示他们的距离和方向。显然,教材的设计是通过直观的情境抽象出直线,引发学生的思考,实现了直观到抽象的过程,这只是教材的表象。设计中,教师往往忽视了学生已有的经验、知识的关键点,缺乏唤醒学生对新知与旧知的联系,知识的零散导致学生认知的困难。我们应该努力挖掘教学内容的“生长点”和“延伸点”,找准知识点的“源”与“流”,给学生的理解扫除障碍。我们对知识点的“源”与“流”找得越准,找得细,学生对知识的理解就会越清晰越容易。如这节课,通过查阅资料,我们可以发现,早在二年级学习《万以内数的认识》时,学生已经初步接触在直线上表示整数,到了三年级学习了《分数的初步认识》《小数的初步认识》,学生又进一步学习了用直线表示分数和小数,四五年级时,学生学习了《大数的认识》《小数的意义和性质》《分数的意义和性质》之后,经常运用直线表示数。可见,学生对用直线表示数并不陌生,并且有很丰富的经验,而本节课就是建立在学生已经很熟悉用直线表示整数、分数和小数的基础上进一步表示负数。因此,这节课的关键点就应该以在直线上表示整数、分数和小数为铺垫,引出负数的表示方法,然后,再借助有负数的数轴,进一步认识相反意义的量、一一对应的关系等,达到承前启后的效果。下面是设计的片段图:
通过收集学生前置性探究学习单发现,学生对在直线上表示整数小数和分数的经验丰富,都能够正确地表示出来。这时,教师再顺势出示情境,从情境中抽象出下面的问题:
师:看来同学们对以前的知识掌握得很棒!那么-1,-2又应该在上面的直线哪个位置表示呢?
学生有了之前旧知的回顾,唤醒了在直线上表示数的经验,通过调查分析,学生通过独立思考,都能想到延长“0”左边的线,表示出-1,-2。
这说明,找准相关联知识点,除了能够帮助学生建立表象,克服解决问题的困难,还能使学生知识的认知有序地链接,起到承前启后的作用。
二、看准知识的“源”与“流”,引导学生类化研究方法
教育应注重教学方法和策略,正如数学家乔治·波利亚所说:“完善的思想方法犹如北极星,许多人通过它而找到正确的道路。”秉承这一教育理念,教师在教学中应看准知识的“源”与“流”,引导学生掌握研究方法。特别是线上教学,前置性探究学习单的设计更应该让学生明确一类问题的研究方法,使学生在自主探究中少走弯路。如《圆柱的认识》这节课是属于“图形与几何”的范畴,在此课之前,学生已经对平面图形(长方形、正方形、三角形、梯形等)和立体图形(长方体、正方体)有过系统的学习,教材也明显指出:我们学过的正方体和长方体都是由平面围成的立体图形,现在再来研究一种立体图形——圆柱。可见,圆柱的认识和学过的平面图形、立体图形是一系列的,它们的研究方法应该有着大同小异之处,都是通过观察图形的构成,了解图形各边的数量关系,探究点、边、面的内在联系等,找到它们的图形的共性。但是,学生由于认知的经验偏少,对运用知识迁移的方法相对薄弱,不容易准确找到研究问题的方法。因此,这需要教师梳理图形研究方法的共性,对研究的内容进行归类与引导,激发学生研究的潜能。对于这节课的前置性探究学习单,我们可以如图3那样设计。
通过唤醒学生的回忆,了解之前图形特征的研究方法,启发学生思考:圆柱的认识也是属于图形的认识,可以运用以前的方法研究圆柱的特征(如图4)。
數学课程标准指出,分类是一种重要的数学思想。在研究数学问题中,往往需要通过分类讨论解决问题,分类的过程就是对事物共性的抽象过程。这样的设计,不但结合了数学这门学科的特点,也符合小学生的认知规律。它不仅体现了数学结果的形成过程,也体现了数学思想的形成过程,培养了学生用数学的眼光认识和处理同类事物或数学问题的能力,符合新时代培养学生数学核心素养所追求的目标。
三、把准知识的“源”与“流”,帮助学生建构知识体系
建构主义认为,学生切实掌握知识的表现,就是让学生把知识形成结构性的认识,懂得对知识进行迁移和运用。因此,在教学设计中,要注意知识点之间的内在联系和逻辑关系,教师还要帮助学生将零散的知识点整理、排序,使知识系统化、条理化、网络化,使学生构建比较完整的知识体系,从而实现对知识的理解从点到面、从面到链式的转变。如在六年级下册《圆柱的认识》中,对圆柱“高”的概念的教学,大部分教师都是让学生自行画高,然后直接出示课本中“高”的概念。表面上看,学生似乎已经掌握了“高”的概念,但如果进一步提问学生:为什么你认为所画的线段就是圆柱的“高”时,很多学生答不出其所然。显然,学生并没有真正理解圆柱的“高”。如何让学生真正理解“高”的概念,为什么自己所画的线段就是“高”?由于概念的抽象,教师需要引导学生把知识放在一个知识体系里面研究,找出“高”的概念、形成过程以及和原来所学的哪些知识有联系,自然就可以解决这个问题了。比如图5中,为什么说两个底面中心点之间的连线就是圆柱的“高”?我们不妨在这两个底面的中心点,过点做两条平行线。这时可以发现,原来现在所学的“高”,就是原来两条平行线之间的距离。我们还可以发现,两条平行线之间的距离处处相等,从而又可以证明圆柱有无数条高且相等。因此设计时,我们不妨把知识放在一个体系里面,抓住知识之间的前后联系,把知识尽可能连接起来,学生学起来就变得轻松,问题就会迎刃而解。
除此之外,每一节前置性探究学习单的设计,都应该在课前的设计和课后的归纳引导学生梳理知识点,把每堂课教学的知识置于整体知识的体系中。以六年级下册《在直线上表示负数》为例,当学生学习完新知后,要让学生了解这个知识点的知识结构和研究的框架(图6),逐步养成构建知识体系的良好习惯。数学课程标准指出,注重知识的结构和体系,处理好局部知识与整体知识的关系,有利于帮助学生厘清知识之间的区别和联系。
总之,要设计好前置性探究学习单,教师应当找准、看准、把准数学知识点的“源”与“流”,通过示范和归纳,使学生了解知识的前后联系,养成建立知识体系的习惯,感悟数学的基本思想,从而提高学习的针对性和有效性。
责任编辑 罗 峰
