基于STM32的板球控制系统的优化设计与研究

张鹤严 邵天洋

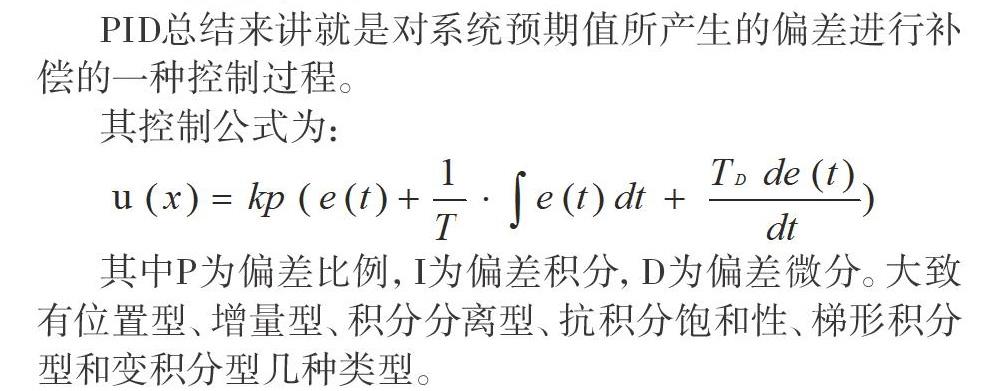
摘   要：板球系统是一个比较复杂的，具有非线性的不稳定系统，它既可以作为实验模型也具有其复杂性并与诸多控制类系统具有共通性，所以实现其稳定性的控制，是一项重要的课题。本文以平板上运动的小球作为被控对象，摄像头将采集到小球的位置图像，反馈给STM32系列单片机，来控制动作电机以对小球进行轨迹规划、定位控制等，从而探寻和验证机器人稳定移动的方法。从简单的电机稳定控制，到变积分PID调节，实现了电机的速度内环和位置外环的双闭环控制，最后对图像数据进行了优化处理。建立了一个控制机器人平衡的模型，给机器人研究工作者提供了新的平衡控制和优化数据的方法。

关键词：PID调节  板球控制系统  图传数据优化  STM32系列单片机

中图分类号：TP273+.4                            文献标识码：A                        文章编号：1674-098X（2020）06（a）-0152-03

Abstract： The cricket system is a complex， nonlinear and unstable system. It can be used as an experimental model， but also has its complexity and is in common with many control systems. Therefore， it is an important task to control its stability. In this project， a small ball moving on the plate is taken as the controlled object. By collecting the position image of the ball from the camera and feeding it back to the STM32 series SCM， the motor is controlled to conduct trajectory planning and positioning control for the ball， so as to explore and verify the method of stable movement of the robot. From the simple motor stability control to the variable integral PID regulation， the motor speed inner loop and the position of the outer loop of the double closed-loop control， finally the image data optimization processing. A balance control model is established， which provides a new method of balance control and data optimization for robot researchers.

Key Words： PID regulation; Cricket control system; Optimization of graph transmission data; STM32 series SCM

目前，机器人被广泛应用于汽车、飞机、轮船、手机、家电、等方面。在操作方面，机器人从根本上讲是处于不稳定状态的，很难将其进行稳定控制，所以在实际应用中存在诸多的问题，而控制系统的稳定性则是其中一个至关重要的话题。

现如今板球控制系统的滤波和PID算法两方面相关的技术已经接近成熟，很再难有所突破，但板球控制系统的处理速度和稳定性的确还有待优化和提升，所以我们决定在前人的基础上寻求突破，通过在摄像头图像处理和传回的帧数组上进行创新，以小范围预期扫描、缩小成像规模，来优化程序复杂而引起的处理速度缓慢、反应迟钝等问题，从提高运作效率方面切入作为突破的契机。

1  系统方案

本系统主要由机械模块、芯片控制模块、摄像头图传模块、动作模块、电源模块组成，下面分别论证这几个模塊的选择。

1.1 处理芯片的论证与选择

方案一：STC51系列单片机是在现应用较为广泛的单片机中价格较为低廉的一种：其内部集成专用复位电路，2路PWM，针对电机控制，强干扰场合，但是此芯片的晶振频率较低，而且性能很差，当传输数据量较大时速度难以满足运算要求，并且无法承担复杂的运算以及图像显示。该系列其功能单一，片内资源匮乏，且需要仿真器来实现软硬件调试，较为烦琐。

方案二：STM32F103系列单片机是在STM32系列单片机中价格最低的芯片，此芯片为ARM 32位的Cortex-M3，具有最高72MHz工作频率，可进行单周期乘法和硬件除法，较STC51系列单片机相比性能优越，且IO口及片内硬件资源丰富，可轻松进行大量的运算。但对于摄像头等高速器件处理能力仍然较差，如果加入一些复杂的算法后如：霍夫曼圆算法等，处理器的处理速度会达不到预期效果而出现传回图像卡成PPT的现象，难以应付大量的复杂运算。

方案三：STM32F429系列单片机是在STM32系列单片机中价格较高的芯片，此系列芯片较F1系列芯片相比，内核为Cortex-M4，具有最高180MHz工作频率，并且主频带DSP，不少的集成外设被加强，而且存储器的Flash和SRAM加大了很多，相对来讲此类芯片性价比更高。

综上所述本系统芯片选择为方案三。

1.2 机械结构与硬件选择

1.2.1 机械结构

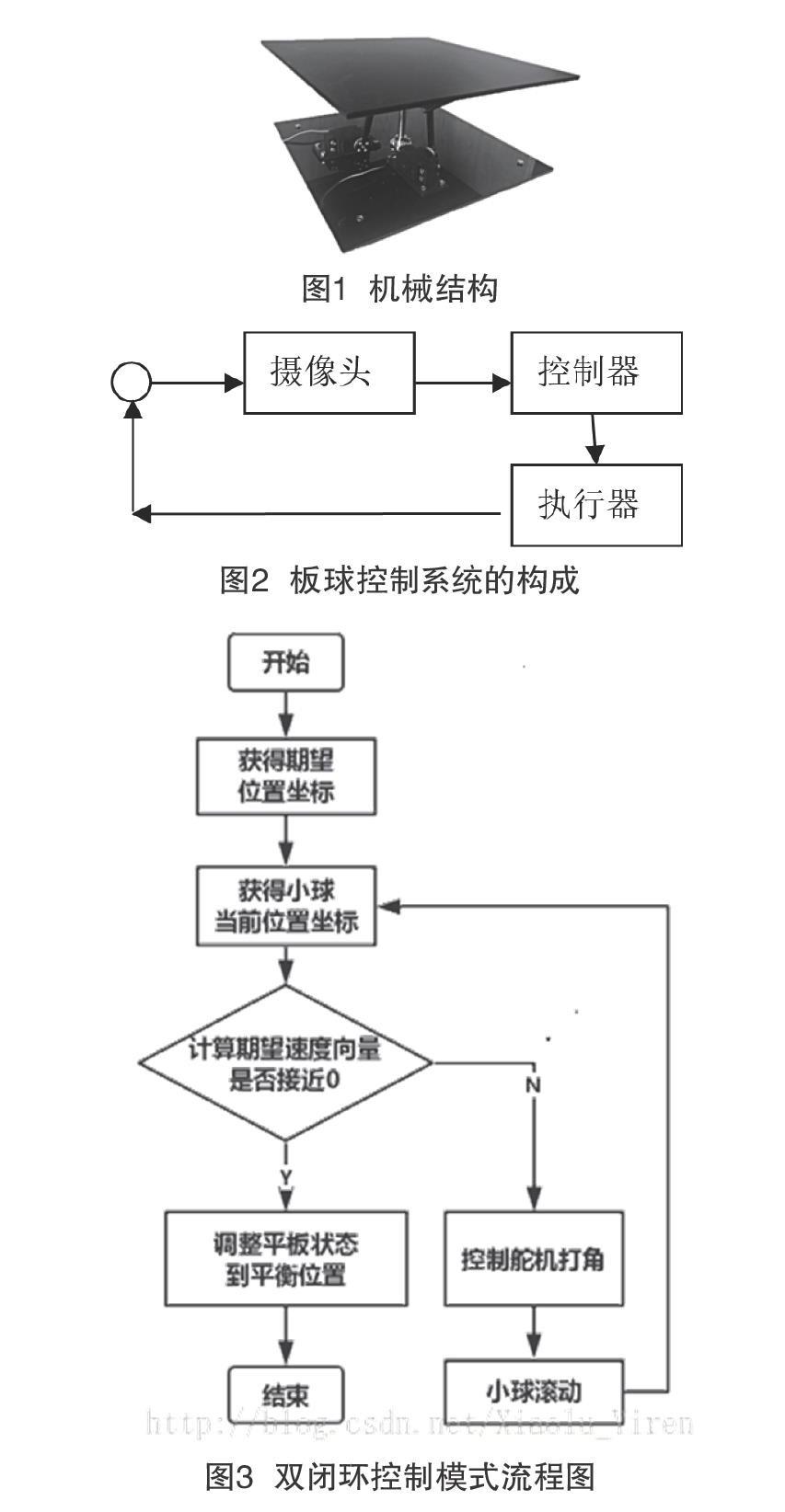
板球控制系统的机械结构具有2个自由度，平板中心为支撑点下方与底板上的支撑杆相连，在相邻两侧中心点的下方分别与底板上的动作电机机臂相连，在转动过程中，因支撑杆对平板的力矩沿板边方向，所以当两个动作电机工作时，产生的力矩互相垂直，由此可减少两向力之间的相互干扰，降低了系统控制时的耦合度。实体结构如下图1所示。

1.2.2 摄像头图传模块：OV2640

OV2640是OmniVision公司生产的1/4寸的CMOS UXGA（1632×1232）图像传感器;拥有200万像素和较大的可视区域，支持自动曝光控制、自动增益控制、自动白平衡、自动消除灯光条纹等自动控制功能。UXGA最高15帧/s，SVGA可达30帧，CIF可达60帧;并且支持DCMI传输和SCCB通信协议，是在诸多图传模块中性价比较高的一款摄像头。

1.2.3 动作模块：MG995数字舵机

在诸多电机中，在考虑成本的基础上可作为动作模块的电机大致可分为两种：舵机和步进电机。但由于步进电机的运动速度取决于细分并且可能存在丢步现象，因此其稳定性和响应速度都不及舵机，而舵机中SG90系列舵机（小蓝舵机）与数字舵机相比，虽价格低廉，但其稳定性和扭矩都较低因此满足不了控制系统的要求，所以我们选择了GM995数字舵机。

1.2.4 电源模块：航模电池连接可调式稳压模块

由于动作模块我们选择的是舵机，所以我们的电源模块需要满足舵机4.8～7.2V的工作电压，主控芯片上的电压虽然可以满足舵机的运行电压，但是板载电源并不能支持舵机运转，所以只能用外接大电流的航模电池连接稳压模块对舵机进行供电。

2  板球的控制系统

如框图2所示，该系统由数据获取装置、控制器、执行器、球和平板组成。

具体的工作方式为：小球在板上运动，摄像头将实时捕捉到的小球位置传给单片机，单片机经过数据处理后，会解算出相应的预期脉冲（占空比），以此来控制舵机转角，从而改变小球在板上的位置。

2.1 PID的控制算法

2.1.1 概念与选择

PID总结来讲就是对系统预期值所产生的偏差进行补偿的一种控制过程。

其控制公式为：

其中P为偏差比例，I为偏差积分，D为偏差微分。大致有位置型、增量型、积分分离型、抗积分饱和性、梯形积分型和变积分型几种类型。

在本次实验中我们应用的是变积分型PID，在普通的PID（如位置型）中积分常数ki是不变的，这就导致在系统的积分值偏差较大或较小时，积分常数会成为系统反应速度滞后的影响因素，而变积分的基本思想就是改变积分项的累加速度：偏差越大积分越小、偏差越小积分越大。因此变积分型PID具有较高的系统稳定性，符合本系统的核心要求。

2.1.2 算法的设计与实现

系统采用速度内环、位置外环的双闭环控制模式（模式如图3所示）。在板球系统运行过程中，位于上方的摄像头模块将实时扑捉到的小球位置反馈到单片机中，单片机会及时计算出预期位置，与摄像头传回的坐标进行比较得出位置差，作为位置外环，而通过位置差则可以计算出内环所需的速度差，进而做到PID双闭环控制，从而调整所输出的PWM脉冲，以弥补误差、增強系统稳定性。

3  图像的获取与处理

图像在获取的过程中，由于外界环境的干扰以及摄像头本身质量的原因，会造成获取后的图片模糊、部分缺损等。因此我们要对获取后的图像进行灰度处理、滤波、校正等处理。

3.1 灰度处理及二值化

由于摄像头输出的是24位真彩色图像，而为了对图像进行二值化，因此要先对图像进行灰度处理，即RGB色彩分量不等的将彩色图像转换为RGB色彩分量全部相等的灰度图像。我们通过平均值法，将彩色图像中的三分量亮度求平均值得到灰度值，公式如下：

Gray（i，j）=（R（i，j）+G（i，j）+B（i，j））/3

接下来为便是将灰度图像进行二值化，我们采用的是迭代阈值分割算法，步骤如下：

（1）设定一个阈值参数a。

（2）求出图象的最大灰度值和最小灰度值，分别记为Graymax和GrayPmin，令初始阈值T=（Graymax+GrayPmin）/2。

（3）根据阈值T将图象分割为两部分，分别求出两部分的平均灰度值Gray1和Gray2。

（4）求出新阈值T=（ Gray1+Gray2）/2。

（5）若新阈值T>a，即重复步骤3和步骤4，迭代计算，直到求出来的阈值T

3.2 滤波

由于器件本身的原因，获取图像时可能会引入了大量噪声，从而引起图像失真，造成最后计算出的坐标值有偏差，或在运行过程板子中抖动较大导致小球跑出视野范围造成目标丢失，这些因素都可能会造成系统超调甚至跑飞，因此我们需要对获取的数据进行滤波处理。

本实验我们应用了比较常见的滑动窗口滤波，因为小球位置的图传数据是实时传输的，数据量较大，而且具有较高的连续性，数据波动较小，滑窗滤波利用数据移动求均值的方法，能够以阶梯形式将原来数据进行平滑整合，滤除效果较好，能够保证有效数据的完整性，提高整个系统的稳定性。

4  程序的优化

首先我们假设摄像头所传回的数据通过滤波算法后，我们所得到的是一个“干净的”128mm×128mm的图像。常规的判断是从边界的一角进行全局扫描，进行判断小球的位置，然后将小球的位置带入双闭环控制系统中做出后续的控制响应。

然而我们所设计的优化方案则是：首先从所得到中点出发向四周进行扫描，快速得到第一次小球的位置，将此时小球的位置记录，随后在下一次的图像传回后将上一次所记录下的坐标作为起始点开始向四周扫描得到本次小球的位置，再次记录，如此循环往复。如图4所示。

5  结语

本文介绍了系统的基本构成概况，包括机械结构和硬件的选择构成。比较了几种常见芯片的优劣性，对所选择硬件的原因做出了解答。同时，对所选用的变积分型PID算法、摄像头阈值处理和滤波方式也进行了详细的介绍。

将优化的新算法与常规算法均写入操作系统进行对比，通过实际成品操作，经过大量实验后发现在同样的硬件条件下，优化后的板球控制系统更加稳定，其程序运行的占用深度参数也明显要比常规算法的占用深度参数低，说明优化后的程序解放了大量的后台运算空间，而由于起始扫描坐标与小球的实时坐标不会出现距离过远的情况，减少了误扫描出现的可能性，所以在某种意义上系统进行了“二次滤波”，系统的稳定性和反应速度也得到了明显的提高，不会在出现程序失调或跑飞的现象。该方案在理论研究以及实验操作中切实可行有效。

参考文献

[1] 王赓.基于视觉系统的板球控制装置的设计与开发[D].清华大学，2004.

[2] 张世奇.模糊自校正串级PID板球控制系统设计与研究[J].自动化技术与应用，2019，38（1）：1-4.

[3] 李玉衡，徐夏怡，宫瑶，等.基于串级PID和复合滤波算法板球控制系统设计[J].软件，2020，41（2）：1-7.

[4] 高多.板球系统的定点与轨迹跟踪控制器设计[D].东北大学，2016.

[5] 焦新杭，付建，陈佳磊，等.基于机器视觉的板球控制系统设计与实现[J].湖北理工学院学报，2019，35（4）：13-17.