具有时变时滞的奇异切换系统的指数稳定和L2 增益分析

李祉含 王 傲

（东北大学，辽宁 沈阳110819）

众所周知，奇异系统的分析和设计方法在理论和应用上越来越重要。20 世纪80 年代以后，奇异系统的研究进入了一个蓬勃发展的阶段，特别是在系统稳定性、可控性等方面的研究取得了许多重要成果。奇异系统比非奇异系统涉及更复杂的问题。首先，我们需要研究系统的稳定性和脉冲问题[1-3]。

近年来，切换系统与奇异系统相结合的研究逐渐深入[4-6]。切换系统是一种与实际问题相关且经常出现的混合系统，切换系统是在许多领域中，在动态过程中某一时刻的突然变化往往会导致脉冲行为，在这种情况下，研究具有脉冲的切换系统具有一定的意义[7,8]。

本文采用平均驻留时间和李雅普诺夫函数方法验证了系统的稳定性，并设计了状态反馈控制器。第三节，给出指数稳定的充分条件。第四节，研究了一类奇异系统的加权L2增益。

1 准备知识

考虑下面广义切换时变时滞系统

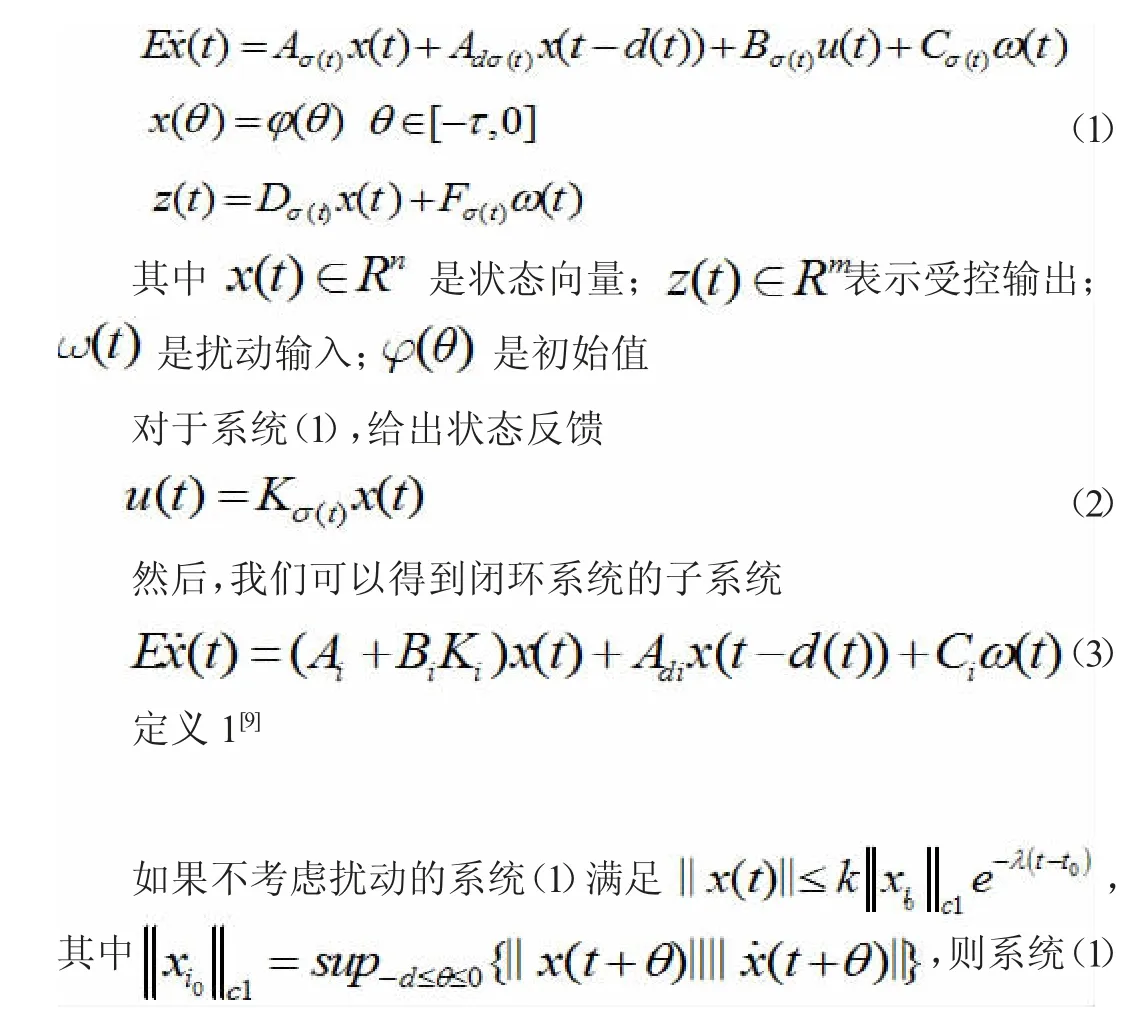
2 稳定性分析

2.1 定理1

则系统（1）是指数稳定的。

2.2 证明

选择李雅普诺夫函数

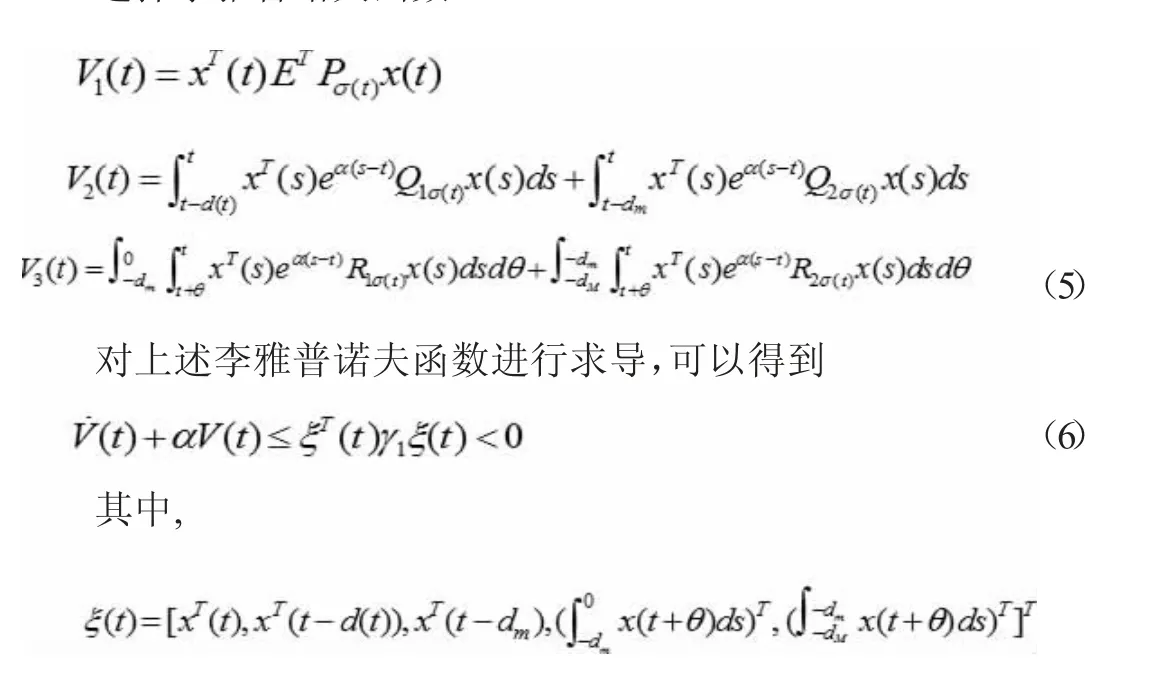
对于（6）式左右两侧进行积分，并结合平均驻留时间方法便可证明系统（1）是全局一致指数稳定的

3 增益分析

3.1 定理

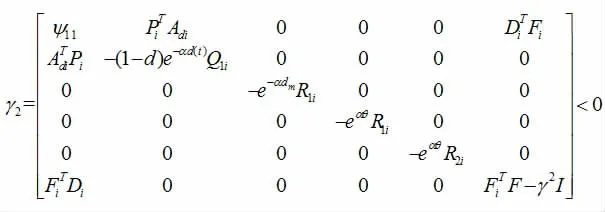
则系统有加权L2增益

3.2 证明

4 结论

针对一类带脉冲的奇异切换系统的指数稳定和L2增益问题。 首先，利用李雅普诺夫函数函数讨论了系统的稳定性。其次，我们提出了保证系统指数稳定性和加权L2增益的充分条件。