国内硫磺价格多元回归分析及验证

2020-08-13李大念

石油化工技术与经济 2020年2期

李大念

(中国石化炼油销售有限公司，上海 200050)

硫磺是基础化工原料，主要用于硫酸、磷肥、钛白粉、二硫化碳、己内酰胺、溴素、制糖等行业。我国是硫磺净进口国，对外依存度高达65%，主要货源来自中东、北美等地区。影响硫磺的价格因素主要有到岸价、港口库存量、原油价格以及下游硫酸、一二铵的开工率和价格等。多元回归分析是定量分析中最为常用的方法，通过探索数据之间的客观规律，把所要研究的对象以数学方程式的形式表现，并建立计量模型[1-2]。

文章选取硫磺到岸价、港口库存、原油价格等6个变量，以2016—2018年的数据为样本，运用Excel进行多元回归，获取价格回归模型。实证模型中多个解释变量之间可能有一定的相关关系，而这些相关性会影响回归结果的无偏性和有效性[3]。运用回归模型可以预测将来硫磺价格走势。

1 多元回归分析法

多元回归分析是定量分析中一种常用的方法，它是通过探索数据之间的客观规律，把要研究的对象以数学方程式的形式描述，建立数学模型。常见的多元分析有一个因变量、多个自变量等。

Y=b+β1X1+β2X2+β3X3…+βnXn

式中：Y为因变量，X1、X2、X3…Xn为自变量，b为常数项，β1、β2、β3…βn为回归因子。

根据最小二乘法，回归因子为：

β=(XXT)-1XYT

式中：β=[b,β1、β2、β3…βn]T

Excel多元回归主要工具，输出结果包含3部分。

(1)回归统计表

①Multiple R，复相关因子，是R2的平方根，又称为相关因子，用于衡量变量X和Y之间相关程度大小。

②R Square，复测定因子R2，说明自变量解释因变量变差的程度，以测定因变量Y的拟合效果。

③Adjusted R Square，调整复测定因子R2，衡量加入独立变量后模型的拟合程度。当有新的独立变量加入后，即使这一变量同因变量之间不相关，未经修正的R2也要增大，修正的R2仅用于比较含有同一个因变量的各种模型。

④标准误差，用来衡量拟合程度的大小，也用于计算与回归相关其他统计量，此值越小，说明拟合程度越好。

⑤观测值，用于估计回归方程的数据观测值个数。

(2)方差分析表

方差分析表通过F检验判断回归模型的回归效果。表中“回归分析”行计算的是估计值与均值之差的各项指标，“残差”行用于计算每个样本观察值与估计值之差的各项指标，“总计”行用于计算每个值与均值之差的各项指标。第二列df是自由度，第三列SS是离差的平方和，第四列MS是均方差，它是离差的平方和除以自由度，第五列是F统计量，第六列Significance F是在显著性水平下的Fα的临界值。

(3)回归参数表

主要是标准误差、t统计量和p值。

2 变量选取与样本数据

2.1 选择变量

针对影响硫磺价格的因素，选取进口到岸价、原油价格、港口库存量以及下游硫酸、磷肥价格等6个自变量，硫磺价格Y作为因变量。

(1)到岸价X1。中国是硫磺净进口国，对外依存度65%，主要货源来自中东、美国、俄罗斯、哈萨克斯坦、日本、韩国等，自合同签订后大约一个月之后到达国内港口，对国内现货市场价格影响较大。

(2)港口库存量X2。国内除中国石化供应量较大外，中石油、地炼等硫磺供应量小，因此，港口库存量对现货交易价格影响较大。

(3)原油价格X3。硫磺来自原油和天然气，原油价格变化对硫磺价格影响较小，选取WTI原油价格作为自变量X3。

(4)硫酸价格X4。硫磺作为原料用来生产硫酸，因此硫酸价格高低对硫磺市场价格有一定的影响。

(5)一铵价格X5。磷酸一铵价格变化直接影响硫磺市场价格波动。

(6)二铵价格X6。二铵市场价格波动直接影响硫磺原材料价格变化。

2.2 样本数据

选取2016—2018年的数据，具体见表1。

表1 2016—2018年硫磺价格及影响因素统计

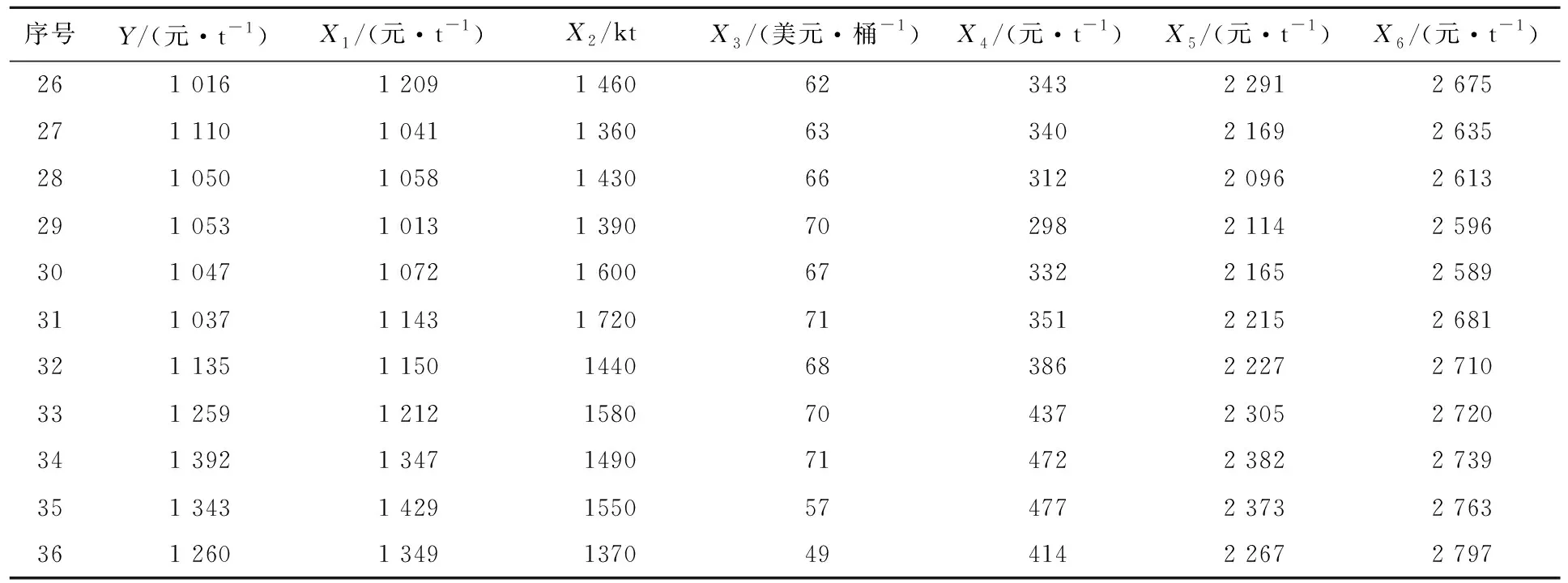
续表1

假设硫磺价格多元回归方程式为：

Y=b+β1X1+β2X2+β3X3+β4X4+β5X5+β6X6

2.3 多元回归

针对采集样本数据表1，运用Excel进行多元回归，可以发现到岸价、港口库存量、原油价格等6个因素对硫磺价格的影响大小。回归统计表中，R=0.970 3，表明硫磺到岸价等6个自变量X与硫磺价格因变量Y之间的关系为高度正相关；R Square复测定因子为0.941 5，表明用自变量X可解释因变量Y的94.15%；Adjusted Square调整后的复测定因子为0.929 5，说明自变量能够说明因变量Y的92.95%，因变量Y的7.05%要由其他因素来解释。标准误差为61.606 6，数值较小，说明拟合程度较好。

在方差分析表中，Significance F的P值为1.498 67×10-16，小于显著性水平0.05，说明硫磺价格多元回归方程效果显著，方程中至少有一个回归系数显著不为0。

回归参数表中，常数项b值为620.567 8，B18：B23为回归因子β1、β2…β6的值，多元回归方程式为：

Y=620.567 8+0.447 6X1-2.187 0X2+1.036 2X3+0.797 1X4+0.342 0X5-0.297 5X6

在E列中E18：E23为回归因子t统计量的p值，β2的t统计量p值为0.003 4，远远小于0.05，说明自变量X2与因变量Y相关性最强，即港口库存量对国内硫磺价格影响最大。β1、β4、β5、β6的t统计量p值为0.015 5、0.031 4、0.019 0、0.022 9均小于0.05，说明自变量X1、X4、X5、X6与因变量Y相关性较强，但是比X2差。β3的t统计量p值为0.567 3，大于0.05，说明自变量X3与因变量Y不存在相关性，该回归系数不显著，即国际原油价格对硫磺价格影响不显著。