加固岩体的预应力锚索拉力松弛分析模型

肖世国，曹顺利，赵琳智

(1.西南交通大学地质工程系, 成都 610031；2.西南交通大学高速铁路线路工程教育部重点实验室, 成都 610031)

预应力锚索具有布设灵活、工程适应能力强等诸多优点, 在岩土加固工程实践中得到广泛应用.然而，由于存在锚索拉力松弛效应，致使其拉力随时间发展比初始值有一定程度的减少或损失[1-6]，对实际锚固工程的长期稳定性产生重要影响.因此，合理分析锚索拉力随时间的变化规律对岩土锚固工程具有重要的实际意义.以往很多学者从不同角度对这一问题开展了研究，丁多文等[7]基于岩体的黏弹性特征，采用Kelvin体(简称K体)和Hooke体(简称H体)串联模型模拟其流变特性，推导了锚索应力损失计算公式；周永江等[8]考虑钢绞线的松弛率、灌浆材料的徐变损伤和岩体的流变特性，在一定程度上分析了锚索预应力损失机理；李英勇等[9]基于岩体的流变特性和锚索的松弛特征，采用多元件并联的四参数模型分析锚索应力变化；朱晗迓等[10-11]、景锋等[12]、王清标等[13]、邓东平等[14]也均考虑了锚索与岩体的相互作用，但采用模拟锚索的H体和模拟岩体的Kelvin-Hooke体(简称K-H体)的并联模型，计算分析锚索应力损失.王国富等[15]分别采用2个与3个参数模拟锚索与岩体性质，建立了五参数的并联分析模型.除了在理论分析方面的这些研究外，张发明等[16]、陈沅江等[17]均基于现场实测数据，对锚索应力损失问题进行了分析；此外，王克忠等[18]、范卫琴[19]还采用数值模拟的方法，研究讨论了锚索应力损失规律.因此，以往的相关研究对认识预应力锚索的拉力损失问题有重要意义.

大量的现场监测或室内试验研究结果表明[2-4,12,17-18]，对于预应力锚索加固的岩体工程，因岩体随时间逐渐产生流变特征[20]，而在这个过程中，又因锚索与岩体紧密黏结，导致锚索拉力降低而产生松弛，而受到降低的拉力作用的岩体仍会进一步产生流变，进而使锚索产生松弛，如此即形成岩体的流变与锚索的松弛变形之间的相互影响.因此，在岩体受外力作用稳定的情况下，岩体流变与锚索松弛之间必然产生相互耦合作用，这就是造成锚索拉力随时间逐渐损失的主要原因，并且锚索拉力一般具有衰减到一定程度而逐渐稳定的特征.在岩体流变与锚索松弛的相互耦合作用过程中，根据作用力与反作用力原理，岩体所受作用力和锚索所受作用力是相等的，然而，因二者的变形模量不同，所以二者的变形并不相等.

因此，以往的相关研究尽管可以在表现上一定程度地反映锚索拉力随时间逐渐衰减稳定的特征，但是这些研究在内在的岩体与锚索相互作用机理方面还尚未充分合理体现，特别是在反映锚索与岩体相互作用的分析模型方面还存在较多问题.其中典型的问题主要有：

1)对于以往研究较多采用模拟锚索的H体和模拟岩体的K-H体的并联模型，从模型本身反映的特征来看，意味着锚索的变形和岩体的变形相一致，但这显然不符合实际二者相互作用原理；或者，在考虑锚索周围岩体流变性的同时又将锚索等效为同一范围的弹性岩体[11]，存在锚索周围同一范围岩体性质矛盾的假定.

2)单一流变模型均有其适用的局限性，因而不考虑围岩与锚索相互作用特征而简单采用K体与H体的串联模型或者Maxwell体与K体的串联模型，并不能充分或合理反映锚索和岩体的特性以及二者间的相互作用机制.

因此，本文主要从锚索与岩体相互作用的宏观基本原理与特征出发，考虑锚索的线弹性特性和岩体的流变特性，建立预应力锚索内锚固段的锚索与岩体相互作用分析模型，以计算分析预应力锚索的拉力松弛或损失问题.

1 模型建立

假设锚索间距相对较大，不计群锚效应.对于单根锚索的锚固岩体，在锚索拉力作用下，锚固体与锚孔周围的岩体(简称围岩)之间的界面会产生摩阻力.从整体力学作用效果来看，可视为该摩阻力使得围岩整体产生“拉拔效应”，围岩整体承受的“拉拔力”等于锚索拉力.同时，在这个过程中，锚索的拉伸应变并不等于围岩的拉伸应变，而锚索-围岩体整体的拉伸变形则由锚索和围岩各自拉伸变形之和组成(即锚索相对于围岩的变形+围岩自身变形).若认为砂浆性质与围岩相同，则可以采用如图1(a)所示的H体和K-H体的串联模型来描述锚索与围岩之间的这种相互作用关系.其中：T为锚索拉力；Ea为模拟锚索性质的H体的弹性模量；Erk、Erh和η分别为模拟围岩流变性质的K-H体的2个弹性模量和1个黏滞系数.本模型是H体和K-H体的串联，而后者又具有收敛变形的特征[21-22]，因此，本模型仍可保证在两侧拉力作用下模型变形收敛的基本特征.图1(b)所示的模型为以往研究所提出的并联模型[10-15]，其反映的一般含义是锚索所受作用力与围岩所受作用力不同但二者的变形(应变)却相同.由两模型对比可见，本文模型将反映锚索性质的H体与反映围岩性质的K-H体串联，可更加合理地反映锚索所受作用力与围岩所受作用力相同而二者的变形(应变)却不一定相同的实际情况和锚索与围岩间的基本相互作用特征.

2 分析推导

根据图1所示的锚索与围岩相互作用分析模型,在不考虑降雨、坡体滑动等外部因素对锚索变形影响的条件下，锚索拉力T和模型总的拉应变ε之间可建立方程

(1)

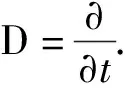
对于松弛问题，有ε=常量(即Dε=0)，于是，式(1)两侧同乘以AaArEaErhErk，再经通分后可化简得(限于篇幅，省略详细推导过程)

(2)

式中系数λ1、λ2、λ3分别等于

λ1=ArErhη+AaEaη

λ2=ArErhErk+AaEaErh+AaEaErk

λ3=AaArEaErhErk

解式(2)所示的微分方程，可得

(3)

式中：t为时间；C为积分常数.

由初始条件T(0)=T0，式(3)可写成

(4)

需要说明的是，式(4)中的应变ε可根据锚索初始拉力确定，即

(5)

由此，可根据式(4)确定锚索拉力随时间t的松弛变化规律.同时，结合图1进一步可见，相比以往的串联模型，本文模型涉及的参数个数与取值方法均与以往相同，但在模型原理和锚索松弛拉力计算分析方法上与以往不同.

3 实例验证

3.1 室内模型试验

以陈安敏等[3]的室内模型试验为实例，进行对比分析.模型尺寸为80 cm×80 cm×80 cm，锚索模拟材料用φ6×2 mm的铜管，弹性模量Ea=1.32×105MPa，围岩采用黄黏砂土材料模拟，模型布置尺寸如图2所示.

以其中的编号为第2、3组的蠕变试验为例，在试验应力水平下(按照文献[23]方法估算，模型锚索孔壁最大剪应力约为10 kPa)，通过室内试验得到蠕变曲线[11]，对其进行曲线拟合可得模型围岩(用K-H体描述其性质)的材料参数，如表1所示.可见，2组试验获得的参数较为接近，取其平均值近似作为模型围岩的材料流变计算参数.为便于后续对比分析，这里也列出文献[11]实际所采用的参数，即：Erh=9.362 MPa，Erk=7.719 MPa，η=607.795 MPa/h[11].可能因曲线拟合计算误差导致其结果与表1所给出的结果(2组平均值)略有差异，三参数的误差分别为2.6%、4.4%、11.7%，整体上可认为二者接近.

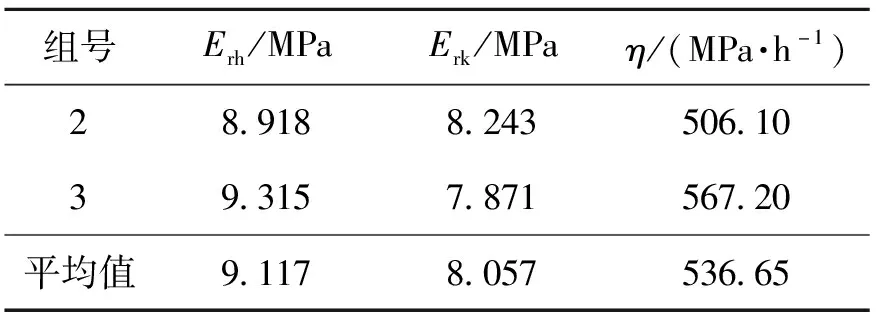
表1 模型围岩材料流变参数

这样，以其中初始拉力分别为53、81 N的2#、3#模型锚索的拉力松弛问题为例，将对应的参数代入式(4)中可得模型锚索的拉力随时间变化规律，如图3所示.同时，图3中还给出了试验结果和以往相关模型[11]的计算结果.可见，本文方法所得到的锚索松弛后的拉力终值与试验结果误差为6%，二者吻合较好，锚索拉力计算损失率约为50%(试验值为47%)，与朱晗迓等[11]所提出的模型的计算结果也较为接近.

3.2 现场试验

尽管图3显示本文方法及已有方法均与一室内试验结果吻合较好，但由于室内试验模型可能相对理想，有时难以充分说明问题.因此，这里以陈沅江等[17]的现场监测试验作为工程实例进一步分析.该试验依托湖南西部常张高速公路K123边坡工程，取其中的2根预应力锚索作为试验锚索，张拉吨位为600 kN，其中锚固体长25～30 m，锚索由4根高强度低松弛无黏结钢绞线组成，极限抗拉强度为1 860 MPa，直径为15.24 mm，锚索弹性模量取为195 GPa，锚孔直径为110 mm，锚孔间距取为3 m.现场测点布设如图4所示.

根据由现场试验测得的试验锚索周围岩体(如图4所示，距锚孔0.8 m)中的应力随时间变化曲线[17]，考虑现场测试的应力水平(按照文献[23]方法估算，锚索孔壁最大剪应力约为110 kPa)，基于室内蠕变试验结果，陈沅江等[17]给出了其岩体(用K-H体描述其性质)流变计算参数，如表2所示.

表2 现场围岩材料流变参数

于是，把相关参数代入式(4)中可得实际锚索的拉力随时间变化规律，如图5所示.同时，图5中还给出了现场测试结果和以往相关模型[11]的计算结果.可见，锚索松弛后拉力终值的计算与实测结果误差为7%；同时，现场测试结果显示锚索拉力损失率约为15%，本文方法计算结果约为10%，与其吻合较好，而采用朱晗迓等[11]模型的计算结果则为98%，与现场测试结果差异较大，明显与实际不符.因此，相对而言，本文的模型更具有合理性.

本文的模型是用K-H体模拟围岩的流变性质，因此，实际工程中对于围岩流变属性较为符合K-H体的情况，方可采用本文所提出的分析模型.对于缺乏现场试验条件的情况，应尽量采用室内试验的方法确定围岩的流变属性和描述其属性的流变模型，用之代替图1(a)中的K-H体模型部分，即形成对该实际问题的分析模型.根据以往相关试验结果[3,12,14,17]，K-H体在较多情况下可以描述锚索周围岩体的流变性质，因此，对于没有任何试验资料的实际问题，可采用本文所提出的模型进行估算，但要进一步确认相关分析结果，仍需进行现场或室内试验.同时，需要说明的是，由于本文方法将锚索外部的围岩视为均质体(实际并非均质体)且不计群锚效应，这些都会造成分析模型与实际原型之间存在一定的误差，尤其体现在开始时间阶段计算值与试验值差异偏大(见图3).

此外，需要指出的是，本文主要是针对单根锚索或者锚索间距较大的群锚，未涉及锚索之间相互影响.对于锚索间距较小的群锚问题，因存在群锚效应，锚索间围岩应力叠加将促进围岩蠕变，从而会进一步强化锚索松弛效应，故按本文方法估算的锚拉力松弛效应可能比实际偏弱(见图5).

4 参数分析与讨论

若将锚索张拉锁定后的任一时刻t的锚索拉力松弛率记为ξ(t)=T(t)/T0，则由式(4)及相关分析可见，锚索直径(截面积)、锚孔间距、锚索弹性模量以及围岩的3个流变参数均对ξ(t)有影响，下面依托3.2节中工程实例的基本参数，采用控制变量法，分别具体给出其影响特征.

1)锚索直径

图6给出了锚索直径对锚索拉力松弛率的影响曲线，可见，随着锚索直径的增大，在同一时刻锚索的松弛效应呈非线性增强.

2)锚孔间距

图7是锚孔间距对锚索拉力松弛率的影响曲线，可见，随着锚孔间距的增大，在同一时刻锚索的松弛效应呈非线性减弱.

3)锚索弹性模量

图8给出了锚索弹性模量对锚索拉力松弛率的影响曲线，可见，随着锚索弹性模量的增大，在同一时刻锚索的松弛效应呈线性增强.

4)围岩H体弹性模量

图9给出了围岩H体弹性模量对锚索拉力松弛率的影响曲线，可见，随着围岩H体弹性模量的变化，在同一时刻锚索的松弛效应几乎不变.

5)围岩K体弹性模量

图10是围岩K体弹性模量对锚索拉力松弛率的影响曲线，可见，随着围岩K体弹性模量的增大，在同一时刻锚索的松弛效应呈非线性减弱.

6)围岩K体黏滞系数

图11是围岩K体黏滞系数对锚索拉力松弛率的影响曲线，可见，随着围岩K体黏滞系数的增大，在开始时刻锚索的松弛效应呈较显著的非线性减弱，但随着时间的推移，这种变化特征不再明显，经过相对较长的时间后，该黏滞系数对锚索拉力的松弛效应几乎没有影响.

5 结论

1)可采用描述锚索力学性质的H体和描述围岩流变力学性质的K-H体的串联模型来整体描述锚索与围岩之间的相互作用关系，以此模型可确定锚索拉力的松弛方程.该方程表明，锚索的长期拉力主要受锚孔间距、锚索弹性模量、围岩的流变参数、锚索直径等重要因素影响.

2)锚索拉力的松弛效应随锚孔间距、围岩K体弹性模量的增大而呈较为显著的非线性减弱的特征，但随锚索直径与弹性模量的增大，分别逐渐呈非线性与线性增强的变化特征.围岩H体弹性模量对锚索松弛效应影响很小，而围岩K体黏滞系数在锚索张拉锁定后的较短时间内对锚索松弛效应有显著地非线性弱化作用，但其产生的影响随时间快速衰减.

致谢：感谢同济大学夏才初教授对本文研究工作给予的讨论与帮助.