基于萨道夫斯基公式分段修正的隧道爆破振动研究
2020-08-12徐言
徐言
(中交一公局集团有限公司,北京100024)
1 概述
随着我国经济的快速发展,高速铁路、高速公路等基础设施建设也迎来了快速的发展时期。隧道掘进工程因地层条件和岩石性质等复杂因素的影响,往往是高速铁路工程施工的关键性控制工程,其施工质量与施工进度情况严重制约着整个工程施工过程。在我国,大约有95%的山岭隧道开挖采用钻爆法进行施工[1]。在隧道掌子面进行钻孔、安放炸药而后爆破开挖的整个施工过程中,炸药爆炸产生的能量除了用于目标岩体开挖外,剩余的能量还会以振动波的形式向外传播,产生爆破振动灾害[2]。爆破产生的振动波会随着距离爆破位置的不断增加而逐渐减小,从最初的爆炸冲击波衰减为应力波进而衰减为弹性振动波,围岩体也在爆破冲击波、应力波和振动波的作用下产生围岩压碎带、裂隙带以及弹性振动带。围岩压碎与裂隙带构成开挖岩体,振动波则形成了一个有一定影响范围的爆破振动场[3]。若该场内存在一些构筑物,如民房、电塔等,爆破振动波作用在构筑物的基础与结构上,造成构筑物振动、损伤乃至破坏[4]。如何衡量爆破振动产生的影响及范围一直是工程爆破领域重要的研究方向之一。运用爆破振动波诱发的振动场内既有构筑物节点的振动速度或加速度作为爆破设计与施工安全的判据,是国内外学者在大量工程爆破和长期实践的基础上取得的共识[5]。但是,如何计算爆破振动速度,不同国家根据自身的试验总结出的经验公式形式不尽相同。

式中: K、α 分别为与工程爆破参数、岩石条件等有关的系数;Q为毫秒延时爆破中最大段装药量(kg);R 为爆心距(m);V 为监测的峰值振动速度(cm/s)。通过上述公式可以看出,萨道夫斯基公式中各项参数的物理意义明确,现场应用起来也较为方便,通过现场爆破参数与峰值振动速度的获取可为爆破设计提供理论依据,因此,该方法至今仍是各种工程爆破参数设计与优化重要依据。众所周知,工程爆破是炸药在化学反应后作用在岩体上的一个极其复杂的过程,且施工过程中隧道的地层条件和围岩等级也是在不断变化的,而萨氏公式中仅考虑了装药量、爆心距离等主要参数,围岩条件、地形参数、装药结构等参数都未能加以考虑,爆破振动速度与这些参数和条件之间存在着极其复杂的非线性关系,因此就会导致采用萨道夫斯基公式进行振动速度拟合过程中出现拟合精度不够等问题。基于上述分析,本文将针对现场实际的监测数据本文针对萨道夫斯基公式进行分段线性拟合研究,使其拟合精度更高,为隧道工程爆破振动分析提供数据支撑。
2 工程背景与现场监测
2.1 工程概况。三棱山隧道是京沈客专线路上重要的隧道工程,隧道位于辽宁省阜新市阜新蒙古自治县紫都台乡南部。隧道全长8888m,最深处的最大埋深为217.56m,隧道为双向高铁线路隧道,隧道断面大,地层条件差,现场爆破施工需尽量控制爆破振动影响。
2.2 隧道爆破方案。隧道采用钻爆法进行施工,爆破炸药为2 号岩石乳化炸药,详细参数见表1 所示。爆破采用常规的爆破孔布置方式,即布置有掏槽孔、辅助孔、崩落孔、周边孔、底孔等爆破孔。其中,掏槽孔位于掌子面中下位置,采用楔形掏槽的方式进行布置。爆破孔间距大多为在0.5-0.7m,钻孔深度为3.0m,具体的爆破分段如图1 所示。采用预裂爆破以确保爆破质量和控制围岩损伤,因此周边孔(MS11)和拱顶孔(MS13)采用间隔装药,其余爆破孔采用不耦合装药,装药长度为2.5m。各段间采用毫秒延时的爆破方式进行,分段时间间隔如表2 所示。

表1 爆破参数
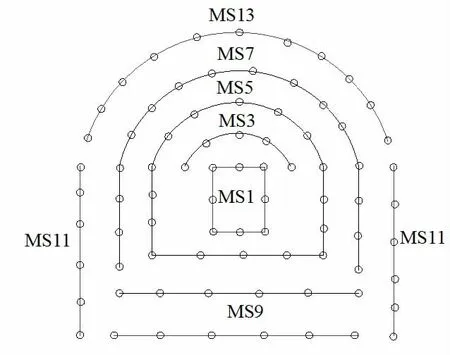
图1 爆破孔位置及分段情况示意图

表2 分段爆破的时间间隔
2.3 爆破振动监测
为了更好的研究爆破振动波的传播规律和其衰减规律,现场在爆破过程同步采用U-Box振动速度监测仪器对隧道爆破振动进行监测,为了提高监测效率,采用2-3 台U-Box振动速度监测仪按一定的距离线性布置同时对隧道章子面爆破振动速度进行监测,监测仪器及传感器布置方式见图2 所示。
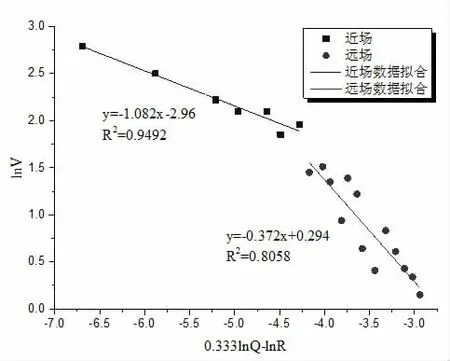
图2 U-Box 仪器及现场监测布置图
3 分段线性拟合修正的萨氏公式
通过大量监测,共选取了隧道内及隧道外山体上20 个距离章子面不同位置的爆破距离进行爆破振动监测,详细的监测信息与初步数据处理结果如表3 所示。
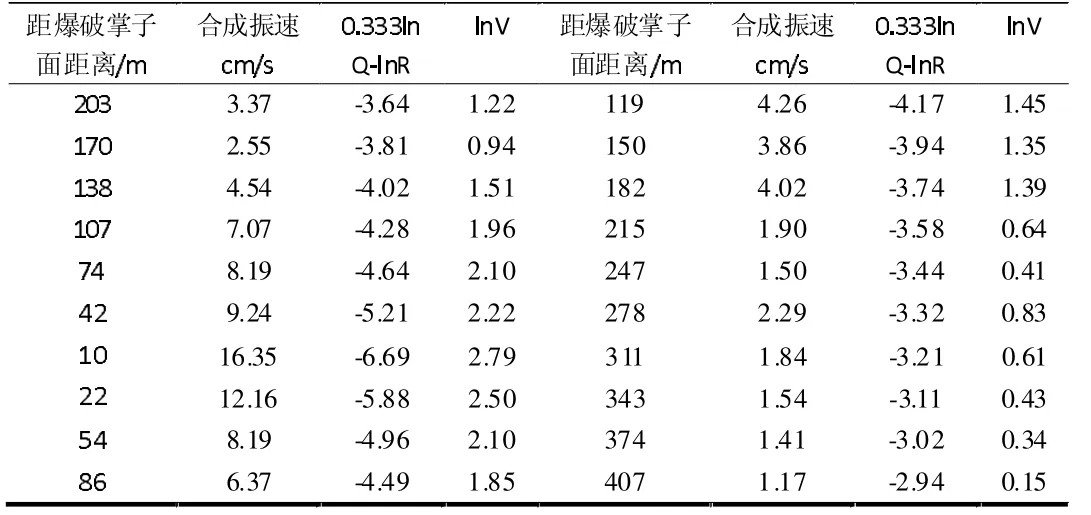
表3 不同距离振动场监测数据
采用公式(2)中的萨道夫斯基公式对现场20 组监测数据进行拟合,拟合结果见图3(a)所示,发现拟合精度很低,考虑到爆破振动波的衰减特性,本节创新性的采用了分段线性拟合的方式对监测数据进行了拟合分析,分段线性的拟合结果如图3(b)所示。
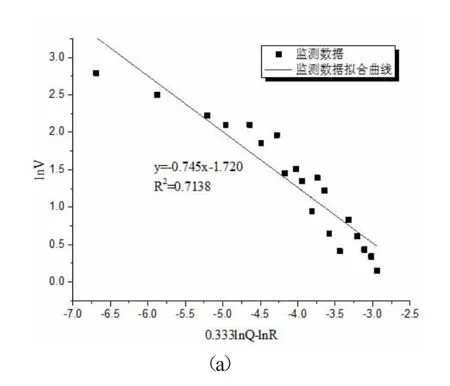
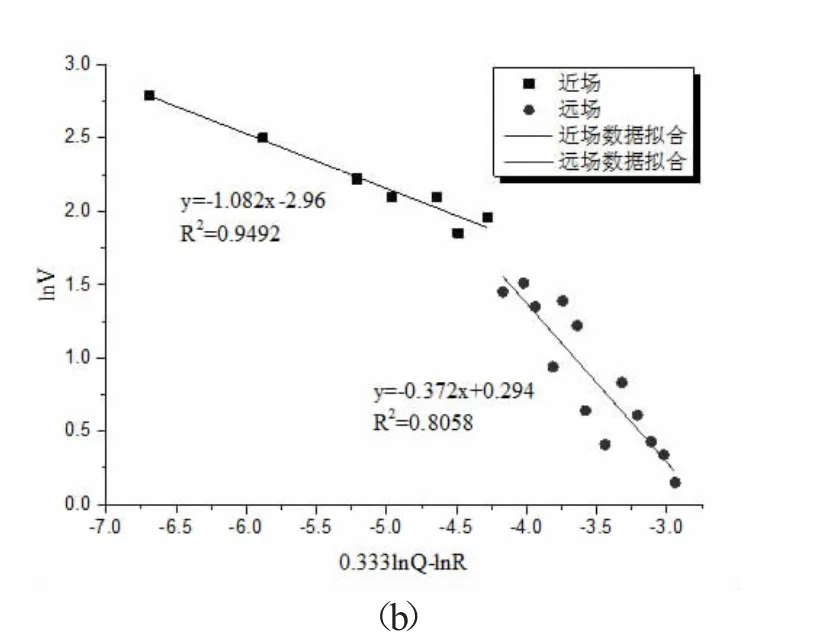
图3 隧道振动场监测数据的线性拟合图
如图3 所示,基于现场监测数据,无论是采用线性拟合还是分段线性拟合的方式进行拟合,都可知爆破峰值速度的变化规律与距离爆破掌子面间的距离有关。但是采用全部数据的线性拟合曲线可知其拟合精度较低,无法满足现场爆破振动预测与炸药参数优化的需求。从可用于指导现场实际工程的需求出发,将距离不同爆破章子面的距离划分成两类,分别定义为近场和远场,根据监测数据分析可知,近场与远场间的分界距离为110m,图3(b)中两组数据(蓝色与红色)分别代表两组采用萨道夫斯基公式进行分段拟合的线性关系。通过数据分析可知,对于近场的监测数据拟合结果曲线比较平缓,拟合效果非常好,拟合精度高达95%,斜率α=1.082,截距lnK=2.96,K值为19.3。对于远场的监测数据拟合结果曲线比较陡,拟合效果也有所提高,拟合精度为81%,斜率α=0.372,截距lnK=0.294,K值约为1.23。总体结果反映出近场爆破峰值振速随距离增大衰减较慢,而远场爆破峰值振速随距离增大衰减较快。
4 结论
本文针对隧道爆破振动灾害问题进行了系统分析,取得如下研究成果:
4.1 本文通过文献调研,列举了我国《爆破规程》中推荐的萨道夫斯基公式,并总结归纳了其优点与存在的潜在问题,提出了可采用分段线性拟合的方式对其进行修正以提高拟合精度。
4.2 以三棱山隧道工程爆破施工为背景,采用U-Box振动速度监测仪器,开展了20 组爆破振动峰值速度监测,获得距离爆破位置不同距离的爆破振动监测数据。
4.3 针对采用传统萨道夫斯基公式拟合精度不够的问题,本文创新性的采用了分段线性拟合的方式对监测数据进行了拟合,界定了爆破振动灾害的近场与远场,并总结提出各自对应的振速衰减特征。
