特征与分类算法在基于肌音信号的头部运动分类中的对比研究

章 悦，夏春明，谢佳智，刘 爽

（华东理工大学机械与动力工程学院，上海，200237）

引 言

肌音信号（Mechanomyogarphy, MMG）是一种生物医学信号，用于记录肌纤维收缩时的力学振动特性[1]，近些年来已逐步广泛应用于动作模式识别研究。相比于MMG，之前在动作模式识别研究中使用更多的主要是表面肌电信号（Surface electromography,sEMG）。根据研究的不同特征，基于sEMG 的动作模式识别可分为4大类：时域分析、频域分析、时-频域分析和非线性动力学分析。时域分析是传统的信号分析方法，可提取均方根值（Root mean square, RMS）、方差（Variance, VAR）、过零率（Zero crossing, ZC）等特征。例如，马正华等[2]在对sEMG 提取RMS 等时域特征的基础上运用线性判别分析（Linear discriminant analysis,LDA），实现对6种手势的有效识别，且识别率高达94%以上。频域分析是通过Fourier变换等方法将时域信号转换为频域信号，从而对信号的频谱提取特征，如平均功率频率（Mean power frequency,MPF）和中值频率（Middle frequency,MF）等[3]。时-频域分析是将时域与频域两者结合起来的方法，可在此基础上提取特征，例如在小波包变换的基础上提取小波包能量、小波包分解系数的奇异值等。Hu等[4]在两种肢体动作的分类研究中，使用sEMG 的相对小波包能量作为特征，实现对前臂内侧旋转和外侧旋转两类动作的模式识别。非线性动力学分析则是对于少数变量的单一时间序列提取整个系统的动力学特征，包括各种熵、Lyapunov指数和复杂度等。例如张启忠等[5]在提取分形维数和近似熵（Approximate entropy,Ap-En）两种非线性动力学特征的基础上，提出一种具有增量学习能力的K 近邻（K-nearest neighbor,KNN）模型增量学习算法作为模式识别的分类器，实现对4类手腕动作的识别，识别率达到92.5%。

由于MMG 采集比sEMG 更加方便，故在一些研究中可作为EMG 的辅助或替代工具[6-7]，甚至在某些特定的研究中具有一定的优势[8]，基于MMG 的假手控制方面的研究已取得一定的进展[9-10]。Zeng等[11]对于MMG 提取绝对MAV 等时域特征以及MF，在主成分分析（Principal component analysis,PCA）降维的基础上使用二次判别分析（Quadratic discriminant analysis, QDA）算法，实现对4 类手部动作的模式识别。Xie 等[12]在基于MMG 的假手控制研究中，使用小波变换、奇异值分解以及基于距离评估准则的特征选择技术，实现4 类手部动作的模式识别。Ding 等[13]提取MMG 的小波包变换系数、平稳小波变换系数和频域混合特征3 类特征集，使用支持向量机（Support vector machine, SVM）训练后对5个手指动作的识别率可达到91%以上。Wu 等[14]在面向可穿戴下肢助力机器人或助力下肢假肢的膝部动作模式识别研究中，提出一种卷积神经网络（Convolutional neural network, CNN）与SVM 相结合的模型，用于处理4 通道MMG，对于6 种动作可达到94%的平均分类精度。

在临床上，许多四肢瘫痪患者（例如高位截瘫的脊髓损伤患者）的四肢运动功能重度丧失，但是他们的颈椎运动功能往往保存比较完整，可以完成一些简单的头部活动。采集颈部肌肉的MMG，提取小波包特征，并运用SVM 作为分类器可实现对于多类头部动作的模式识别[15]。为了进一步研究MMG 各类特征及分类器算法与头部运动的分类准确率之间的关系，本文选取各种时域、时-频域和非线性动力学特征建立的高维特征矢量，以及使用SVM，KNN 和LDA 这3 种在基于MMG 或sEMG 的模式识别中较常见的算法，并根据交叉验证（Crossing verification, CV）结果探究不同特征组合或分类器与头部动作MMG 的分类准确率之间的关系。

1 特征提取与组合

如上，时域、频域、时-频域和非线性动力学等多种特征在各种基于MMG 或sEMG 的模式识别研究中已得到广泛应用。这些特征具备不同的物理意义，从不同方面对信号特性进行了表征。在之前的研究中，单独使用时域特征、时-频域特征或非线性动力学特征时均取得过较好的分类效果。

1.1 时域特征

时域分析在时间维度上反映信号的特性，是传统的sEMG 或MMG 分析方法。将信号看作时间的函数，通过时域信号分析可得信号的一些统计特征。本文选用RMS，VAR，ZC，改进的平均绝对值(Modified mean absolute value, MMAV)，波形长度 (Wave length, WL)和 log detector (LOG)作为时域特征[16]。

1.2 时-频域特征

时频域特征选用的是小波包（Wavelet packet, WP）结点能量，即对信号进行多尺度小波包分解，再根据一些特定频段计算结点能量。在本研究中，MMG 的采样频率为1 000 Hz，将信号分解到第i层，则MMG 信号在整个频域内被划分为2i个频带，每个频带宽为。由于MMG 较敏感的频带范围是5～60 Hz，故对MMG 进行6 尺度小波包分解（此处选取的是DB9 小波），并根据Parseval 定理计算小波包 6 层分解后其中低频段 6 个结点的能量（依次为 WP(6,1)，WP(6,3)，WP(6,2)，WP(6,6)，WP(6,7)和WP(6,5)结点[17]）作为时-频域特征。

1.3 非线性动力学特征

选取在基于sEMG 信号的模式识别研究中，非线性动力学分析中得到应用且效果较好的近似熵（ApEn）[5]、模糊熵(FuzzyEn)[18]和样本熵(SampEn)3 个特征[19]作为本文中的非线性动力学特征。ApEn是一种统计方法，表征了高维空间中矢量的聚集程度，使用一个非负数表示一个时间序列的复杂性，该非负数随着复杂性的增加而增大。SampEn 是对ApEn 的进一步改进，在计算时不包含自身数据段的比较，而是求取两个序列在相似容限r下匹配m个点与匹配m+1 个点两种概率之比的对数值。FuzzyEn则是对SampEn 的进一步改进，基于向量形状的近似性对时间序列复杂性和无规则程度的度量。

1.4 特征集的组合

将以上所有特征分为5 组特征集，如表1 所示。为了消除不同特征之间的量纲影响，需对各种特征值进行[0,1]范围的标准化。特征集的组合方式为：以选用特征集1+5 为例，将其合并为3（每个特征集中有3 个特征）×2（特征集1+5）×4（通道个数）=24 维特征。

1.5 特征降维

为去除特征集组合中的冗余信息，可使用特征降维方式，将特征从原始特征空间变换到一个维度较低的特征子空间中。本文使用基于方差的PCA[20]对特征作降维处理。对于归一化后的特征值用方差作为衡量，将所有特征值的总方差分解为不相关变量（主成分）的方差之和（个数维持不变），第k个主成分提取的信息占总信息的比重为第k个主成分的贡献率。前m个主成分的贡献率之和为累计贡献率，作为前m个主成分综合提供所有特征值信息的程度，本文中选择累计贡献率为95%。

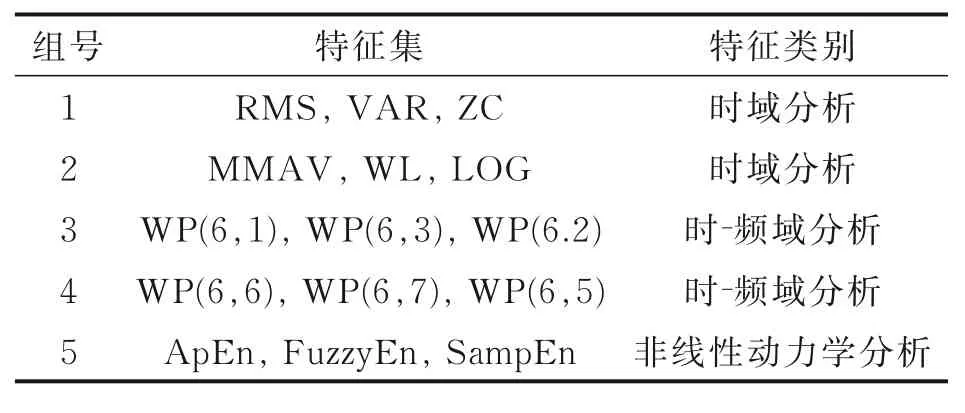
表1 特征集划分Table 1 Division of feature sets

2 分类器设计方法

2.1 支持向量机

SVM 是一种基于统计学习理论的模式识别方法，在特征空间中构造出最优超平面，使得超平面与不同样本集之间的距离最大，从而得到最大的泛化能力。SVM 在处理二分类问题时，线性判别函数的一般形式为f(x)=ω⋅x+b，对应的分类面方程为

将判别函数进行归一化，使所有样本都满足

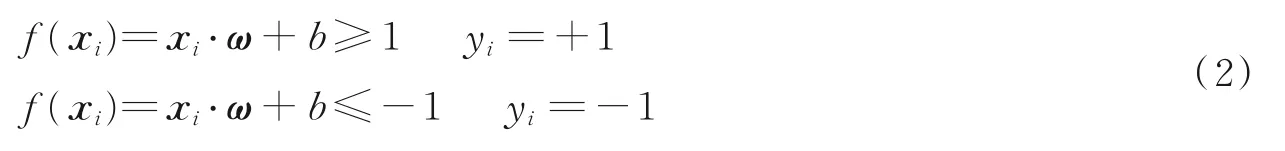
应用支持向量机解决多分类问题时，可在任意两类样本之间设计一个SVM，k个类别的样本总共设计个SVM。对于测试样本而言，最终得票最多的类别即为被判定的类别。本文中支持向量机选用径向基函数（Radial basis function, RBF）作为核函数，

2.2 K 近邻

KNN 是使用一种距离度量计算待分类样本与所有训练样本之间的距离，找到距离待分类样本最近的K个近邻；然后根据这K个近邻所属的类别进行投票，按投票数确定待分类样本的类别。由于KNN在类别决策时，只与极少数相邻样本有关，故该算法性能稳定且训练过程非常快。本文中采用的是欧氏距离[21]，并且取K为 9。

2.3 线性判别分析

LDA 将n类m维特征集尽可能地投影到一条直线或超平面上，使得投影后同类样本的样本方差尽可能小，而不同样本之间的方差均值之差尽可能大，从而使得类与类之间尽可能分开。对于m维特征向量，判别函数为

式中：W0=(ω1,ω2,…,ωm)T为权向量；X= (x1,x2,…,xm)T为模式向量；ωm+1为偏置项。当类别数n＞3 时，边界为超平面。当处理多类问题时，每类都有一个判别函数，要判别X属于哪个类，先计算n个判别函数

式中k=1,2,…,n。根据计算结果得出gk(x)最大的那个类就是X所属类别。

3 交叉验证分类精度的计算方法

对所有的动作进行标记：将点头、抬头、左摆头、右摆头、左转头和右转头分别标记为1 至6。K折交叉验证（K-CV）曾被用于sEMG 识别系统性能的评估[22]，即对于每个模式，将样本分为K组，每个子集分别做一次测试集，其余的K-1 组子集作为训练集，将最终由分类器识别测试集的结果与标记进行对比，如果一致就认为正确，否则认为错误。统计所有测试样本的识别率，如式（5）所示。

式中：AC 表示分类精度，Nr表示分类正确的样本个数，Na表示所有测试样本个数。用K个模型验证集分类准确率的平均数，即交叉验证精度作为K-CV 下分类器的性能指标，即

式中：k为使用的折数，Ak是每一个折的分类精度。本文中采用5 折交叉验证，即将每类动作的100 个样本平均分为5 个折（每折为20 个样本），其中1 个折作为测试集，其余4 个折用于训练分类器，再对测试集进行识别，获取分类准确度，从而评估分类器在实际使用时的泛化能力。

4 实验与结果分析

4.1 实验设备与方法

在本文研究中，8 名无神经肌肉疾病史的成年男性学生（年龄为24.4±0.9 岁，身高为175.6±4.0 cm，体重为64.1±5.8 kg）自愿参与这次实验。他们对于实验的内容完全知情，并且在实验前24 h 未从事剧烈运动。

实验过程中，要求受试者完成低头、抬头、左摆头、右摆头、左转头和右转头共6 类头部动作[15]。每类动作做100 下，每个动作之间间隔3～4 s。为了避免肌肉疲劳的影响，每类动作完成后休息30 min，再进行下一类动作，直到把6 类动作都做完。

采集颈部肌肉的MMG，使用医用无纺布在颈部左右两侧的胸锁乳突肌和头夹肌4 个部位[23]分别粘贴一个MMG 传感器。所选的传感器为加速度传感器，由于MMG 的主要信号能量在低频段（5～100 Hz），因此所选的传感器应在此低频段有很好的响应能力。另外为减小传感器质量对采集信号的影响，选择质量较轻的传感器。采集设备为美国国家仪器公司的NI 9205 采集卡，设置采样频率为1 000 Hz，使用一个增益为2 000 的放大器对MMG 信号进行放大处理。原始肌音信号中包含了运动伪迹及工频干扰等，在提取特征前需要进行预处理。对原始MMG 使用49.9～50.1 Hz 的带阻滤波器消除50 Hz 的工频干扰，再使用5～100 Hz 的数字滤波器进行带通滤波。数据分析在笔记本电脑安装的MATLAB 软件上执行。

由于每个动作的信号长度不等，所以采用一种离线处理的不等长分割算法以获取每个动作对应的MMG[24]。在获得每个动作对应的四通道信号后，对其提取上文提到的15 个特征。在对特征集进行组合的基础上，对高维特征矢量进行PCA 降维处理，再分别使用以上3 种算法针对各种组合特征集计算分类精度。

4.2 实验结果与分析

分别选取一组、两组和三组特征集进行组合，并将每种组合后的高维特征矢量在降维后分别使用SVM，KNN 和LDA 3 种分类器对6 种动作进行模式识别，获得的分类精度如图1—3 所示。

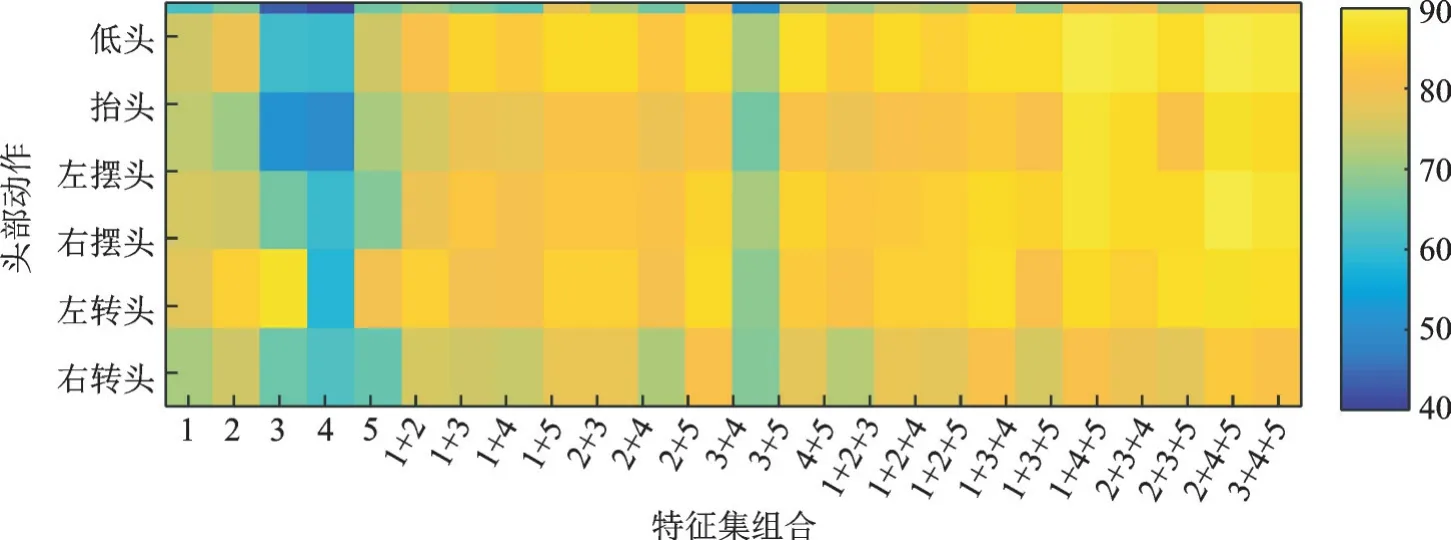
图1 使用SVM 的交叉验证分类精度色块图Fig.1 Color block diagram of cross validation classification when using SVM

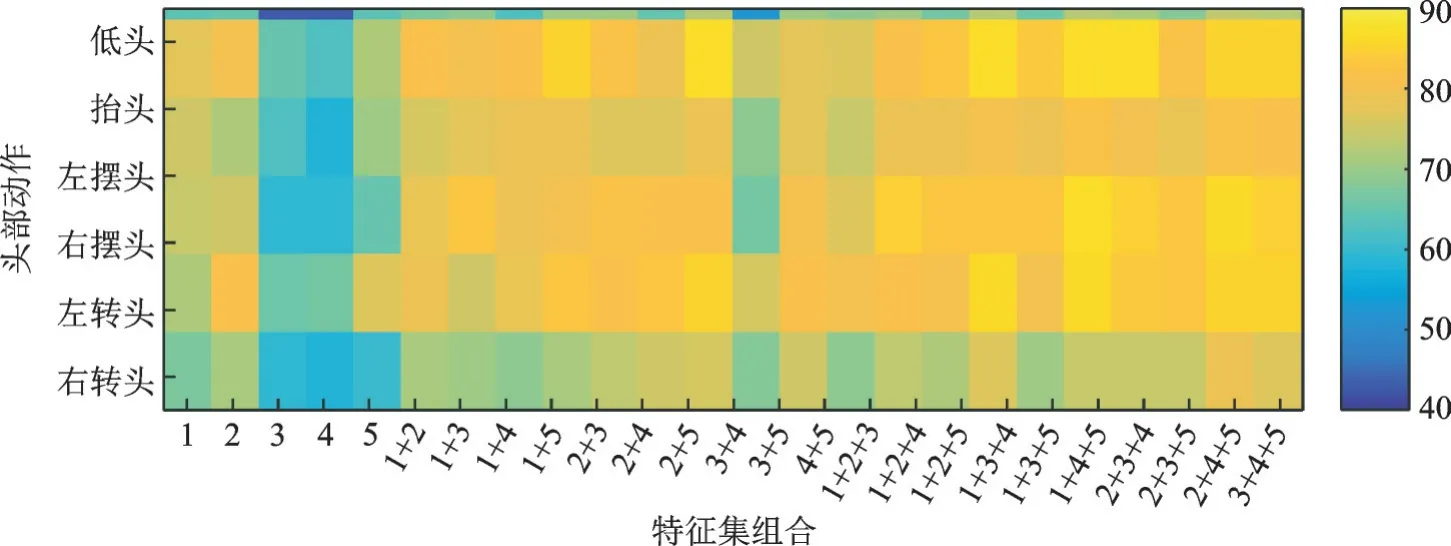
图2 使用KNN 的交叉验证分类精度色块图Fig.2 Color block diagram of cross validation classification when using KNN

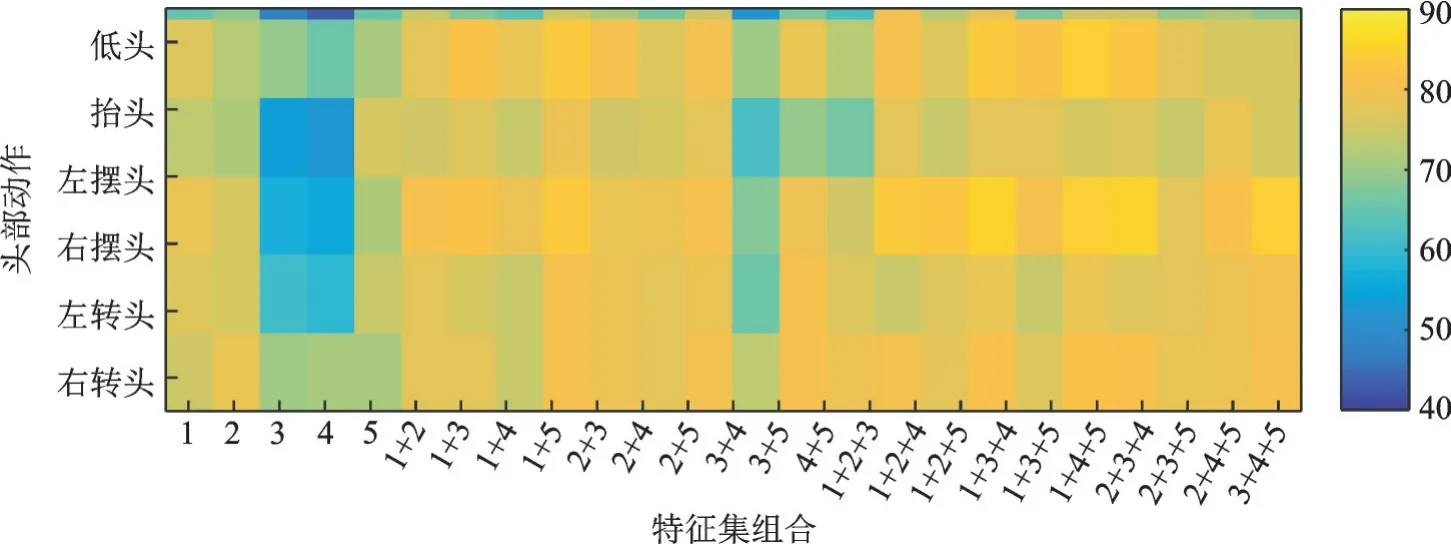
图3 使用LDA 作为分类器的交叉验证分类精度色块图Fig.3 Color block diagram of cross validation classification when using LDA

单独使用一组特征集获得的分类精度体现出一定的差异，在本实验中使用特征集1，2 或5，获得的分类精度高于使用特征集3 或4，表明单独使用时域特征集或非线性动力学特征集的效果可能优于单独使用时-频域特征集。从分别单独使用3 种分类器获得的结果来看，无论使用哪一种分类器，每类动作的识别率均不能达到80%，故单独使用一个特征集并未获得较好的分类效果。

根据使用两组特征集的结果，每类动作的分类精度均明显高于单独使用一组特征集。然而选用不同的两组特征集获得的结果差别明显，例如选用特征集2+5 获得的分类精度相对较好，选用特征集3+4 获得的分类精度最低，表明使用时域特征与非线性动力学特征结合的方式效果较好，仅仅使用同样特征数量的时-频域特征集可能效果相对较差。此时，使用不同的分类器获得的分类精度也体现出一定的差异。

从使用3 组特征集的分类精度看来，其效果相比于使用两组的特征集更好，且使用时域特征+时-频域特征+非线性动力学特征，例如特征集1+3+5，特征集2+3+5 或特征集2+4+5，效果较好。

使用3 种不同的分类器最终获得的结果差别亦较大，使用SVM 获得的分类效果相比于使用KNN或LDA 更好，例如选用特征集2+3+5 时，使用KNN 和SVM 作为分类器识别率分类为81.6% 和86.3%，相差5.1%，如图4 所示。另一方面，选用不同的特征集对于分类结果的影响也较为明显，在选用特征集1+3+5，2+3+5 或2+4+5 时，相比于使用其他特征集组合更好，例如选用特征集1+3+4，特征集2+3+5，使用SVM 作为分类器识别率分别为79.6%和86.3%，相差6.7%。说明采用时域、时-频域和非线性动力学特征混合具有优势。选用上述特征集组合，使用SVM 分类获得的6 类头部动作的识别率均达到80%以上，而此时使用KNN 或LDA 则最终结果有可能低于80%。

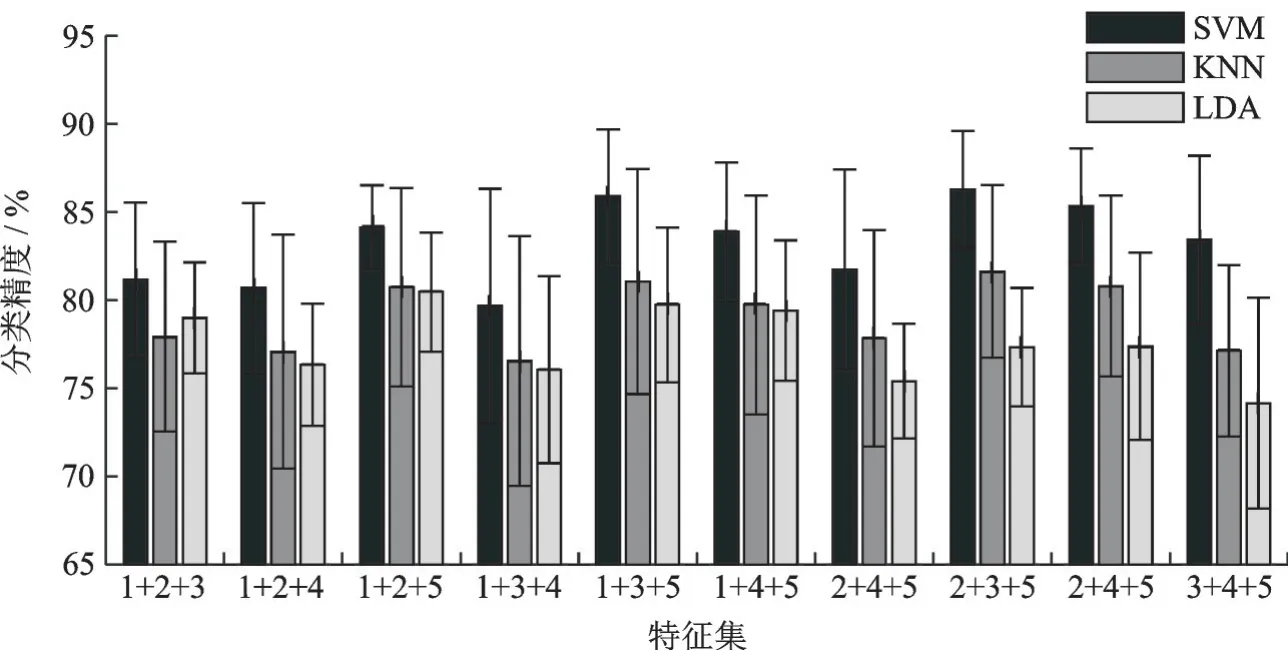
图4 使用3 组特征集组合的平均分类精度Fig.4 Average classfication accracy by using the combination of three feature sets

5 结束语

在本文中，在选用3 组特征集的基础上，分别使用3 种分类器实现了对6 类头部动作的模式识别。实验结果显示：从选用特征集方面而言，使用时域特征+时-频域特征+非线性动力学特征获得分类精度更高；从使用分类器的方面而言，当选用1 组特征集时使用3 种分类器的效果差异不大，然而当选用3组特征集时使用SVM 获得的最终结果相比于使用KNN 或LDA 更好。基于MMG 的假手研究等领域已取得一定成果，而基于头部多类运动的MMG 分类研究则有待于为将来的实际应用做更为深入的研究。根据对头部动作识别的结果，实现对于一些设备的控制，例如开关电视机及切换频道，开关空调及调节温度，甚至是辅助控制电动轮椅，从而可改善一些肢体运动受到限制的特殊残疾人群的生活。