基于第四统计的房颤与正常窦性心律区分方法研究

王星月，陈兆学

（上海理工大学医疗器械与食品学院，上海，200093）

引 言

心房颤动(Atrial fibrillation，AF)即房颤是因心房产生不协调激动而引起的无效收缩[1]，是临床最常见的心律失常之一[2]。AF 的发病率可随年龄增加而明显增加[3]。随着社会老龄化，在未来50 年AF 患病率将增加2.5 倍[4]，并且女性患AF 的症状较男性更为严重[5]。AF 亦可增加中风、心率衰竭等并发症[6]，术后更会带来如炎症、氧化应激[7]等诸多并发症，并且复发率极高[8]，严重危害患者的日常生活与身体健康，因此准确快速地检测出AF，对患者的早期干预以及预后改善至关重要。

由于心电信号(Electrocardiogram signal，ECG)是混沌信号[9]，因此其最突出的特征在R-R 间期也具有混沌特性。在AF 的研究中，利用R-R 间期的混沌性质研究出的Lorenz 图、相空间重构法和概率密度函数(Probability density function，PDF)等方法[10-13]得到越来越多学者的关注，但这些方法往往是从图形变化作为心率变异性最直观的反映。另外随着深度学习的广泛研究，基于AF 在R-R 间期的深度学习检测算法也逐渐被提出[14-16]，但由于算法复杂度很高，需要庞大的数据库支持，因此可行性还有待进一步确证。20 世纪70 年代金日光教授独立地提出第四统计力学[17]，并将之描述为JRG 群子理论[18]，随后利用JRG 群子理论成功地解释了中药学中有关阴阳、归经等理论的内在规律[18-19]。阴阳、矛盾等对立统一规律在自然界中普遍存在，对人体器官之功能而言亦如此，暗含阴与阳相关因素的作用与协同。ECG 的R-R 间期数据是心脏自发搏动产生的相对最稳定和最具代表性的数据之一，能够反映心脏的功能与在位状态，其中必定隐含影响和控制心脏跳动的积极、消极两种因素协同作用的信息。正常窦性心律（Normal sinus rhythm, NSR）和AF 所对应的心脏功能状态有所不同，体现在ECG 数据所得到的R-R 间期上，因对立统一因素具体状态有差异，所对应的第四统计力学特性必然会有所不同。

因此本文研究了第四统计力学的量化方法，结合混沌学分析与第四统计力学阴阳特性表达，对心脏数据R-R 间期进行区分，提出基于第四统计的AF 和NSR 心电信号的区分方法。

1 基本原理

1.1 相空间重构

相空间重构是混沌学分析的首要步骤。根据Takens[20]的相空间嵌入原理：系统中任意分量的演化都是由与之相互作用的分量共同决定的，通过考察某一分量便可重构出系统的相空间，恢复整个系统的运动规律，且保持系统动力学不变。在心脏这一多变量系统中，心电信号R-R 间期时间序列是其中的一个可观察量，本文通过考察AF 和NSR 的R-R 间期时间序列便可重构出对应的心脏系统相空间。

设ECG R-R 间期的时间序列y={yi|i=1,2,…,n}，n为R-R 间期时间序列长度，若要重构m维的相空间Y，则

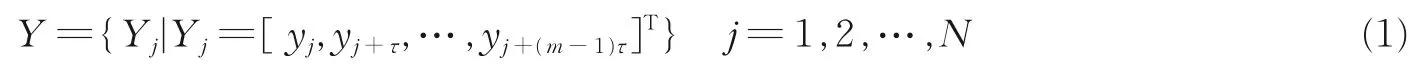
由此得出m维相空间中点的个数为N=n-(m-1)τ。其中m和τ分别表示重构相空间的维数和延迟时间，并且τ可反映信息关联程度，理论上m和τ的取值可分别取[1，n]和[1，n-1]的正整数，但在实际使用中为避免引入过多噪声和冗余量，一般取相对较小但又能充分展开混沌吸引子的值。

1.2 概率密度函数

PDF 是在重构出相空间的基础上研究任意矢量之间的关联程度所提出的重要方法，其基本原理是先构造关联积分C(r)，描述相空间中任意两个矢量Yi和Yj的欧几里得距离d小于领域半径r的概率，即

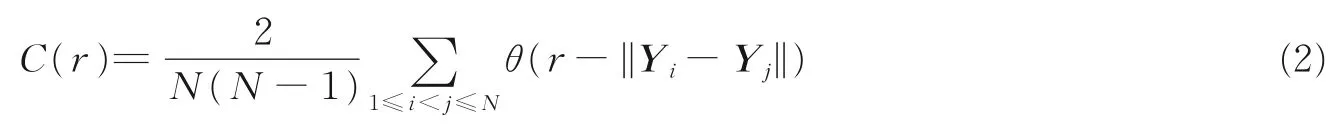
由式(2)可以看出C(r)∈[0,1]，俨然是一个分布函数，其中||*||表示欧几里德距离d，θ(*)是Heaviside 单位阶跃函数，即

再由关联积分C(r)构造概率密度函数P(r)，即

式中：P(r)的计算结果与r的取值有关。因此通过计算AF 和NSR 的PDF 图可以得出相空间中矢量的信息关联程度。

1.3 第四统计力学

第四统计力学的核心是金日光提出的群子理论-JRG 群子理论，该理论界定了生命动力元素群的定量方法：在对立统一的系统中有着许多方向各异、数量不等的正负或阴阳因素影响着系统的发展，而这些因素的综合影响就可描述为各种无规则运动形成的“群子”。人体正是阴与阳的矛盾体，心脏系统是人体矛盾体的重要器官，同样有着或阴或阳的状态特性，因此ECG 的R-R 间期数据可以看作阴阳无规则运动“群子”数据，可以用群子理论进行描述。

JRG 群子理论的量化方法是对某系统某一参量的强度ξ与其分布函数x的归一化数据在特定时空做出直方图，并找出一条最适合的曲线进行拟合，过程中利用3 个群子统计参数k,r1,r2表达曲线分布情况，这3 个参数分别代表阴阳群子静态阴阳比度和内部阴、阳群子的动态竞争能力。最终利用其核心含义JRG 群子理论可表达为一个非常简洁的公式[19]，即

式中：ξmax和ξmin分别表示最大强度和最小强度，x为分布函数，因此x∈(0，1)，并且k=阴/阳。在 JRG 群子理论中根据r1,r2的取值可得出ξ-x呈现5 种单调递增的关系，如图1 所示。

图 1 5 种 ξ-x 单调递增关系Fig.1 Five kinds of monotone increasing relations of ξ-x

当r1=r2时，阴阳效应群子聚集的倾向性相同，阴阳竞争能力均等(图1(a))；当r1→0，r2→0 时，阴阳效应群子聚集的倾向性是高度的均一分布(图1(b))；当r1＞1，r2＞ 1 时，阴阳效应群子聚集的倾向性是复杂的双峰分布(图1(c))；当r1＜ 1，r2＜ 1 时，r1≪r2，阴阳效应群子聚集的倾向性阴＜阳，阳性竞争力占优势(图1(d))；当r1＜ 1，r2＜ 1 时，r1≫r2，阴阳效应群子聚集的倾向性阴＞阳，阴性竞争力占优势(图 1(e))。

若已知系统的某一参量的强度ξ和其分布函数x，采用多元非线性回归法，可求解出三参数，回归模型ξ-x为

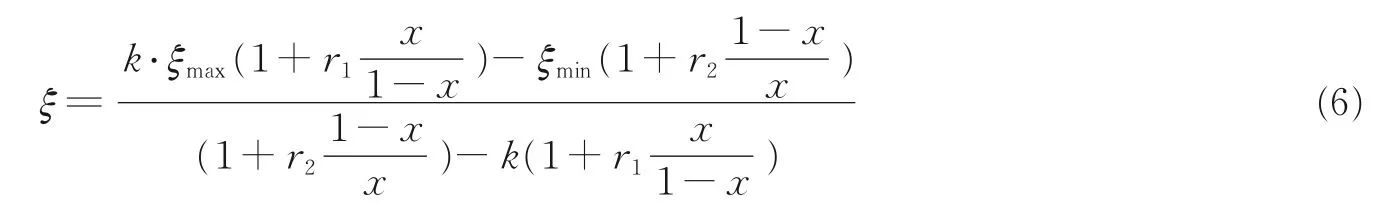
求解过程可分为两次，取第1 次拟合后x=0.5 所对应的ξ0.5，令r1=r2=1，即可根据式(7)求出k，从求解过程看出k值的结果可反映拟合曲线的平均高度；第2 次求解时再将k作为真实值再次代入式(6)所表示的回归模型，即可回归出r1和r2。

由式(7)可知k的初值选取一般以曲线的平均高度相关，平均高度越低，k值越小；r1，r2则代表曲线横向、纵向能够拟合的程度，曲线所在坐标越低，初值选取应当越小，因此回归时可根据实际情况选择拟合初值。其中k值可表示为心脏系统的阴阳宏观变动，r1，r2可看作心脏系统阴阳群子内部的变动，其结果往往是微小的。

2 本文算法

为从心脏系统整体上进行阴阳因素的解析，本文结合混沌性质与阴阳特性，对AF 和NSR 的R-R间期数据进行分析，首先要确定混沌系统的嵌入维数m。

2.1 嵌入维度选取

为保证单因素控制变量，首先需要对嵌入维m进行选取，若τ不变，m逐渐增大，系统将达到某一饱和状态。为选择一个统一的相对小的m，本文作出某一延时τ下AF 和NSR 的R-R 间期随嵌入维度m=2，3，4，5，6，8，15，20，30 的 PDF 变化图，AF 和 NSR 的变化情况相似。随机选取一个变化情况如图 2 所示，从图中可看出，在某一延时τ下，当m较小时，PDF 图不能很好地拟合，这是由于R-R 间期混沌吸引子没有完全展开；而随着m的增加，曲线向右移，相空间中的混沌吸引子逐渐展开；当m≥6 以后混沌吸引子已基本展开达到饱和。由于过大的m只会产生冗余的数据量，增加计算复杂度，因此本文取m=6，既可恢复AF 和NSR 所有数据原本的动力系统，又可避免增加过多的混沌吸引子的几何不变量。

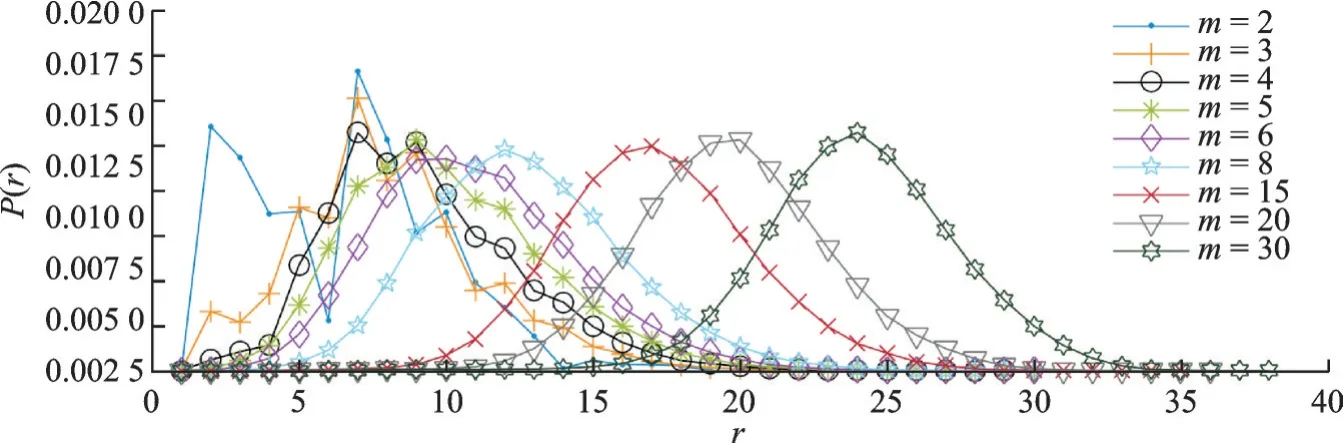
图2 在不同m 条件下P(r)随r 的变化曲线Fig.2 Curves of P(r)with r at different m

2.2 本文算法流程

确定好统一的嵌入维m=6，将 AF 和 NSR 的 R-R 间期数据按式(1)构建 6 维相空间，延时τ从 1 开始逐一增加至30；接着按照式(4)逐一绘制PDF 图，将每一个PDF 图看作心脏R-R 间期数据在特定时空下的ξ与x归一化直方图，将领域半径r作为强度ξ，每个领域半径对应的P(r)作累加和作为分布函数x，实现由矢量关联程度到阴阳状态的转换，即

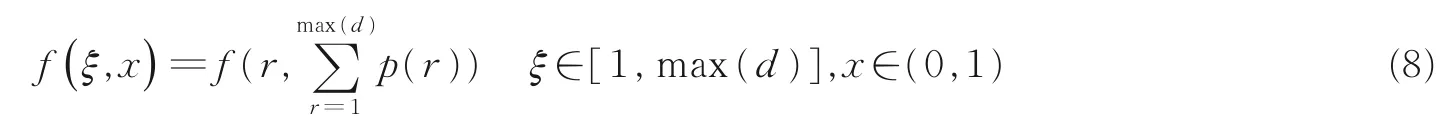
从而得到ξ与x的对应关系，代入式(7)计算出k值，τ逐一增加，便可得到k值与随τ的变化。

由此，R-R 间期图形学的信息关联程度变化将表示为数值型的k值的变化，以k的变化来分析AF 和NSR 心脏系统的阴阳状态。最后还提出以k值的微分累加和作为区分AF 和NSR 的重要参数。本文算法流程如图3 所示。

图3 本文算法流程图Fig.3 Flow chart of the proposed algorithm

3 数值计算与分析

3.1 数据与预处理

本文采用国际公认的PhysioBank 心电数据库中的长时AF 数据[21]和长时NSR 数据[22]，采集频率均为128 Hz。由于数据是在24 h 长时采集的，涉及睡眠与运动状态，会因大幅度的震动(如打喷嚏、翻身)等原因导致数据出现空缺，因此需要进行预处理。正常人安静时心率为60～100 次/min，睡眠时降低，运动时加快，因此可认为NSR 的R-R 间期在500～1 200 ms 之间；而AF 患者的R-R 间期由于病理性原因数据本身波动性较大，应当放宽预处理范围，因此剔除[200，2 000]ms 之外的数据。图4，5 分别为随机选取500 个R-R 间期NSR 和AF 数据点后得到的预处理前后结果。

图4 NSR 数据预处理前后结果Fig.4 NSR data before and after preprocessing

图5 AF 数据预处理前后结果Fig.5 AF data before and after preprocessing

经过如上预处理后，从NSR 和AF 数据中划分出1 800 个数据段(AF900 段，NSR900 段)，每个数据段包含2 000 个R-R 间期数据点，其中2/3 数据段用于计算，1/3 数据段用于对比验证。实验在MATLAB R2016b，在Windows 10 环境下进行编程计算。

3.2 概率密度函数图

PDF 的计算按照式(4)，本文取r∈[1，max(d)]，囊括所有的概率，绘出 AF 和 NSR 数据段的P(r)随r的变化图，分别选取一个 R-R 间期样本(分别为 nsr001、data01)随 τ =1，2，3，10，20，30 的 PDF 变化，结果如图6 所示。为方便显示，横轴r每隔10 个数据点取一个值。图6(a)中NSR 的PDF 曲线随延时τ的增大向右移动，逐渐趋于正态分布；图6(b)AF 的PDF 图中，PDF 值基本不随延时τ发生变化，始终接近正态分布，由此可看出，基于同样大小的相空间，NSR 的R-R 间期关联性会随延时τ的增大而逐渐变弱；而AF 的R-R 间期关联性本身就比较弱，不随τ发生明显改变。

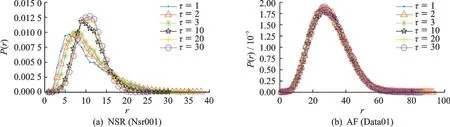
图 6 P(r)随 τ 的变化曲线Fig.6 Curves of P(r)with τ

3.3 第四统计力学参数求解

基于第四统计力学原理对AF 和NSR 的PDF 图的信息关联程度变化进行定量分析，将图6(a, b)中τ为 1 的r-p(r)曲线图按式(8)转化为ξ-x关系图，即为图 7(a, b)中的“拟合前”数据。

从图7 可看出，AF 和NSR 的第四统计ξ-x曲线高度都较低，属于图1（d）分布。经过反复实验并结合图 1（d）分布的 3 参数的意义，设定 AF 和 NSR 的初始化参数k,r1,r2为[0.5，0.000 1，0.01]，经过式(6)所示的回归模型得到图 7 中ξ-x的“拟合后”曲线。当τ=1 时，NSR 数据拟合得到ξ0.5=68.8，由式(7)计算得出k=0.206，同理 AF 的ξ0.5=256.3，k=0.235。将τ逐渐增加到 30，可得出 NSR 和 AF 的每一个τ值对应的k值变化。本文选取随机的10 个NSR 和AF 的R-R 间期数据段显示k值随τ的波动情况，如图8所示。

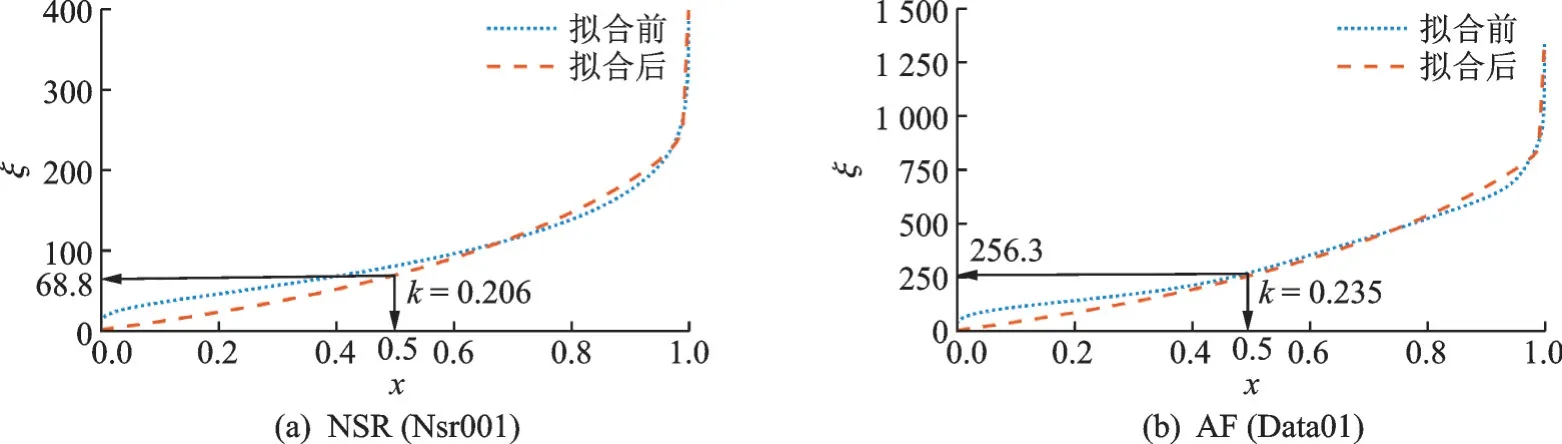
图7 图6 中τ=1 条件下的第四统计拟合结果Fig.7 The fourth statistical fitting results under the condition of τ=1 in Fig.6

图8 中，基于相同大小的相空间以及初始值，当延时τ较小时，NSR 的k值都从0.2 左右逐渐增大且分布于某一固定值以下（图8(a)）；而图8(b)中AF 的k值分布则是呈现大小不定而后基于某一均值上下波动的状态，可证明NSR 的系统较AF 比较同一，且阴阳配比状态相对稳定。当延时τ逐渐增大，AF 的k值始终呈现较为平稳的波动，而NSR 的k值随τ的增大呈现缓慢上升而后平稳波动的变化趋势，反映出NSR 的系统内部阴、阳双方力量对比随τ的增加而逐渐显得随机，即关联性随着τ的增加而变弱，同时也说明AF 的阴、阳力量对比始终是偏于随机的，即关联性本身就非常弱，这与PDF 图反映的关联性结果一致。

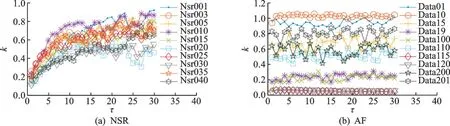
图 8 k 值随 τ 的变化结果Fig.8 k value fluctuates with τ

4 结果分析与对比验证

4.1 微分累加和

为了从量化角度来更加明确地区分AF 和NSR，不仅要描述k值缓慢上升或始终平缓的变化情况，还要避免当τ逐渐增大使得k值上下波动导致的误差，因此本文引入微分累加和的数学计算方法，令微分累加和为Ksd，即

式中diff 是后项与前项的微分。计算出NSR 和AF 各600 段R-R 间期数据段的Ksd 值，结果如表1 所示。NSR 的Ksd 值都大于0.3 且小于1，而AF 的Ksd 值的样本结果都小于0.3，有的甚至小于0，并且从段数分布可以看出AF 的Ksd 值大部分小于0.2，因此可将Ksd=0.3 作为界限用于区分NSR 和AF。

表1 Ksd 值在各区间的段数分布Table 1 Number distribution of Ksd value in each interval

4.2 检验与对比

为使实验更加严谨，将同样长度的AF 和NSR 各300 个数据段用于验证，结果如混淆矩阵表2 所示，其中TP和TN分别代表真阳性和真阴性的数目，FP和FN分别代表假阳性和假阴性的数目。表2的检验结果所示对于AF 的检出具有比较好的效果。本文还通过混淆矩阵构造如式(10)所示的3 个指标，分别代表准确率、敏感性和特异性，作为本文算法与典型的支持向量机（Support vector machine,SVM）分类算法的对比评价指标，如表3 所示。

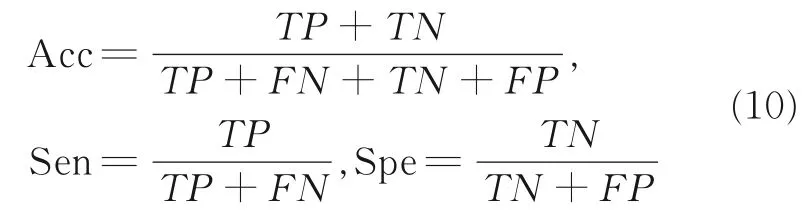
利用LIBSVM 这种SVM 分类工具包，提取同样长度的AF 和NSR 各300 个数据段的5 个特征，数据段的均值与方差；相邻R-R 间期的差分均值、差分均方根以及差值大于50 ms 的数量，并将所有特征归一化至[-1，1]之间，组成特征向量输入，利用网格搜索法寻找最佳参数c(惩罚因子)和g(径向基核函数的参数)，得出训练集准确率为96.92%，测试集准确率为90.67%。Acc，Sen 和Spe 越高，算法的效果越好。本文方法的3 个指标都比SVM 好，从另一方面验证了本研究的可行性及优势，本文方法的准确率为97.83%，并且敏感性较高，检出AF 都小于0.3。

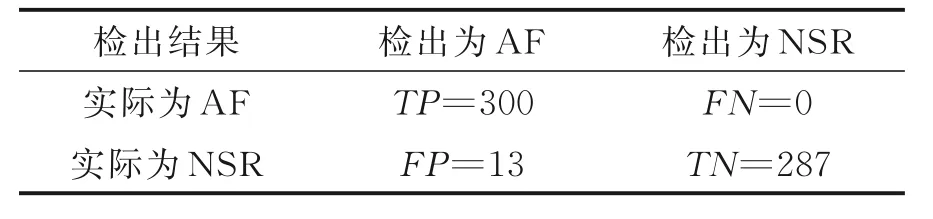
表2 本算法的检验结果Table 2 Test results of the proposed algorithm

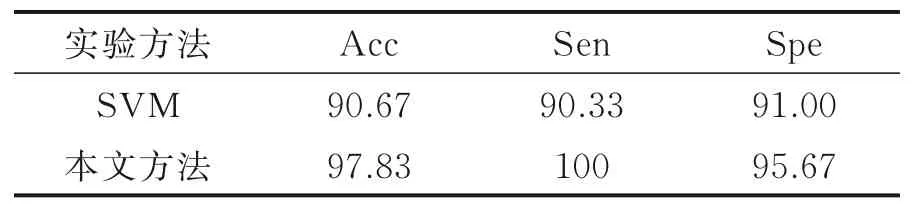
表3 二分类指标对比Table 3 Comparison of two classification indexes%

5 结束语

本文研究了以第四统计力学的阴阳特性区分AF 和NSR 的方法，不仅通过PDF 图证明AF 和NSR的R-R 间期的关联性随τ的变化，即AF 关联性较NSR 弱；而且利用PDF 的分布数据拟合出对应的R-R间期的群子参数k值以及k值随τ的变化，即NSR 的k值变化初始时较AF 相对同一稳定，而后逐渐呈现随机状态，而AF 始终偏向随机。本文还提出以k的微分累加和Ksd=0.3 作为区分AF 和NSR 的重要参数，在对比检验的中也看出本文方法是可行的。

本研究不仅在第四统计力学的应用领域打开了新途径，将阴阳特性表达用于心脏数据R-R 间期的区分，也对未来心血管疾病的研究具有重要意义，尤其有可能作为中西医结合相关的方法学和基本技术，为与中医相关的临床理论与实践研究提供启发。但是由于AF 数据本身波动性较大，长时性采集数据易产生许多奇异点，且第四统计力学对直方图边界值具有较强的敏感性，也会影响检测的准确性，因此本文的数据段均选择平稳且具有代表性的数据段。另外本文还未对不同数据长短以及延迟时间取值范围等方面进行讨论，未来可作进一步研究和改进，并将第四统计应用于更多的心电数据。