开方形孔对形状记忆合金板力学性能影响研究
2020-08-11段文峰刘文渊
孔 境,段文峰*,刘文渊
1吉林建筑大学 土木工程学院,长春 130118 2南京理工大学 泰州科技学院,江苏 泰州 225300
形状记忆合金(Shape memory alloy,英文缩写为SMA)是一种智能材料,具有特殊性能,在经历大变形后能恢复到未变形前的形状.由于SMA材料的超弹性、形状记忆效应等性能,在航空、医学和工业等领域得以广泛应用[1-2].大多数应用中常采用SMA线材形式.为了更好地将SMA材料应用到工程领域、实现合金材料在形状及加载条件更复杂情况下的应用,出现了对SMA板材的一系列试验研究.
NiTi基的形状记忆合金具有相对较大的变形性能,是常用的SMA材料[3].Shariat等[4-5]人讨论了孔的数量、方形孔及圆孔的参数对NiTi合金板件应力-应变曲线的影响,研究表明,NiTi薄板开孔后,马氏体正相变曲线出现降低的现象,并且随着开孔个数及孔径的增加,曲线降低性能越来越明显.随后Zhu等[6-7]人建立了开不同阵列圆孔的SMA板件的有限元模型,通过对模型的观察发现,孔周围存在应力集中现象,且孔隙之间存在着复杂的非线性关系.张芸等[8]人研究了几何缺陷对厚度为1 mm的Ti 7.5 Nb 4 Mo 2.5 Sn合金薄板的材料性能的影响,结果表明,带中心圆孔与单边半圆缺口的试件,缺口处出现了应力集中现象,降低了材料的塑性及超弹性性能.随后王宏等[9]人通过对0.7 mm厚的Ti 7.5 Nb 4 Mo 2.5 Sn开孔合金薄板的拉伸曲线的观察发现,随着圆孔直径的增加,SMA薄板的屈服强度及伸长率逐渐减小,材料的超弹性性能逐渐变差,而当增大孔的中心距时,材料的伸长率则不会发生变化.上述研究仅涉及圆孔方面,对方形孔方面的研究涉及较少,因此本文拟对开长方形孔的板材的受拉性能开展研究,采用ANSYS有限元软件,建立NiTi基SMA板件的实体数值模型,以研究方形孔开孔长度对SMA板受拉性能的影响.
1 有限元模型验证

图1 SMA的应力-应变曲线Fig.1 Stress-strain curve of SMA
SMA材料具有可恢复变形能力,其典型的应力-应变曲线如图1所示,σMS与εMS分别为马氏体相变开始时的应力和与应变,σMf与εMf分别为马氏体相变结束时的应力和应变,σAS与εAS分别为奥氏体相变开始时的应力和应变,σAf与εAf分别为奥氏体相变结束时的应力和应变.
目前,文献[5]已完成了Ni-Ti基形状记忆合金板的试验研究,试验证实了SMA板件具有自复位能力,试验温度条件为303 K,材料性能参数见表1.板件为长方形板,板的厚度t为0.1 mm,长边L为30 mm,短边H为4 mm.

表1 材料性能参数Table 1 Material performance parameters
本文对文献[5]中试验进行有限元模拟,SMA板件在拉力作用下的Mises应力分布情况及曲线如图2~图3所示.

图2 SMA板件的应力云图Fig.2 Stress nephogram of SMA plate

图3 应力-应变曲线Fig.3 Stress-strain curve
图2给出了SMA板件拉伸变形达长度L的6 %时的Mises应力分布.由图2可以看出,当板件进行拉伸时,试件中部应力分布均匀,而板件存在应力集中现象,Mises应力呈上下、左右对称分布.图3给出了数值模拟曲线与试验曲线的对比情况,由图3的应力-应变曲线可以看出,SMA板件加载开始时曲线斜率较大,当到达屈服强度时,随着应变的增加,曲线趋于水平,应力不再发生明显变化,变形达到6 %时卸载,卸载曲线与加载曲线近似平行,直至应力降至为0.数值模拟发现Ni-Ti基SMA板具有良好的复位变形能力,且模拟曲线与试验曲线吻合较好,可见数值模型可有效地进行Ni-Ti基SMA板拉伸试验模拟.
2 数值模拟
2.1 模型建立
采用ANSYS有限元软件建立SMA板件的有限元模型,试件材料采用上文模拟验证文献[5]中的NiTi合金板.模型采用Solid 185单元,单元由8个节点定义,每个节点具有3个自由度,该单元可以模拟超弹性、大应变及大变形能力.为了保证形状的规则,网格划分器选择的是映射网格划分,便于形状和尺寸的控制.左侧板件约束3个方向自由度,右侧约束UY,UZ 2个方向的自由度,加载时对右侧施加UX方向的位移荷载,位移荷载分别为加载至试件加载边长度L的2 %,4 %和6 %变形后卸载.
2.2 试件设计
试件开孔图如图4所示,试件的长度为L,试件的宽度为H,试件中部开矩形孔长度为a、宽度为b.试件设计时保持孔宽度b不变,改变孔长度a设计试件S 1~S 4,试件具体参数如表2所示.

图4 板件开孔示意图Fig.4 Schematic diagram of plate opening

表2 试件参数Table 2 Specimen parameters
2.3 模型分析
图5为变形达到长边L的6 %情况下a分别取b,2b,3b和4b时开孔板件的Mises应力情况,板件编号分别为S 1~S 4.与图2对比发现,板件开孔后,试件的Mises应力显著增大且集中于开孔处,最大应力增加约1倍.
由图5可见,开孔板件的应力分布同样呈上下、左右对称分布;开孔板发生较大变形时,应力主要集中在开孔的附近,且开孔上下区域部分的应力,远大于其它区域,应力集中分布区域与加载方向平行,而垂直加载方向的开孔区域附近应力变化情况较小;随着开孔尺寸a的增加,图5(a)~图5(d)中S 1 ~ S 4板件的Mises应力先发生了微小增加,随后逐渐降低.
随开孔距离a的增加,集中力逐渐向方形孔上下边的中间扩展,出现应力分布从两侧向中间逐渐增大的现象;板件中开孔长度超过3b后,除了开孔位置、固定端及加载端附近存在应力集中外,试件中间部位的应力分布趋于均匀.

(a) S 1板件应力云图(a) Stress nephogram of plate S 1

(b) S 2板件应力云图(b) Stress nephogram of plate S 2

(c) S 3板件应力云图(c) Stress nephogram of plate S 3

(d) S 4板件应力云图(d) Stress nephogram of plate S 4
图6给出了S 1~S 4开孔试件的应力-应变曲线.由图6可以看出,SMA板开孔后,变形在2 %以内时,曲线发生了明显的变化.与不开孔板件相比,加载时开孔后板件的马氏体相变应力下降与文献[4-5]的结论相同,在曲线中表现为奥氏体阶段出现了折线上升的现象,且随着开孔长度的增加相变应力呈先下降然后保持稳定(并出现平台段);卸载时板件奥氏体相变结束应力也出现了明显的降低现象,且随着开孔长度的增加相变应力呈先下降然后保持稳定(并出现平台段).曲线发生变化时的范围也较开圆孔时的较小.板件变形在2 %~6 %范围内,应力-应变曲线无明显变化.SMA板件开孔后仍具有可恢复变形能力,且无残余变形产生.
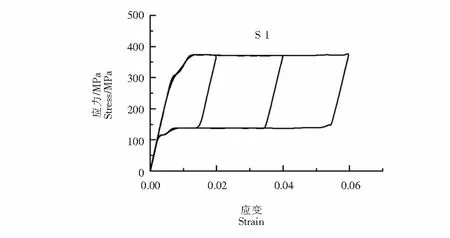
(a) S 1曲线(a) S 1 curve

(b) S 2曲线(b) S 2 curve

(c) S 3曲线(c) S 3 curve

(d) S 4曲线(d) S 4 curve
3 结论
本文通过ANSYS有限元分析软件,建立SMA板材的实体模型,对开方形孔的形状记忆合金板抗拉性能进行了参数分析,得出如下结论:
(1) 通过采用实体单元对SMA板件拉伸试验进行数值分析,发现模拟结果与试验结果吻合较好.
(2) SMA板件开方形孔后试件出现应力集中现象,最大Mises应力较未开孔板增加约1倍.
(3) 开方孔的SMA板件在开孔处出现了应力集中现象,应力集中方向平行于加载方向,应力从开孔处的中间向两边降低,随着开孔长度的增加应力集中有所缓解.
(4) 板件开方形孔对SMA材料的应力-应变曲线产生影响,影响范围在2 %变形位置内,应力集中使加载时板件的平均相变应力降低,曲线出现了折线形增长,卸载时板件的平均逆相变应力也出现了较大的降低.
(5) 板件开方形孔虽然会降低材料的部分力学性能,但板件仍具有复位变形能力,且无残余变形的产生.
