渗透数学思想，提升核心素养

李冬华

摘 要：数学基本思想是“四基”之一，然而在实际教学中，经常可以看到一些教师忽略了数学基本思想的渗透，这样会影响学生数学核心素养的提升。教师在教学过程中要结合教学内容恰当地渗透数学思想。低年级学生以形象思维为主，数形结合有利于学生理解知识，厘清知识的来龙去脉。转化思想可以贯穿于整个小学阶段的图形教学中。而建立数学模型，有利于知识的归纳整理和思维能力的提升。

关键词：渗透;数学思想;核心素养

《义务教育数学课程标准（2011年版）》在课程总目标中提到“四基”即：基本知识、基本技能、基本思想、基本活动经验。基本思想就是“四基”之一，可见数学基本思想是多么重要。在实际的教学中，经常可以看见一些教师为了应试只注重基本知识和基本技能的教学，忽略了数学基本思想的渗透。这样相当于忽略了数学的本质，对学生的数学核心素养的提升将会有很大的影响。在教学中如何渗透数学基本思想呢？现谈谈我的一些做法。

一、数形结合思想

低年级学生活泼、好动，以形象思维为主，因此在低年级的课堂教学渗透数学结合的思想，不仅能提高学生的思维能力，而且能更好地帮助学生理解知识，厘清知识的来龙去脉。如教学人教版二年级上册中的“进位加法笔算”。

（一）延续情境，提出问题

1.呈现主题图和上一节课同学们提出的问题：二（1）班和二（3）班一共有多少名学生？

2.提问：解决这个问题，需要知道什么信息？（二1班35人，二3班37人）

3.提问：怎样列式？

板书： 35+37=？

（二）数形结合，理解算理

1.想一想，摆一摆

提问：你想用什么办法算出得数？

预设：摆小棒、竖式计算……

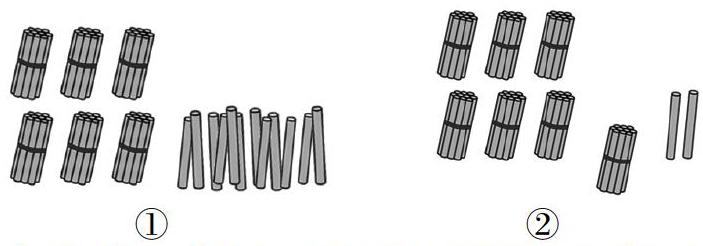
引导学生自主摆小棒，汇报摆法。预设学生的情况有：

……

提问：哪种摆法能让人一眼就能看出结果是72根？说说理由。

小结：第②摆法，满十根捆成一捆，容易看出一个十。

2.写一写，说一说

提问：你能把摆小棒的过程用竖式记录下来吗？

学生尝试用竖式计算。

【设计意图：把数与形连通起来，通过数形结合，帮助学生理解算理。】

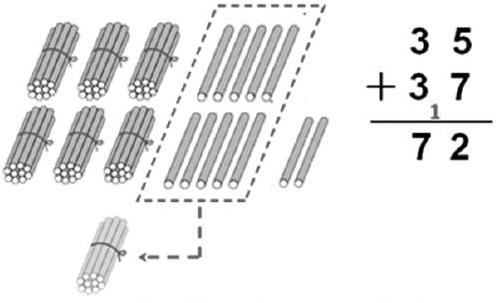
（1）教师引导结合黑板上小棒图理解算理和算法：

①摆的时候整捆的和整捆的对齐，单根的和单根的对齐，在竖式里就是相同数位对齐。

②先把5根和7根合起来，得12根，满10根捆成一捆 ，还剩两根。在竖式中也就是先算个位5加7得12，向十位进一，个位上写2。这个1叫进位1，要写小一点，写在十位的右下角。

③算三捆加三捆加1捆，在竖式中就是再算十位的三加三加进位一得7，在十位上写7。

所以35+37=72

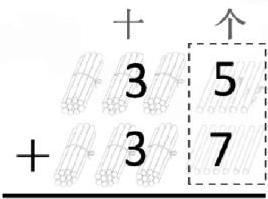
（2）对应课件中的小棒图，请学生说竖式计算过程。

（3）同桌说竖式的计算过程。

【设计意图：结合小棒图有序地呈现“35+37”的豎式计算过程，特别是动态显示突出单根相加满10根，把10根捆成1捆的过程，通过数形结合进一步理解进位的道理。】

二、转化思想

转化思想可以贯穿于整个小学阶段的图形教学中。这一类型的课只要上好第一节的种子课，触类旁通，就知道这一类型的课怎样上了。现就以人教版“平行四边形的面积”为例，谈谈转化思想在教学中的运用。平行四边形的面积是人教版五上“多边形的面积”这一单元的一节起始课，上好平行四边形的面积这节课，后面三角形的面积，梯形的面积以及六年级圆的面积和圆柱的体积，都可以用转化思想，通过把新图形转化成以前学过的图形，从而推导出计算公式。

教学片段：

1.用数方格的方法计算面积

师：同学们想一想我们可以怎样知道这两个花坛的面积？学生回忆。（数方格、用公式计算）

师：请同学们打开数学书P80，请大家数一数画在方格纸上的两个花坛的面积，并填写表格。

（1）学生填表。

（2）指名汇报填表情况。

（3）观察表中数据，你发现了什么？

生：我发现长方形的面积=长×宽，平行四边形的面积=底×高。

（4）猜想：是不是所有的平行四边形的面积都可以用底×高这个方法计算面积呢？你有什么办法证明？

2.动手操作，验证猜想

（1）动手操作，转化图形。

请小组长拿出信封中的学具（平行四边形，剪刀），四人小组一起研究。

（2）汇报交流。

请一小组在实物投影上演示并汇报。

生1：把平行四边形沿着高剪开，得到一个三角形，把这个三角形平移后拼在另一边，得到一个长方形。

生2：我们发现长方形的面积和平行四边形的面积相等。

生3：我发现长方形的长与平行四边形的底相等，这个长方形的宽与平行四边形的高相等，

因为长方形的面积=长×宽，

所以平行四边的面积=底×高

（3）教师再用课件展示转化过程。

板书：平行四边形的面积=底×高，

S=ab

（4）全体学生闭上眼睛，边回忆边说转化过程。

（5）教师小结：

正像同学们所发现的，我们把一个平行四边形转化成为一个学过的长方形，它的面积与原来的平行四边形面积相等。这个长方形的长与平行四边形的底相等，这个长方形的宽与平行四边形的高相等，因为长方形的面积=长×宽，所以平行四边形的面积=底×高。我们通过剪—平移—拼的方法，把平行四边形转化成我们学过的长方形，这种转化的思想在今后的学习中还会大量用到。

三、模型思想

《义务教育数学课程标准（2011年版）》指出：在数学课程中，应当注重发展学生的推理能力和模型思想，模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。建立和求解模型的过程包括：从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果并讨论结果的意义。这些内容的学习有助于学生初步形成模型思想。

如教学人教版六年级上册的“工程问题”。

教学片段：

（一）阅读与理解

1.出示情境图

这条道路，如果我们一队单独修，10天能修完。如果我们二队单独修，18天才能修完。如果两队合修，多少天能修完？

师：你知道哪些信息？求什么问题？

2.质疑

师：读完题后，有什么疑问吗？

生：题目没有告诉总长，不能求出问题。

师：有什么办法解决？

生：假设总长。

师：你想假设道路的总长是多少？（30米，60米，90米……），为什么选这些数？

（二）分析与解答

1.小组学习。请同学们用你们假设的道路总长度解决问题。

2.小组汇报：

组1：假设道路总长30米。

30÷（30÷10+30÷15）

=30÷5

=6（天）

组2：假设道路总长60米。

60÷（60÷10+60÷15）

=60÷10

=6（天）

组3：假设道路总长90米。

90÷（90÷10+90÷15）

=90÷15

=6（天）

3.学生提出疑问

师：看到各组的解答，有疑问吗？

生：为什么总长不同，而合修的天数都是6？

4.小组学习：画一画，说一说

一队、二队每天修的米数分别占全长的几分之几？两队每天合修的米数又占全长的几分之几？

5.小组汇报

x

组3：如果假设其他长度还是这样吗？你发现了什么？

这时一个学生说，既然这样，我们就可以把道路长度看作单位“1”。把道路的长度假设为1更简便。

（三）巩固练习

2.书上的做一做

（四）对比归纳，建立模型

师：请同学们看，我们今天学习的所有的题目，列式有什么共同点？

生1：都有总量，都用总量除以……

生2：总量可以叫工作总量。

生3：都要求工作效率。

师：什么是工作效率？

生4：我发现这些题目都是用工作总量÷工作效率=工作时间

在学生纷纷发言后，最后总结得出模型：工作总量÷工作效率=工作时间。

总之，还有很多的数学思想，如符号化思想、假设思想、极限思想等，我们在教学中要择时择机加以渗透，以提升学生的数学核心素养。

参考文献：

王永春.小学数学核心素养教学論[M].华东师范大学出版社，2018.

编辑 冯志强