基于蚁群算法的湛徐高速公路中长期养护费用分配分析
2020-08-10刘跃生
刘跃生
(广东能达高等级公路维护有限公司,广东 广州 510030)
公路养护是确保公路长期稳定运营的关键。随着运营车辆的逐日增多,公路病害越来越多,养护频率和养护费用增加。当前公路养护决策者“重建轻养”,道路养护也未形成系统、科学的方法,工程师经验往往影响养护频率及养护效果,很难使养护费用得到高效的养护结果。加上公路养护的定额费用年度分配不合理,不能有效解决公路病害,因而很难进行全路段养护。对公路养护费用进行科学分配,可优化养护费用分配方法,获得最优养护效果,还可通过养护费用分配模式动态了解公路运营状况,方便制定科学的决策计划。国内学者提出了一些费用分配方法,建立了费用分配模型,如基于模糊推理的智能资金分配模型、动态规划法下养护费用单目标优化分配模型、单年度资金优化分配模型、基于α-鲁棒的公路养护费用分配模型、蚁群算法养护模型等。其中蚁群算法可对路面状态进行识别,有针对性地分配养护费用,避免各路段平均分配养护费用等不合理现象。该文针对湛徐(湛江—徐闻)高速公路路面养护,基于蚁群算法构建养护费用分配模型进行中长期养护费用分配。
1 中长期养护费用分配模型及思路
1.1 公路多年度分配模型
路面养护费用并非每年固定不变,需结合路面性能状态进行分配。为合理获得各年度养护费用大小,建立多年度费用分配模型。建模时需考虑以下几点:1) 设定一个养护规划期,可以是5、10年等;2) 设定养护资金及反映路面性能的指标作为约束水平;3) 采用灰色GM(1,1)模型对各年度路面性能指标进行预测;4) 采用蚁群算法结合MATLAB编程求解。
根据以上要求,选择5年中长规划期,基于路面状况,收集多个预测数据,设置路面损坏状况指数PCI及费用两个约束条件进行规划期内各年度养护费用分配,通过蚁群模型反复计算,获得满足约束条件的各年度养护费用分配结果。各年度以PCI为约束条件的费用分配计算式如下:
(1)
其他约束条件:
(2)
(3)
(4)
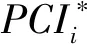
PCI按下式计算:
PCI=100-a×DRb
(5)
式中:a、b为系数;DR为路面综合破损率,DR=D/A×100;A为路面总面积。
对2014—2015年湛徐高速公路路面PCI值与DR的关系进行回归,得到a=15、b=0.412。采用蚁群算法进行关键指标求解,求解过程如下:1) 读入路段数据;2) 将数据初始化;3) 设置信息素浓度;4) 迭代次数加1;5) 进行蚂蚁k=0计算;6) 进行蚂蚁k=k+1计算;7) 随机给定第一个节点参数;8) 选择节点;9) 按照转移概率选择另外一节点;10) 若全部节点操作完毕,进入下一步,否则返回步骤8;11) 求解适应度,更新信息素;12) 若全部蚂蚁操作完毕,则进入下一步,否则返回步骤6;13) 若达到迭代次数,则输出结果,否则返回到步骤4。
1.2 养护费用分配思路
(1) 将养护费用均分为5等份,养护规划年度内各一份,再结合路面病害类型进行养护费用分配。
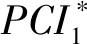
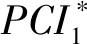


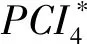
(7) 比较5年规划期内PCI值,若满足设置的PCI值要求,则费用分配结果为最优,否则再次对养护费用进行各年度分配并计算各年度的PCI值,直至其满足约束要求为止。如此反复计算,获得最佳养护费用分配方案。
2 湛徐高速公路中长期养护费用分配
2.1 湛徐高速公路概况
湛徐高速公路为(沈阳)同江至(海南)三亚国道主干线中的粤境路段,主线长114.302 km,2010年正式通车,运营一段时间后出现各种路面病害,相关部门每年均安排养护资金进行路面维护。为分析方便,选择其中一段近几年的检测数据、路面破损状况及修复资金作为其后期养护费用分配的基础数据。湛徐高速公路部分路段近5年路面状况指数见表1,基年路面破损状况见表2。

表1 湛徐高速公路部分路段近5年路面状况指数
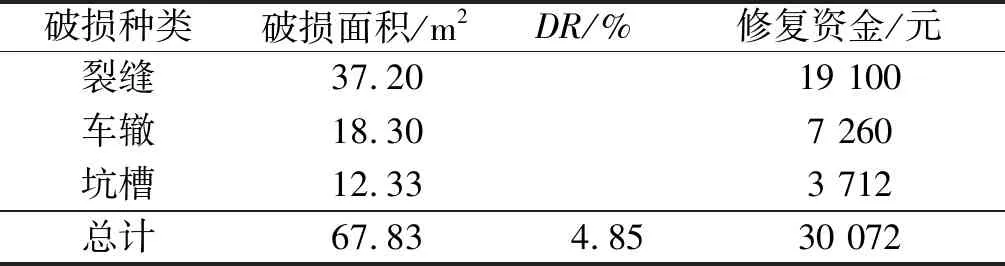
表2 湛徐高速公路部分路段基年路面破损状况
由表2可知:基年内各类破损的全部维修费用为30 072元,将其定为维修资金额度,作为后续维修费用分配的基础。采用蚁群算法,建立相关约束条件,以目标路段PCI指数的平均值为目标进行有限养护费用年度优化分配。
2.2 费用分配约束要求
基于基年内公路现状选择5年规划期进行费用分配。该项目为沥青路面,在基年破损基础上进行养护,运营一段时间后其性能逐步降低,尤其是车辆荷载增多后,路面性能下降更明显,需针对病害特点及时进行修复。由于路面养护费用有限,若现有养护费用得不到科学分配,则很难维持路面性能。为此,设置两种费用约束水平(见表3),基于固定的养护费用,对5年规划期内年度养护费用进行分配,通过不同年度养护费用的投入获得5年规划期内满足一定约束条件的路面状况。

表3 规划期内费用分配约束水平
2.3 中长期养护费用分配
2.3.1 水平1约束下养护费用分配
水平1约束下费用较充足,考虑到基年内养护费用较高,若按照基年修复标准,则规划期内后几年养护费用基本上分配不到,故将养护费用标准提高到32 000元;同时要求规划期内PCI值均大于90。将以上约束条件代入蚁群算法中进行计算,经过300次进化代数后的PCI均值见图1。
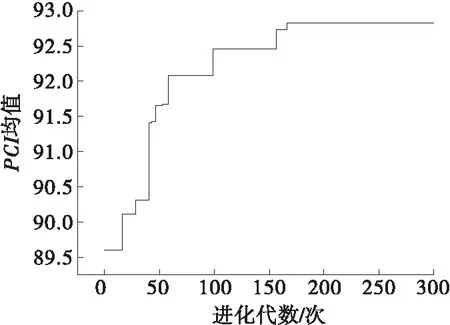
图1 水平1约束下蚁群算法运算后的PCI均值
由图1可知:在运算初期,PCI值为89.6;随着进化代数的增大,PCI值增大,进化代数达到180次左右时PCI值趋于稳定,为92.8左右,可认为PCI=92.8为蚁群算法最优解。对应的5年规划期内养护费用分配结果见表4,表4养护费用分配情景下5年规划期内路面状况指数见表5。
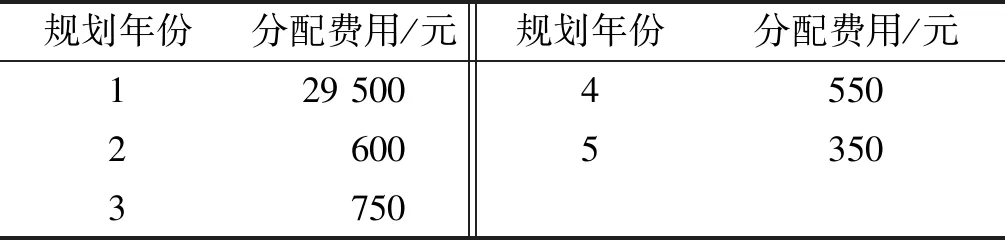
表4 水平1约束下各规划年度养护费用分配结果
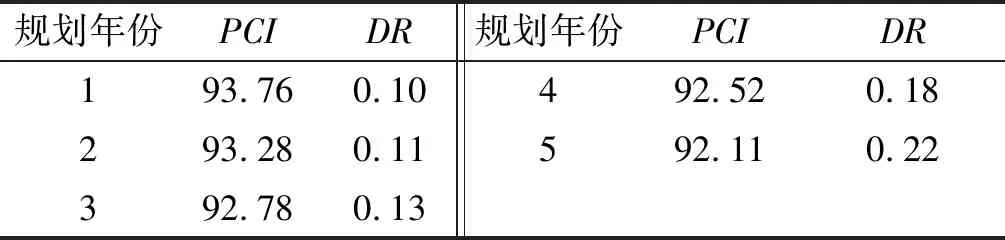
表5 水平1约束下各规划年度养护后的PCI值
由表4可知:水平1约束下,养护费用较充足时,第1年规划内养护费用分配值最大,占整个养护费用的93%左右;其余4年的养护费用均较小,且相差不大。
由表5可知:第1年养护后PCI值为93.76,DR值仅为0.1,满足表2中约束要求;随后4年的PCI值逐渐减小,但均大于90,满足约束要求。
造成以上养护费用分配差异大的原因是基年内路面病害多,养护工作量大,通过分配较多的养护费用使路面PCI值达到既定要求后,后续规划年内的养护工作量不大,因而维持较高路面质量所需养护费用较少。该费用分配结果与实际养护费用分配情况相符。
在费用较充足的水平1下进行蚁群算法分析,可获得与实际相近的费用分配结果。但蚁群分配计算较粗糙,可结合实际经验进一步精确。
2.3.2 水平2约束下养护费用分配
水平2约束下养护费用偏紧,同时PCI值达到表2中要求。考虑到基年内维修费为30 072元,在费用偏紧情况下设置30 000、28 000、25 000元3种养护费用,采用蚁群算法建立模型,计算3种养护费用下5年规划期内费用分配和对应的PCI值。计算中为追求费用分配最大效益,使各年度路面PCI均值最大,同时确保对应的PCI最小值尽可能大。水平2约束下养护费用分配结果及PCI值计算结果分别见图2、图3。
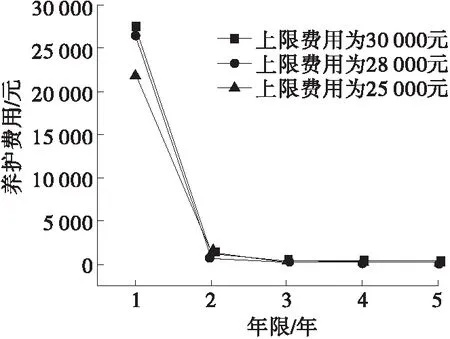
图2 水平约束2下各规划年度养护费用分配结果

图3 水平约束2下各规划年度PCI值
由图2、图3可知:不同上限养护费用下各规划年度内养护费用分配比例较接近,均为第1年养护费用最大,占比达90%以上,其余4年内分配费用相当。这种养护费用分配趋势与实际分配接近。养护费用上限值影响路面PCI值,上限费用越高,PCI值越大,上限费用为30 000元时第1年PCI值比上限费用为25 000元时第1年PCI值高6.5左右,且上限养护费用越低,规划期内PCI值下降越明显。3种养护费用下5年规划期内PCI最小值分别为92、86、81,均满足水平约束2的要求。
3 结论
(1) 可采用蚁群算法在确定路面养护费用上限值后对路面规划期内养护费用进行最大效益化分配;若养护费用不明确,可采用蚁群算法基于PCI值等指标提供多个养护水平进行养护费用分配。
(2) 湛徐高速公路的养护费用较充足及一般的情况下,规划期内第1年养护费用分配值均最大,超过总费用的90%,后期各年养护费用相当;规划期总的养护费用水平越高,各年度PCI均值越高;上限养护费用越低,规划期内PCI值下降越明显。
