高雷诺数湍流非预混火焰及NO生成的大涡模拟

于 洲, 黄立航, 叶桃红, 朱旻明

(中国科学技术大学 热科学和能源工程系, 合肥 230027)

0 引 言

日益严格的排放标准对燃烧设备提出了更高的要求，如何控制污染物排放，尤其是氮氧化物NOx的排放一直是学者研究的重点。优化燃烧器设计、探寻控制污染物排放的途径均有赖于数值模拟的开展[1]。大涡模拟(Large Eddy Simulation，LES)方法通过过滤操作将小尺度脉动和大尺度结构分开考虑，在计算量可接受的前提下，能够很好地捕捉流场结构和描述非稳态过程，对工程设计提供更多有益帮助[2]。

湍流燃烧的大涡模拟中的亚网格燃烧模型需要解决以下两个问题：(1)大涡模拟网格尺度下模化化学反应源项；(2)高效地考虑详细化学反应机理的影响[3]。化学建表方法(Tabulated Chemistry)和过滤密度函数(Filtered Density Function，FDF)方法是两种代表性的湍流燃烧模型。化学建表方法通过流形的概念，选取若干个特征标量描述湍流燃烧过程，结合假定概率密度函数模型描述湍流与火焰的相互作用，可以简单高效地考虑详细化学反应机理[4]影响。过滤密度函数方法用随机运动的拉格朗日粒子描述湍流燃烧场，采用蒙特卡洛方法求解粒子的随机微分方程(Stochastic Differential Equation, SDE)，化学反应源项可直接求解，能更好地表征有限化学反应速率过程[5]。但传统的FDF方法需要的随机粒子数目极多，通常在一个大涡模拟网格内需要有几十个粒子。为了简化计算量，Cleary等[6]提出了稀疏拉格朗日FDF方法，即数个大涡模拟网格共用一个粒子。

除了描述火焰结构，污染物如氮氧化物排放的计算也是湍流燃烧模型一个重要方面。氮氧化物NOx主要包括N2O、NO、NO2等，其中NO的含量最高。按照特征时间尺度的不同，NO生成过程通常可以分为两大类。第一类为快速型NO，该类的特征时间尺度与C元素反应的特征时间尺度相近。另一类NO在燃烧放热完成后的燃尽区生成，该类的NO生成量相对较多且其特征时间尺度更长。对于不含N元素的燃料而言，在火焰面区域内快速型NO的生成属于Fenimore机制。快速型NO的生成与N元素反应和C元素反应之间的相互耦合有关。燃尽区包含了其他的化学反应过程，在该区域内可能产生占总数90%甚至更多的NO。此时NO生成机制主要是Zeldovich机制，其中N2O、NNH路径为主导因素[7]。因为NO生成的复杂性，发展精细的模拟NO的数值方法仍备受关注。

Sandia甲烷/空气值班射流系列火焰是经典的湍流非预混(TNF3)火焰，实验主要研究了射流雷诺数对非预混火焰的影响，涉及局部熄火、局部再燃等现象，给出了详细的速度、温度以及包括污染物NO在内的组分等实验数据[8-9]。近期关于Sandia系列火焰数值模拟工作[10-12]主要集中在发展湍流非预混燃烧模型，分析湍流非预混火焰中污染物生成特性。

本文通过大涡模拟方法，分别采用化学建表方法结合假定概率密度模型和稀疏拉格朗日FDF方法，对高雷诺数湍流非预混火焰Flame D进行研究。在第一种模型中，探讨了不同假定概率密度函数的影响，而在第二种模型中验证了改进的密度耦合方法的可行性。同时比较了两类亚网格燃烧模型预测氮氧化物的能力。本文旨在定量比较两类亚网格燃烧模型的差异，并基于大涡模拟结果对湍流非预混火焰特征、污染生物生成特性进行分析。

1 Sandia甲烷/空气值班火焰简介

Sandia甲烷/空气值班系列火焰由三股流体组成，包括体积比为3∶1的甲烷/空气中心射流、温度约为1880 K的值班火焰产物以及常温常压空气伴流。其中，中心射流管内径D=7.2 mm，值班火焰产物流经内径为7.7 mm、外径为18.2 mm的圆环，值班火焰的焓值及组分与φ=0.77的甲烷/空气的燃烧产物相近。具体实验入口速度参数见表1。

表1 Flame D的入口速度Table 1 Inlet velocities of Flame D

表中Uj、Up、UCO分别为中心射流速度、值班火焰速度、空气伴流速度，其单位均为m/s。Rej为中心射流雷诺数。各入口温度及组分质量分数见表2。

表2 Flame D各入口温度及质量分数Table 2 Inlet temperatures and mass fractions of Flame D

表中Main、Pilot、Coflow分别对应中心射流、值班火焰及空气伴流。

2 亚网格燃烧模型

2.1 化学建表方法和假定概率密度函数模型

不同化学建表方法的区别主要体现在所选取的原型火焰不同。Sandia甲烷/空气值班系列火焰是典型的非预混火焰，但其中心射流组分并不是纯燃料，其中也包含了一定量的氧气。Vreman等[13]分别采用预混和非预混火焰面生成流型方法对Sandia系列火焰中的Flame D和F进行大涡模拟研究，指出基于预混火焰面生成流型方法同样可以得到令人满意的模拟结果。因此，本文采用预混火焰面流型生成方法(premixed FGM，PFGM)构建化学热力学表，化学反应机理采用广泛应用的GRI3.0机理。用FlameMaster程序计算一系列不同当量比的一维无拉伸层流预混火焰获得层流原始火焰数据。当量比范围覆盖贫燃极限(φ=0.40)至中心射流燃料当量比(φ=3.17)。

基于上述原始数据，本章采用混合物分数Z及反应进度变量c构建低维流型。定义中心射流、空气伴流的混合物分数Z分别为1和0，反应进度变量表示成主要组分线性组合的形式。因此，层流化学热力学表可以表示成φ=φ(Z,c)。通过假定概率密度函数模型描述物理量的亚网格分布，以考虑湍流与火焰的相互作用。混合物分数Z与反应进度变量c的联合概率密度函数简化成二者边缘概率密度函数乘积的形式。不同边缘概率密度函数的影响需要进行定量比较。本文分别采用三种函数模化边缘概率密度函数，即Dirac函数、Beta函数和Top-hat函数。Dirac函数不需要考虑方差的影响，需要求解的特征标量方程更少，有利于节省计算资源。Beta函数和Dirac函数的形式可参考文献[14-15]，本文只给出Top-hat函数的形式。

Top-hat函数源于亚网格线性分布思想，其优势主要在于形式简单且与LES过滤操作有更好的相容性[16]。Floyd等[16]定量对比了Top-hat函数和Beta函数作为混合分数的假定概率密度函数的结果，指出Top-hat函数也可以很好地描述混合分数的亚网格分布。随后，Olbricht等[17]和Rittler等[18]也验证了Top-hat函数作为反应进度变量的假定概率密度函数的可行性。假定混合物分数与反应进度变量的概率密度函数均为Top-hat函数，

(1)

式中f表示混合物分数或反应进度变量。Top-hat函数的上下限fa、fb可由下式计算:

(2)

(3)

(4)

(5)

(6)

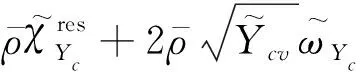
(7)

2.2 稀疏拉格朗日FDF模型

稀疏拉格朗日FDF方法中，用大涡模拟求解Favre过滤的连续性方程、动量方程以及混合物分数方程。除此之外，采用蒙特卡洛方法求解描述粒子运动的随机微分方程，包括颗粒在物理空间上的运动，以及颗粒上标量的变化。其中颗粒位置Xi(t)的随机微分方程为:

(8)

式中D和Dt分别是分子扩散系数和湍流扩散系数，右边第一项代表对流运动以及扩散带来的在物理空间上的确定性运动，第二项以随机游走过程模拟扩散带来的平均值变化，dWi表示随机的Wiener过程。

颗粒上第α种标量φα(t)变化由混合过程dM与化学反应dS两部分组成，

dφα(t)=dM+dS

(9)

式中dM由混合模型封闭，本文采用广义MMC模型[6]。如前所述，dS不需要模型，可以采用直接积分，处理任意化学反应机理。

在稀疏颗粒方法中，颗粒之间的距离比LES网格尺寸大，所以采用广义MMC模型来保证混合的当地性[19]。广义MMC模型将LES计算的混合物分数插值得到颗粒上的参考变量，结合参考变量空间和三维物理空间上的距离，以Curl模型构造，进行两两配对，其形式如下:

(10)

(11)

本文采用改进的密度耦合方法将粒子热释放产生的密度变化引入到LES计算中[20]。将拉格朗日颗粒得到的等效焓源项，替代到LES的过滤得等效焓输运方程中的源项，实现拉格朗日框架向欧拉框架的耦合。其中比等效焓定义如下[21]：

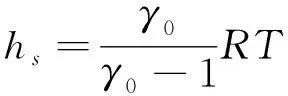
(12)

式中γ0为比热比，R为气体常数，T表示温度。其Favre过滤的输运方程为，

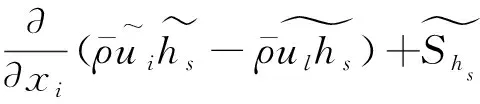
(13)

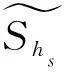
对于LES网格上的用于迭代的密度直接使用该网格上的等效焓值按照式(14)计算得到，完成整个密度耦合过程。

(14)

2.3 NO输运方程及模化方式

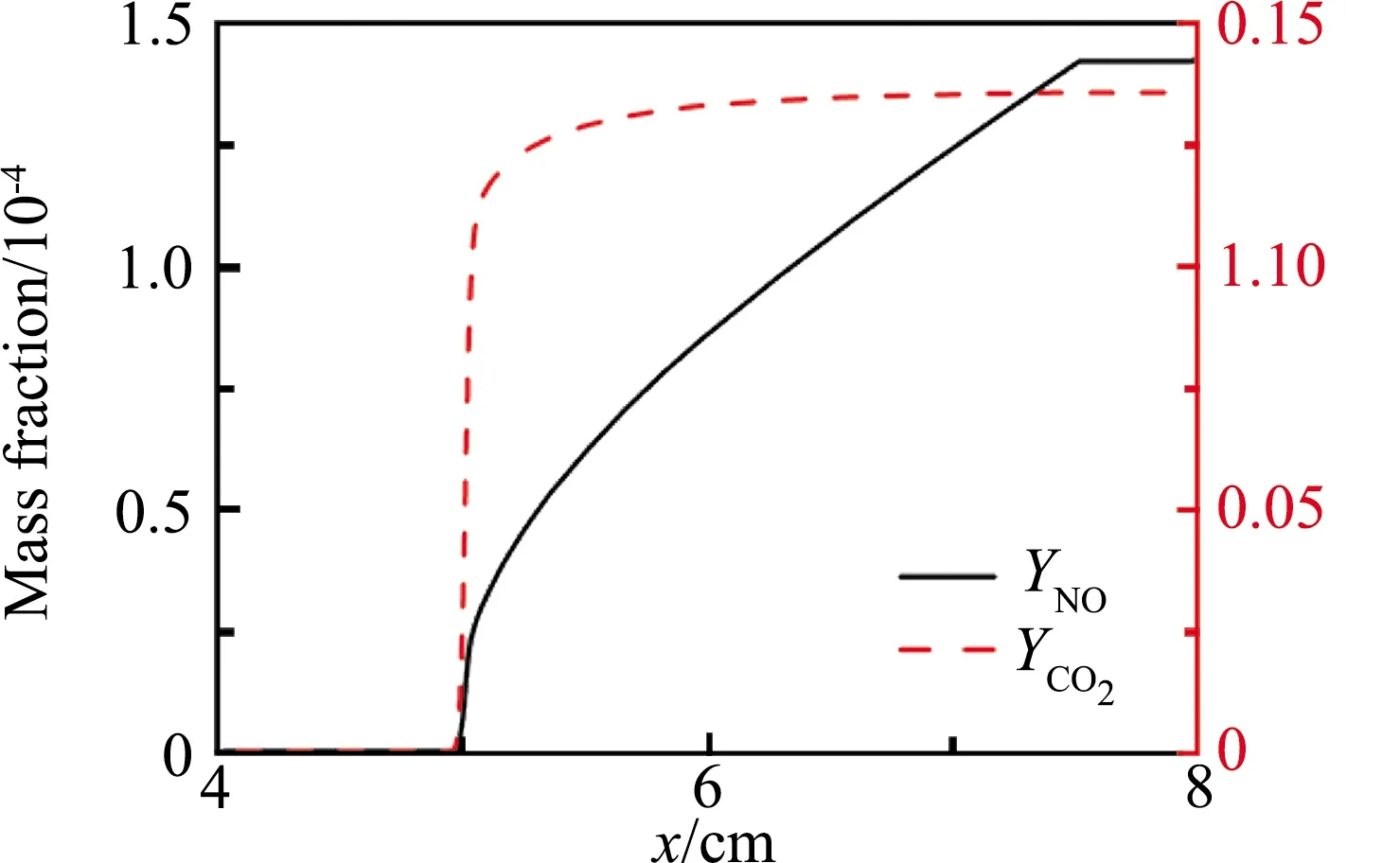
(a) NO、CO2质量分数在物理空间分布

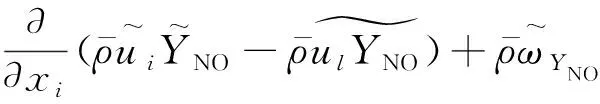
(15)

对于稀疏拉格朗日FDF方法而言，只需采用包含NO相关基元反应的化学反应机理即可。

图2 湍流化学热力学表中未归一化的反应进度变量和组分NO的化学反应源项分布

3 数值方法及算例设置

本文所有大涡模拟算例均基于自主开发的Fortran程序开展[24-27]。动量方程的时间与空间离散均为二阶格式，标量方程的空间离散使用三阶WENO格式。蒙特卡洛方法中，颗粒运动的SDE(式8)采用弱一阶显式求解，颗粒上的参考变量以及速度由LES计算的过滤值经三阶插值得到。计算过程中动态调节时间步长，以保证CFL数小于0.2。基于化学建表方法的算例计算区域为轴向长度600 mm、半径300 mm的圆柱体。采用结构化网格划分计算区域，在射流出口和剪切层附近等梯度较大区域进行加密。轴向、径向采用312×161个非均匀网格，周向采用64个均匀网格，网格总数约为330万，最小网格尺寸为0.12 mm。为了降低计算耗时，基于稀疏拉格朗日FDF方法的算例所采用的圆柱体计算域相对较小，计算域轴向长度为252 mm，径向为108 mm，轴向、径向和周向的网格划分为500×85×32，网格总数约为136万。参考已开展的Flame D大涡模拟计算工作[11]，本文所采用的网格分辨率可满足相关计算的要求。

计算域出口采用对流边界条件，侧边界采用滑移边界条件，管壁处采用无滑移条件。通过预计算的充分发展管流出口数据作为中心射流的速度入口条件，高温伴流入口速度通过1/7次方分布的平均速度与白噪声叠加确定，空气伴流入口平均速度采用实验中的体积流速。在稀疏颗粒方法的初始场中，按照大约八个网格一个颗粒(1L/8E)的比例设定颗粒，入口处的颗粒质量按照入口附近的网格以同一比例(1L/8E)设定。燃烧场经过10个特征流动时间达到充分发展，为保证统计结果的有效性，统计过程持续10个特征流动时间。本文共设置4个大涡模拟算例，见表3。

表3 大涡模拟算例汇总Table 3 Summary of LES cases

4 结果与讨论

4.1 统计结果及模型评价

图3展示了不同算例预测的Flame D的温度及其脉动，组分NO、H2O及CO质量分数在轴向位置7.5D、15D、30D、45D、60D、75D处的径向分布。需要说明的是，因为稀疏拉格朗日FPF方法计算量较大，因此所设置的计算域较短，只在前三个截面进行两种亚网格模型的比较。首先看轴向位置7.5D、15D、30D的结果，稀疏拉格朗日FDF方法可以很好地表征有限化学速率，其组分H2O及CO质量分数模拟结果优于化学建表方法结合假定概率密度函数模型。而NO质量分数的在轴向位置15D、30D的偏差可能与所采用的混合时间尺度模型有关。除了轴向位置上均相近，其中Beta函数的表现略优，即不同假定PDF均可合理描述湍流与火焰的相互作用。由于PFGM模型并不考虑拉伸作用的影响，因此在下游处，预测的温度略高。而不同假定PDF预测的NO质量分数分布差别较大。所有轴向位置上Dirac函数均远高估了NO的生成，而Top-hat函数在大部分轴向位置上均低估了NO的生成，只在最下游75D处相对准确预测了NO质量分数分布。相比而言，Beta函数对于NO的预测更加合理。因此接下来的分析均基于PFGM模型耦合假定Beta函数得到的数据。

(a) x=7.5D

4.2 火焰结构表征

图4给出了Flame D的混合物分数、温度、NO质量分数的瞬时及统计平均云图，图中黑色实线为当量混合线(Zst=0.351)。从图中可以观察到，Flame D的高温区及NO质量分数较大的区域主要分布在当量混合线及富燃侧附近，这也体现出其非预混燃烧的本质，说明基于PFGM模型模拟该火焰具有合理性。除此之外，从瞬时温度局部放大图(图5)可以看出Flame D的局部熄火现象并不明显。

为了进一步定量分析温度、组分等物理量与混合物分数的关系，图6给出了不同轴向位置Flame D的温度及NO质量分数在混合物分数空间的条件平均分布，图中黑色虚线为当量混合线。可以看出，LES得到的温度条件平均分布与实验高度吻合，其最大值位于当量混合附近，这符合非预混燃烧的基本性质。LES得到的NO质量分数条件平均分布与实验值存在一定偏差，但二者的规律相近，最大值位于当量混合处或靠近当量混合的富燃侧。

(a) 瞬时云图

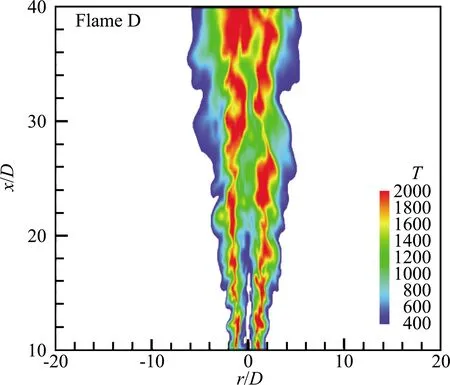
图5 Flame D瞬时温度局部放大图 Fig.5 Partial enlarged drawing of instantaneous temperature of Flame D

4.3 污染物NO生成特性分析

图7给出了不同轴向位置Flame D的NO质量分数在温度空间的散点分布，图中红色点划线为散点分布的多项式拟合。可以看出，NO质量分数与温度呈正相关。在x=15D处，NO质量分数与温度近似呈线性关系。而在x=30D和x=45D处，由于燃烧作用的影响，在高温区NO质量分数与温度的非线性程度增强。在下游x=60D处，NO质量分数与温度近似呈多项式关系。

(a) x=15D

(a) x=15D (b) x=30D

为探讨NO质量分数与主要标量之间的关系，表4给出了不同轴向位置Flame D的主要标量与NO质量分数的皮尔森相关系数[28]。皮尔森相关系数定义如下:

图8 Flame D火焰区域内当量混合处NO质量分数在混合物分数标量耗散率空间的散点分布

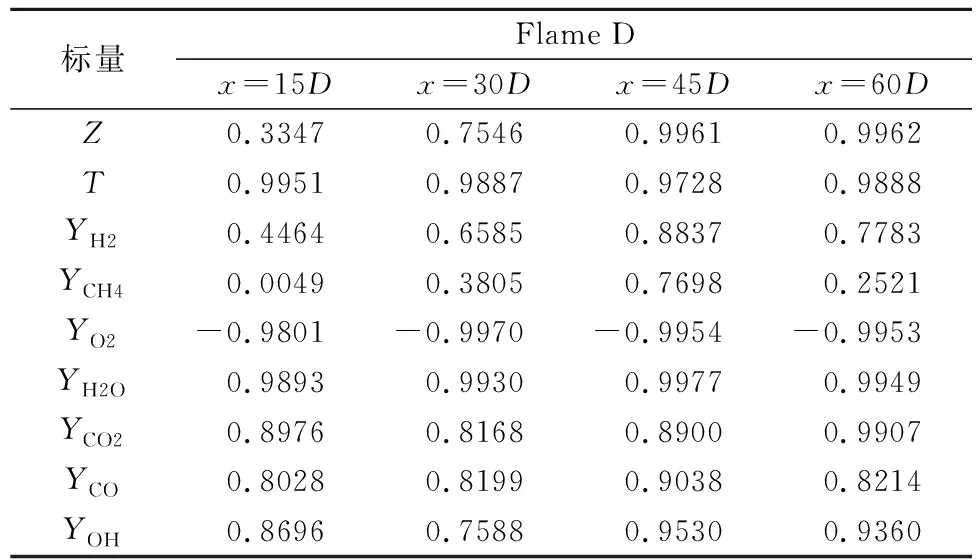
表4 Flame D不同轴向位置上主要标量与NO质量分数的皮尔森相关系数Table 4 Pearson correlation coefficients between major scalars and NO mass fraction at different axial locations of Flame D

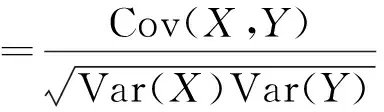
(16)

式中Cov表示协方差，Var表示方差。

一般来说，混合物分数和温度是影响燃烧进程的两大主要因素，在x=15D处，NO质量分数与混合物分数的相关程度不高。随着流场向下游发展，二者的相关程度增加。而由于高温伴流的影响，NO质量分数与温度一直保持高度相关。在不同截面上，反应物的O2和生成物的H2O均与NO高度相关。

5 结 论

本文分别采用化学建表方法耦合假定概率密度函数模型和稀疏拉格朗日FDF方法对Sandia甲烷/空气值班射流火焰的Flame D进行大涡模拟研究，通过求解附加的NO输运方程模拟污染物NO的生成，系统比较了亚网格燃烧模型、假定概率密度函数对火焰结构和污染物模拟的影响。相关结论如下：

1) 通过比较不同模型的统计结果可以发现，不同亚网格燃烧模型预测的温度及大组分相近，稀疏拉格朗日FDF方法可以更好地模拟CO质量分数分布。结果验证了改进的密度耦合方法可以较好实现LES场和颗粒场的数据耦合。稀疏拉格朗日FDF方法可以很好地表征有限化学反应速率。不同假定PDF均可合理描述湍流与火焰的相互作用，差别主要体现在模拟NO分布，Dirac函数远高估了NO生成，而Top-hat函数则略低估了NO生成，Beta函数表现最优。

2) 由云图和散点分布可知，Flame D的高温区及NO质量分数较大的区域均主要分布在当量混合线及富燃侧附近，其局部熄火现象并不明显。

3) 由散点分布可知，NO质量分数与温度呈正相关。在x=15D处，NO质量分数与温度近似呈线性关系。而在x=30D和x=45D处，由于燃烧作用的影响，在高温区NO质量分数与温度的非线性程度增强。在下游x=60D处，NO质量分数与温度近似呈多项式关系。NO质量分数在标量耗散率空间下首先快速衰减，随后近似不变，其峰值主要集中在标量耗散率很小的区域。由皮尔森相关系数可知，由于高温伴流的影响，NO质量分数与温度一直保持高度相关。在不同截面上，作为反应物的O2和生成物的H2O均与NO高度相关。

致谢:本文的数值模拟工作得到中国科学技术大学超级计算中心的大力支持。