基于非协调广义混合元的含孔平板应力分析

姚玉卿 光辉 王绍波

摘 要：首先，根据广义HR变分原理建立了用于分析二维平面问题的非协调广义混合元。然后，应用该混合元对中心含孔平板的应力及应力集中系数等问题进行了详细的分析，并与二维的非协调位移元的结果进行了比较。在有限元模型相同的情况下，非协调广义混合元的结果精度明显优于常规的非协调位移元。另一方面，为了回避混合元法要求计算机内存空间较大的问题，提出了结构的局部区域非协调广义混合元方法。数值实例表明，局部区域非协调广义混合元方法是可靠的。

关键词：有限元方法;广义混合元;非协调广义混合元;含孔平板;应力集中系数

中图分类号：V257;O343.4文献标识码：A

Stress Analysis of Plate witha hole Based

on Incompatible Generalized Mixed Element

Yao Yuzhe Qing Guanghui* Wang Shaobo

College of Aeronautical Engineering，CAUC Tianjin 300300

Abstract：Firstly，based on the generalized HR variational principle，a nonconforming generalized mixed element is established for the analysis of twodimensional problems.Then，the mixed element is applied to analyze the stress and stress concentration factor of the central plate with holes in detail，and the results are compared with those of the twodimensional incompatible displacement element.In the case of the same finite element model，the result accuracy of the incompatible generalized mixed element is obviously better than that of the conventional incompatible displacement element.On the other hand，in order to avoid the problem that the mixed element method requires large memory space，a local incompatible generalized mixed element method is proposed.The numerical examples show that the local incompatible generalized mixed element method is reliable.

Key words：finite Element method;generalized mixed element;nonconforming generalized mixed element;plate with a hole;stress concentration factor

为了满足装配或服役过程中的维护修理等方面的要求，在现代工程结构，尤其是飞机器这类复杂的工程结构，常常要求在结构的零部件上打孔或开口。这些孔或开口的出现势必导致对结构寿命有着重要影响的应力集中问题。对于含有多个孔或复杂开口的零部件，人们通常采用试验或有限元数值方法分析其应力集中问题。在网格较稀疏的情况下，最常见的位移有限元法[1]的结果往往不是很理想。实质上，通常的位移有限元法求得的位移精度高，但是应力精度比位移精度差一个阶次，这是由于节点的应力结果是依据本构关系逐一单元计算的，因而造成连接多个单元的同一节点上出现了不同的应力结果，所以必须对节点应力进行恢复或磨平的操作。另一方面，这种依据本构关系计算应力的方案，不便引入应力边界条件。因此，研究探索更为有效和可靠的新方法具有重要的工程意义。

荣廷玉、党发宁和Felippa等人[25]最先提出了用于分析二维问题的广义混合元。用于分析三维问题的非协调广义混合元[69]是在三维广义混合元的基础上对位移变量的插值函数增加非协调项而建立的。一方面，在计算量增加不多的情况下，单元的精度得到了进一步提高。另一方面，非协调广义混合元可克服剪切锁死问题。不论是二维的、三维的广义混合元还是非协调广义混合元，其共同优点是，与位移元相比较，在网格较稀疏的情况下，能给出更为精确的应力结果，位移值和应力值是同时求得的，且稳定性好，收敛快[29]。但是，由于基于混合元的线性系统方程包含了位移和应力两类变量，所以这类方法需要的计算机内存空间相對较大。

实际上，对于一般的工程结构问题，设计人员并不一定要分析结构所有位置的应力结果。所以，针对结构的开口、孔和裂纹尖端等高应力区域，可以进一步探索节省计算机内存的局部区域的混合元法。

1 基础理论

1.1 二维问题的广义HR变分原理

忽略体积力，并且假设位移边界条件u-u-=0，则广义HR变分原理为[2]：

ΠGHR=V[-12σTSσ+σT（SymbolQC@

u）]dV+vλ（12σTSσ+12（SymbolQC@

u）TC（SymbolQC@

u）-σT（SymbolQC@

u））dV-SσT-TudS（1）

式中，u=[u1 u2]T为位移向量，SymbolQC@

为微分操作矩阵，C为材料刚度矩阵，S=C1，V代表体积，S表示平板类结构的面积，T-=[T-1 T-2]T是作用平板类结构在侧面的已知面力。

1.2 非协调广义混合元

四边形单元的非协调位移场可以表示为[10，11]

u=Nqe+Nrre（2）

其中，qe为单元的位移向量，re为在单元内部增加的结点位移向量，N和Nr分别为单元节点和内部节点的插值函数矩阵。

假设应力变量的插值函数与位移变量插值函数的协调部分相同，则单元应力向量的近似表达式为

σ=Mpe（3）

式中，M是用于表示应力向量（σ11，σ22，σ12）的插值函数矩阵，pe为单元的应力向量。

根据文献[5]，当式（1）中的λ=0.25时，数值结果精度最好。将式（2）和式（3）代入式（1），并取λ=0.25，可得到广义HR变分原理的离散形式：

∏GHR（pe，qe，re）=∑ni=1-38pTeKpppe+34pTeKpqqe

+34pTeKprre+34qTeKqrre

+18qTeKqqqe+18rTeKrrre

-fTeqe（4）

式中，

Kpp=ViMTC-1MdV，

Kpq=ViMT（SymbolQC@

N）dV，

Kpr=ViMT（SymbolQC@

Nr）dV，

Kqr=Vi（SymbolQC@

N）TC（SymbolQC@

Nr）dV，

Kqq=Vi（SymbolQC@

N）TC（SymbolQC@

N）dV，

Krr=Vi（SymbolQC@

Nr）TC（SymbolQC@

Nr）dV，

fe=SσiNTT-dS。

对上式pe，qe，re进行变分，化简后可得二维问题的非协调广义混合元列式：

-6Rpp 6Rpq

6RTpq Rqqpe

qe=0

8fq（5）

式中，Rpp=Kpp，

Rpq=Kpq-KqrK1rrKTpr，

Rqq=Kqq-KqrK1rrKTqr。

2 数值实例

例题1 中心含圆孔的方形有限平板，板的边长为2a，两端受均布拉伸载荷σ0作用，如图1所示。圆孔的半径r=a/50，材料杨氏模量E=210.0，泊松比μ=0.3。

根据文献[12]，在极坐标系下，受均匀拉伸作用的含小圆孔无限大平板的应力解析解为：

σ11=σ02（1-r2ρ2）+σ02（1+3r4ρ4-4r2ρ2）cos2θ

σ22=σ02（1+r2ρ2）-σ02（1+3r4ρ4）cos2θ

σ12=σ21=-σ02（1-3r4ρ4+2r2ρ2）sin2θ（6）

其中，r为小圆孔的半径。

考虑结构的对称性，四分之一的网格模型如图2所示。靠近圆孔边界上的单元于x1方向和x2方向的长度是其他单元相应长度的一半。

这里考虑平面应变问题。表1列出了商用软件ABAQUS中二维非协调位移元（NCE4）和本文的二维非协调广义混合元（NCME4）两种方法的α点的应力集中系数。β点的应力结果列于表2。表1和表2中的精确解由式（6）得到。必须说明，二维的非协调位移元法（NCE4）的节点应力值是对高斯点应力采用外推法得到的。

从表1和表2中的结果可以看出，非协调位移元在α点的应力集中系数和β点的应力结果均都偏小，这主要是因为位移元的刚度大。表1表明，非协调广义混合元的结果大于理论应力集中系数，这是由于本例分析的是有限尺寸的平板，而理论上的应力集中系数是以假设无限大平板为前提的。如果考虑孔的影响，NCME4的应力集中系数结果（参见表1的第3列）和β点的应力结果（参见表2的第3列）均比NCE4更接近精确解。

例题2中心含圆孔的无限大平板受单轴均匀拉伸载荷作用，如图3（a）所示。材料杨氏模量E=1000，泊松比μ=0.3。这里仅对如图3（b）所示的靠近孔周围的子区域进行数值计算。

图4给出了三种网格模型以及相应的位移边界条件和应力边界条件。通过精确解公式（6）可以计算出边界BC和CD各个节点的应力结果。这些结果作为模型边界BC和CD上节点的载荷。

这里采用NCME4对图4（a）、（b）和（c）等三种网格密度不同的模型进行分析。

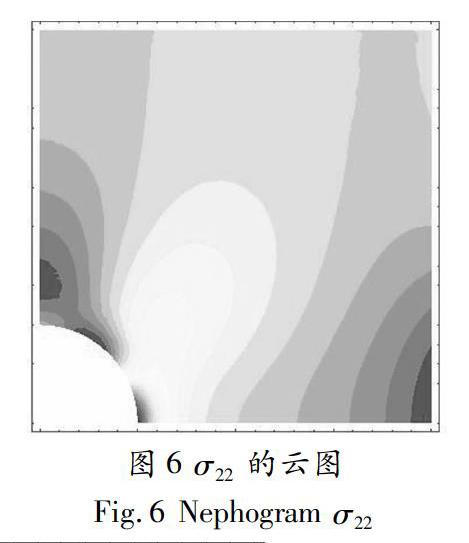
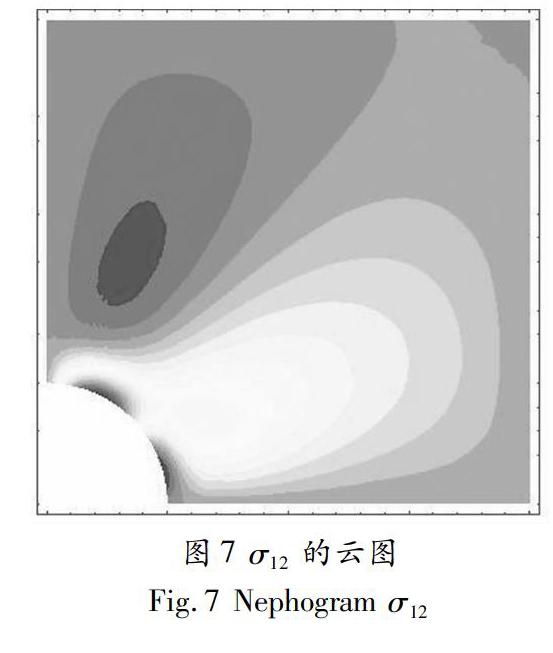
根据网格模型4（c）的应力结果所绘制出的应力云图见图5至图7。

圖5至图7的三个应力云图直观地表明：NCME4的结果比较真实可靠，尤其是模型边界处，应力云图更真实。这是由于基于NCME4的有限元混合模型可方便地引入应力边界条件。

为了进一步分析NCME4的优越性，在表3至表5中详细列出三种网格模型P点（x1=1.0606602，x2=1.0606602或ρ=1.5，θ=45°）处，NCE4和NCME4两种方法的σ11、σ22和σ12的数值结果。

表3至表5中，σG、σE和σP分别表示非协调位移元法求结构节点位移之后，采用总体磨平、单元磨平和分片磨平等方案所得P点的应力结果。

表3至表5中的数据表明，与非协调位移元的结果相比，本文的非协调广义混合元的结果更精确。

例题3 中心含孔板的材料以及三种网格模型、位移和应力边界条件与例题2相同。

下面考虑对局部区域采用非协调广义混合元计算应力的方法。即先用非协调位移元NCE4计算图4中三个模型的节点位移，然后利用NCME4分析图8所示模型中的粗实线所包围区域的节点应力。这里称这种局部区域采用非协调广义混合元的方案为局部非协调广义混合元法（LNCME4）。必须指出：图8中各模型的粗实线是局部模型的边界线，这些边界线上节点的位移是已知的，被作为局部模型的位移边界条件处理。

表6和表7分别给出了非协调位移元、非协调广义混合元和局部非协调广义混合元（LNCME4）等方法在α点σ11和β点σ22的数值结果。

表6和表7表明，非协调广义混合元方法和局部非协调广义混合元方法在α和β两点处的σ11和σ22的精度相差不大。事实上，就图8（a）这个网格较稀疏的模型而言，非协调广义混合元法和局部非协调广义混合元法的结果与精确解的最大误差分别为1.3%和2.3%。但是局部非协调广义混合元法在节省计算机资源方面有一定的优势。

3 结论

本文首先根据广义HR变分原理建立了用于分析二维问题的非协调广义混合元，并应用该单元对中心含孔平板的应力进行了详细的分析。具体结论包括：

（1）有限元网模型相同的情况下，二维问题的非协调广义混合元的应力结果精度明显优于常规的非协调位移元;

（2）数值实例表明：本文提出的局部区域采用非协调广义混合元的方法的应力结果精度也高于非协调位移元。这种局部区域方法可以很简便地扩展用于分析具有其他形式的局部高应力区域结构的应力问题。

参考文献：

[1]Zienkiewicz O C，Taylor R L，Zhu J Z.The finite element method：Its basis and fundamentals，sixth edition[M].The finite element method：its basis and fundamentals（Seventh Edition）.2005.

[2]荣廷玉.弹性力学广义混合变分原理及有限元广义混合法[J].力学进展，1987，17（2）：186199.

[3]党发宁，荣廷玉，孙训方.Reissner板问题的有限元广义混合法[J].计算力学学报，2000，17（2）：218222.

[4]黨发宁，李宁，荣廷玉.广义混合变分原理及其有限元法[J].自然科学进展，2002，12（3）：250254.

[5]Felippa C A.Parametrized multifield variational principles in elasticity：I.Mixed functionals[J].Communications in Applied Numerical Methods，1989，5（2）：7988.

[6]Qing G，Tian J.Highly accurate symplectic element based on two variational principles[J].Acta Mechanica Sinica，2018，34（1）：151161.

[7]刘艳红，李锐.含参数辛元与热弹性复合材料层合板分析[J].复合材料学报，2019，36（5）：13061312.

[8]Guanghui Qing，Junhui Mao，Yanhong Lui.Generalized mixed finite element method for 3D elasticity problems[J].Acta Mechanica Sinica，2018：34（2）：371380.

[9]赵直钦，卿光辉.改进的非协调广义混合单元及性能分析[J].应用数学与力学，2019，40（5）：518526.

[10]Theodore H.H.Pian，ChangChun Wu，hybrid and incompatible finite element methods[M].Chapman and Hall CRC，2005.

[11]陈万吉.一个高精度八结点六面体单元[J].力学学报，1982，18（3）：5867.

[12]吴家龙.弹性力学[M].北京：高等教育出版社，2001.

作者简介：姚玉喆（1993—），男，汉族，山东德州人，硕士研究生，研究方向：从事民机复合材设计与研究。

*通讯作者：卿光辉（1968—），男，汉族，湖南新化人，博士，教授，研究方向：复合材料结构力学。