点上着眼 法上着力 思想是关键

吴从洋 马娇娇

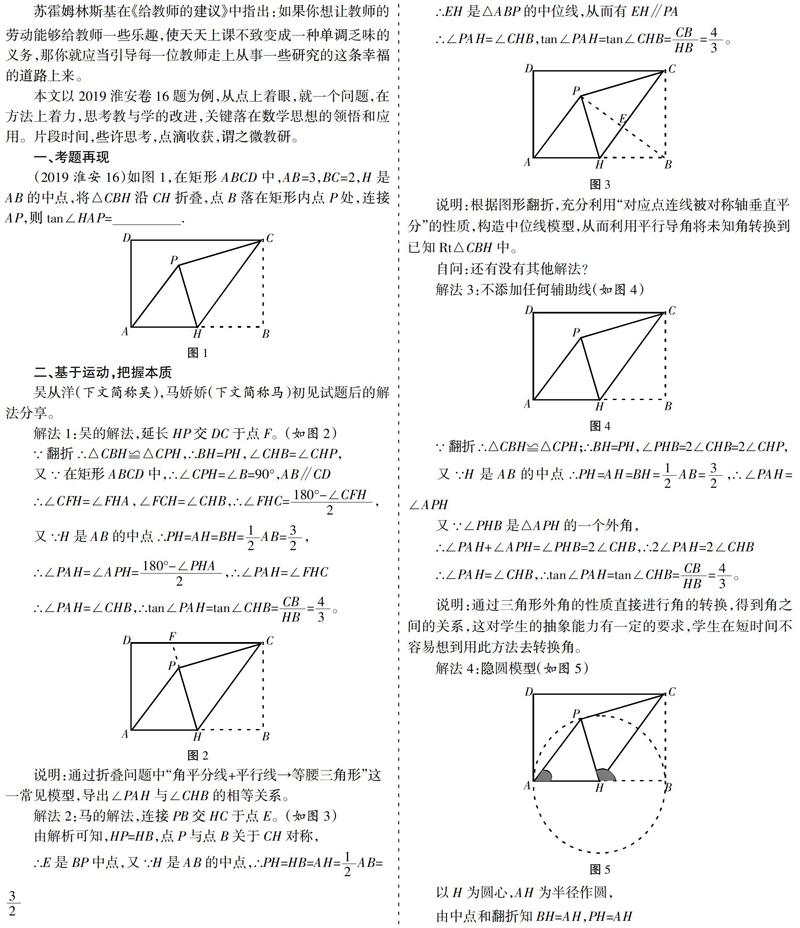
苏霍姆林斯基在《给教师的建议》中指出：如果你想让教师的劳动能够给教师一些乐趣，使天天上课不致变成一种单调乏味的义务，那你就应当引导每一位教师走上从事一些研究的这条幸福的道路上来。

本文以2019淮安卷16题为例，从点上着眼，就一个问题，在方法上着力，思考教与学的改进，关键落在数学思想的领悟和应用。片段时间，些许思考，点滴收获，谓之微教研。

说明：当一个图形中出现共端点3条线段为定长时，通常可以借助构造圆来解决问题。当圆出现后，可以运用圆周角定理等有关知识解决问题。可谓：见等长，现“圆”形。

三、拾级而上，顺藤摸瓜

对于学生来说，本道题对学生的抽象能力有一定的要求，如果学生不去分析图形元素之间的关系，很容易按部就班在原△APH中构造直角三角形，由于原三角形并不是可解三角形，故而需要借助勾股定理、相似等方法求得线段长，会增加解题时间。

下面将学生解题方法列举一二：

解法5：在解法2的辅助线基础上，未用E是BP中点这一性质。（图6）

从而根据同位角相等，也得两线平行，下同解法2。

说明：看到三条线段相等，便想到可以推导原三角形为直角三角形，再根据轴对称的垂直得到直角，从而得出直线平行，进而转角，但未能充分利用“对应点的连线被对称轴垂直平分”这一性质，推理略显复杂。

解法6：利用建系，直接求P点坐标。（如图7）

说明：建系是一种用代数方法解决几何问题的模型，在几何图形中，直线就是一次函数，求线段长可以转化为求解点坐标，但对学生的计算能力要求较高。

还有学生在解法2的辅助线作图基础上，结合勾股定理列方程解题，也有学生构造一线三等角模型，利用K型相似求出P所在的直角三角形的两条直角边长，但是计算相当冗长。为了让学生准确定位题目的考点，巧解难题，确实需要教师在教学时引导学生在点上着眼，法上着力。充分抓住运动中的不变量，才能做到妙构解法，轻松做题。

四、授之以鱼，不如授之以渔

课标中对图形变换思想提出了具体要求，图形变换思想是数学中的一种重要的思想方法，在教学中，向学生渗透图形变换思想，能够帮助学生发现图形之间的本质联系，提高抽象能力，促进思维发展。近几年，图形变换被多个省市选为中考压轴试题，可见，几何变换逐渐成为初中数学的热点学习内容。现以2016年山东威海一题为例加以说明：

如图8，在矩形ABCD中，AB=4，BC=6，点E为BC中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，求CF的长。

本题解法很多，构造中位线模型、等腰三角形模型或一线三等角相似模型，然后借助相似三角形、三角函数等性质解决问题。

识图、析图、构图是解决图形几何题的关键，遇翻折类问题，最核心的是研究翻折前与翻折后的变化，尤其是抓住翻折过程中的不变量——万变不离其宗，从而带来角相等、线段相等等几何元素的关系。常见处理策略有：

1.利用全等、垂直、中点等联想数学模型。

2.折叠就有角平分线，结合平行线，可得等腰三角形模型，结合等腰三角形“三线合一”定理、倍半角模型等解决问题。

3.如遇直角三角形折叠，可引申出一线三等角模型，借助K型相似，求出未知边角元素。

总之，充分利用折叠的性质，导边导角，可以妙构解法，轻松解题。

通过教师初见试题与学生初见试题后选取的解题思路进行比较，不难发现学生对于几何图形分析能力弱，思维固定，只注重解题，忽略数学模型的选择与思想的应用。这就要求教师在教学时注重图形变换思想的渗透，在实际教学过程中，图形变换思想的渗透不是几节专题课就能够讲明白的，而是要借助教材中的多个教学内容来完成渗透，这就要求教师平时认真研究教材，适时渗透图形变换思想。可以借助几何画板，演示图形运动的轨迹，帮助学生形成运动观念，不断研究中考优质题型，以中考题为依托开展课堂教学，注重对优秀考题的剖析、研究，关注解题策略，提高解题能力。

編辑 赵飞飞