II 晶型利福平在两种混合溶剂中溶解度的测定和关联

琚 祥, 陈 葵, 朱家文

(华东理工大学 化学工程研究所, 上海 200237)

1 前 言

利福平(rifampicin)，化学名3-[[(4-甲基-1-哌嗪基)亚氨基]甲基]-利福霉素，分子式C43H58N4O12，分子量为 822.97，是半合成利福霉素类抗生素的一种，临床上主要用于治疗肺结核和麻风病等[1]。因其具有广谱抗菌作用、毒副作用小、疗效高等特点，目前越来越多地制作为复合药剂应用于其他疾病的治疗，例如心内膜炎、耐药性伤寒和呼吸道感染等，市场需求稳中有升，因此利福平生产技术和质量的进步具有现实意义[2]。

利福平复杂的分子结构使得其存在多种晶型及溶剂化物，与结晶系统使用的溶剂密切相关[3]。利福平的药用晶型为I 和II 晶型，I 晶型在正丁醇中重结晶获得[4]，II 晶型在丙酮中重结晶获得[5]。两种晶型在堆密度、溶出速率、粒径、热稳定性等方面有所不同，在一定条件下可以发生溶剂介导转晶和固体转晶相互转化。在工业生产中，无论采用正丁醇还是丙酮作为结晶溶剂，体系中都残留有前端工序带来的正丁醇溶剂组分，且在丙酮中结晶时，为追求大粒径产品，而添加少量水，因此都不能得到形貌完整的I 或II 晶型晶体，常是以混晶形式存在。而相关研究往往只关注了两种晶型在纯溶剂中的热力学数据，并未探究在溶剂中长时间平衡过程中利福平晶型的转变[6]，以及混合溶剂组成中的热力学数据。

本文研究I 晶型利福平在常用结晶溶剂中溶解时发生的晶型转变。系统测定在不同温度下II 晶型利福平在正丁醇-丙酮和水-丙酮两种混合溶剂体系中的溶解度，并采用多种经验方程对溶解度数据进行拟合。研究结果能够为利福平生产工艺优化和产品质量控制提供基础数据。

2 实验部分

2.1 试剂与仪器

I 晶型和II 晶型利福平，上海新铂化学技术有限公司，经高效液相色谱仪检测，纯度98.030%。经粉末X 射线衍射法(powder X-ray diffraction，PXRD)检测，结果如图1 所示，在13.6° 和14.4° 检测到I晶型的特征峰，在9.9° 和11.1° 检测到II 晶型的特征峰，原料分别为I 晶型和II 晶型利福平[7]。正丁醇、丙酮均为分析纯，由上海泰坦科技股份有限公司提供；去离子水，实验室自制。

BSA224S-CW 型分析天平(精度(±0.000 1) g)，赛多利斯科学仪器有限公司；DC-3015 低温恒温槽(精度 ±0.1 ℃)，上海恒平科学仪器有限公司；DZF-6020 型真空干燥箱，上海精宏实验设备有限公司；D8 Advance 型X 射线衍射仪，布鲁克(北京)科技有限公司。

图1 I 和II 晶型利福平的PXRD 特征图Fig.1 PXRD pattern of rifampicin I and II

图2 溶解度测定实验装置Fig.2 Schematic diagram of the experimental setup for solubility measurements

2.2 实验方法

实验所用装置如图2 所示。将过量I 晶型利福平分别加入到正丁醇、丙酮、正丁醇-丙酮、水-丙酮混合溶剂中，在一定温度下恒温搅拌6 h 以上，然后取底层沉淀做PXRD 分析，确定晶型是否发生转变。

测量溶解度数据的方法有平衡法[8-10]和动态法[11]，本文采取平衡法。将适量溶剂加入到玻璃夹套瓶中，打开恒温水浴槽并调节至指定温度，然后用精度为0.1 K 的温度计测量夹套瓶内体系温度，微调水浴槽温度，直至被测体系达到指定温度。当温度稳定后，加入过量的II 晶型利福平，搅拌6 h 使夹套瓶内溶液达到固液平衡。关闭搅拌，在该温度下静置6 h 以上，以保证固液分离，上层溶液中没有悬浮颗粒。然后吸取上层清液，并通过0.45 µm 微滤膜过滤至洁净已称重的培养皿中，迅速称量培养皿和溶液的质量。将培养皿放入真空干燥箱中，干燥48 h 以上，直至质量不再变化。

利福平在纯溶剂中的摩尔溶解度使用下式计算：

利福平在正丁醇-丙酮、水-丙酮混合溶剂中的摩尔溶解度使用下式计算：

其中，m1为溶质的质量(g)；m2和m3为不同溶剂的质量(g)；M1、M2和M3分别为溶质和不同溶剂的相对分子质量(g·mol-1)。

为确保溶解度测试数据的可靠性，实验时分别于搅拌4、6 和12 h 后取样分析，发现4 h 后溶液浓度已经稳定不变，因此搅拌时间6 h 足够保证固液溶解平衡。实验使用的溶剂易挥发，在实验装置上添加冷凝管，以保证溶剂的冷凝回流。每次实验重复3 次以保证数据准确性。对底层晶体过滤、烘干后，使用PXRD 检测，发现在实验过程中II 晶型利福平没有发生晶型转变。

为验证实验装置的可靠性，测量了不同温度下氯化钾在水中的溶解度，并将测量值与文献数据[12]比较，相对偏差在0.5% 以内，说明实验装置与方法是可靠的，可用于II 晶型利福平溶解度的测定。

3 实验结果与分析

3.1 I 晶型利福平在溶剂中的晶型转变

研究I 晶型在溶剂中的溶解度时，分析底物晶体的PXRD，如图3 所示。发现在正丁醇、丙酮、正丁醇-丙酮、水-丙酮溶剂中均发生了溶剂介导转晶，利福平从I 晶型转变为II 晶型。在I晶型溶解平衡过程中，逐渐形成II 晶型的晶核，然后晶体生长消耗了溶液浓度，进而又促进原先 I 晶型的溶解，这种晶型转变过程在一些多晶型药物中普遍存在[13]。所以不宜使用平衡法测量I 晶型利福平在上述溶剂中的溶解度数据。

图3 I 晶型利福平在不同溶剂中的PXRDFig.3 PXRD pattern of rifampicin form I in different solvents

3.2 II 晶型利福平溶解度数据的测定和关联

实验测量了在288.15～323.15 K 时II 晶型利福平在正丁醇-丙酮、水-丙酮混合溶剂中的溶解度，结果见表1 和2。

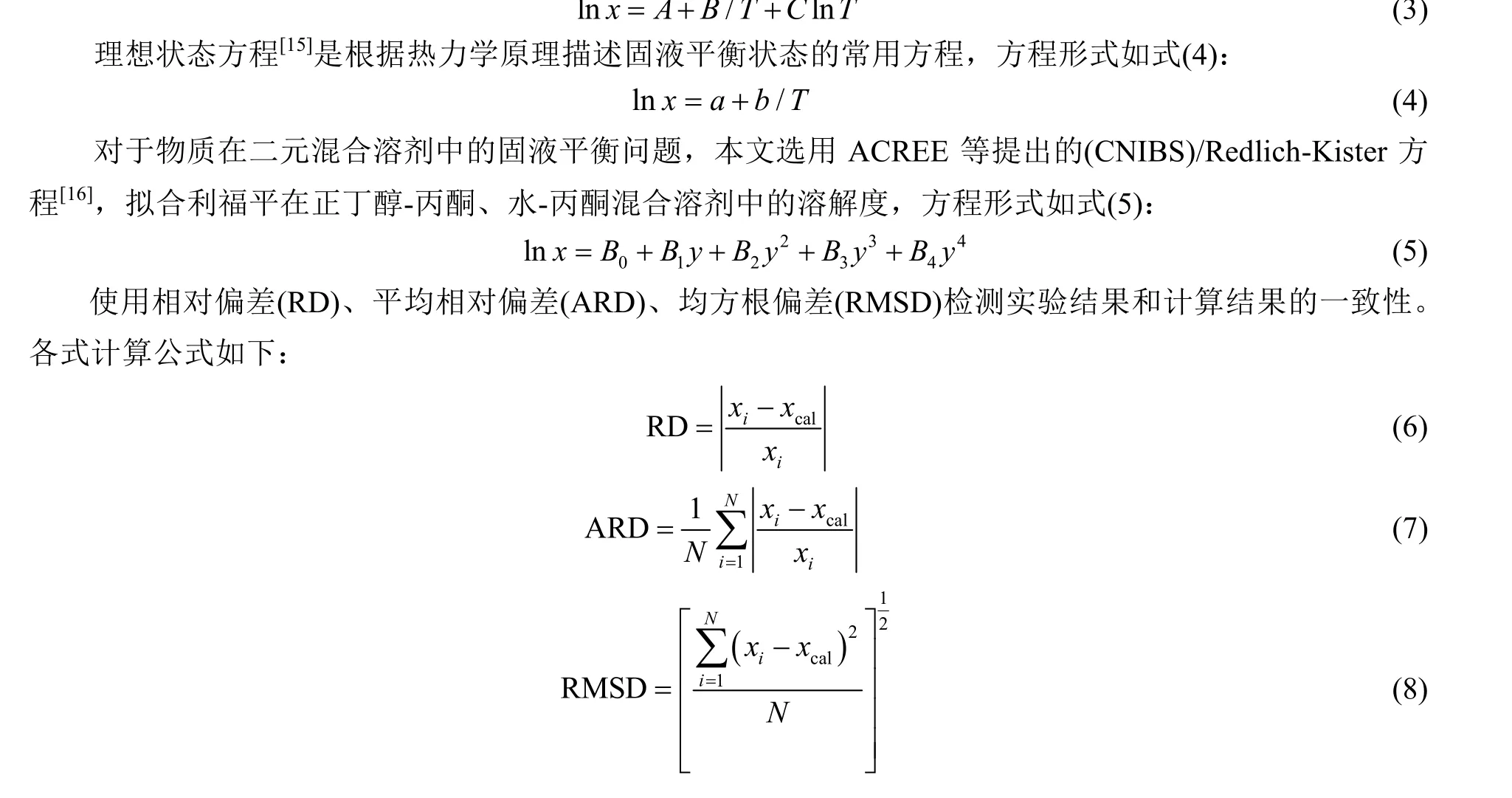
Apelblat 方程[14]越来越多用于溶解度数据的拟合，该模型假定溶液的焓变为温度的线性函数，经进一步简化、修订后可用于关联溶解度与温度之间的关系，方程形式如式(3)：

II 晶型利福平在不同配比的正丁醇-丙酮混合溶剂中的溶解度数据及不同模型计算值如表1 和图4 所示。从图中可以发现，利福平在不同配比的溶剂中，溶解度都随着温度升高而增大。当y1= 1.000 时，即溶剂为正丁醇时，利福平的溶解度最小。当y1= 0.350 时，利福平的溶解度最大。从图5 可以发现，在相同温度下，随着混合溶剂中正丁醇含量的增加，利福平的溶解度先迅速增大，达到最大值后，然后下降。这种变化趋势在高温时显著。低温时整体溶解度较低，变化不明显。其原因可能与分子间氢键有关，丙酮分子中存在羰基，形成氢键时羰基可作为氢键受体，但是分子内不存在氢键供体，在纯丙酮溶剂中，不形成氢键，所以丙酮易挥发，且黏度小。正丁醇分子中存在一个羟基，形成氢键时，既能作为氢键受体又能作为氢键供体，正丁醇分子间可以形成氢键，所以正丁醇相对丙酮挥发性小，黏度大。利福平分子结构复杂，分子内存在羟基、胺基、羰基等多种能形成氢键的基团。在丙酮中加入正丁醇，正丁醇中的羟基与利福平分子间形成氢键，使得溶解度增大。但当正丁醇含量增加，由于正丁醇分子间的氢键数量增加，使得利福平与正丁醇形成氢键减少，导致溶解度下降。

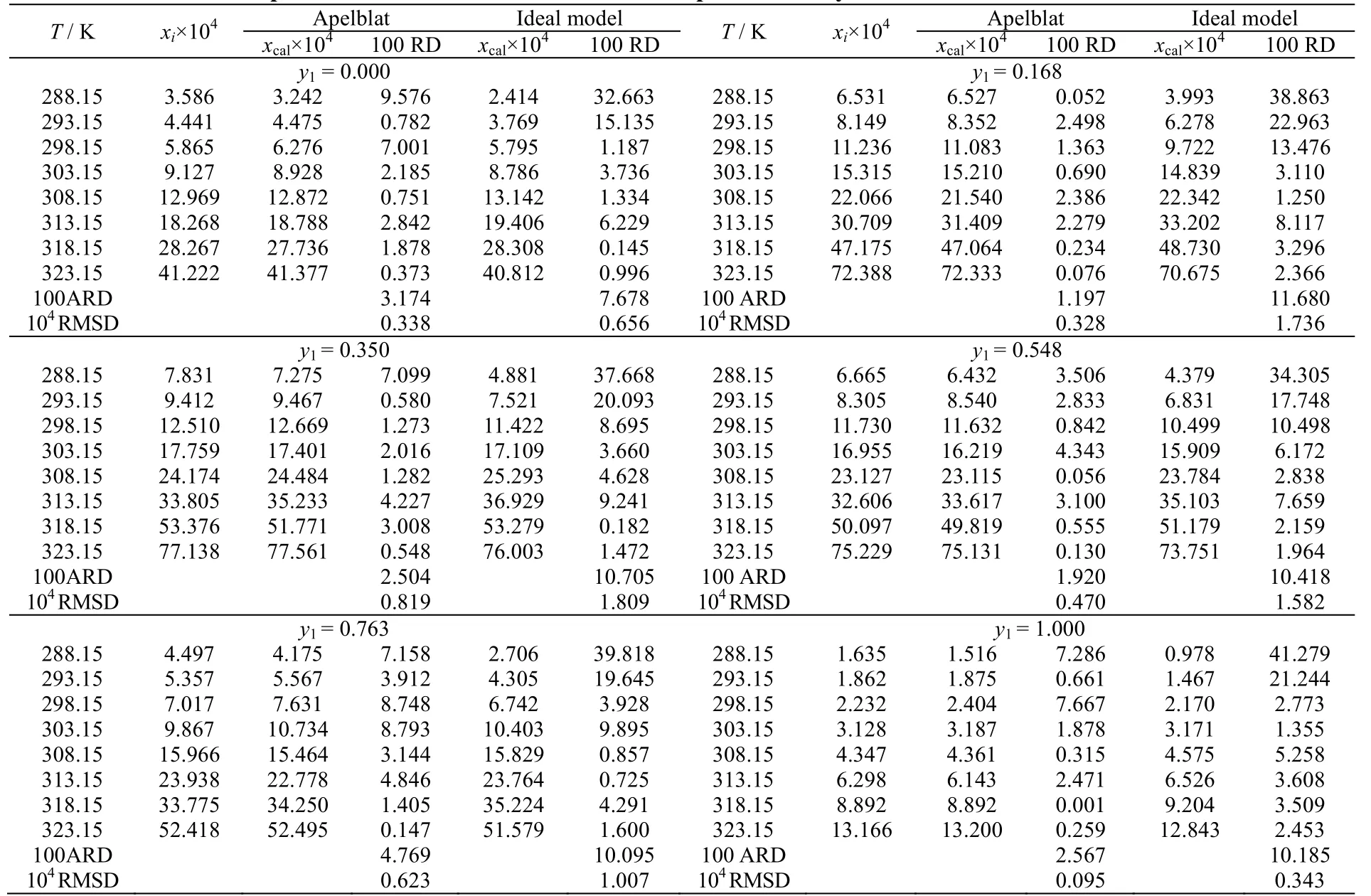
表1 利福平在正丁醇-丙酮混合溶剂中的溶解度实验值与计算值 Table 1 Experimental and calculated values of rifampicin solubility in 1-butanol-acetone mixed solvents

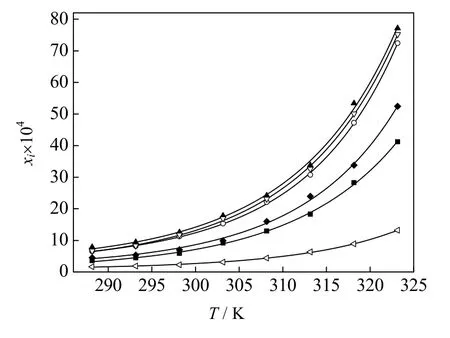
图4 利福平在正丁醇-丙酮混合溶剂中 的溶解度 Fig.4 Solubility of rifampicin in 1-butanol-acetone mixed solvents

图5 利福平在正丁醇-丙酮混合溶剂中的溶解度 与溶剂组成关系 Fig.5 Relationship between solubility of rifampicin in 1-butanol-acetone mixed solvents and composition of solvents

II 晶型利福平在不同配比的水-丙酮混合溶剂中的溶解度数据及不同模型计算值如表2 和图6 所示。从图中可以发现，利福平在不同配比溶剂中的溶解度随着温度升高而增大。从图7 可以发现，在同一温度下溶解度随着混合溶剂中水含量的增大而增大。其原因应该与正丁醇-丙酮体系类似，容易形成氢键的水分子，使得溶剂中与利福平形成的氢键增加，进而使得溶解度增大。

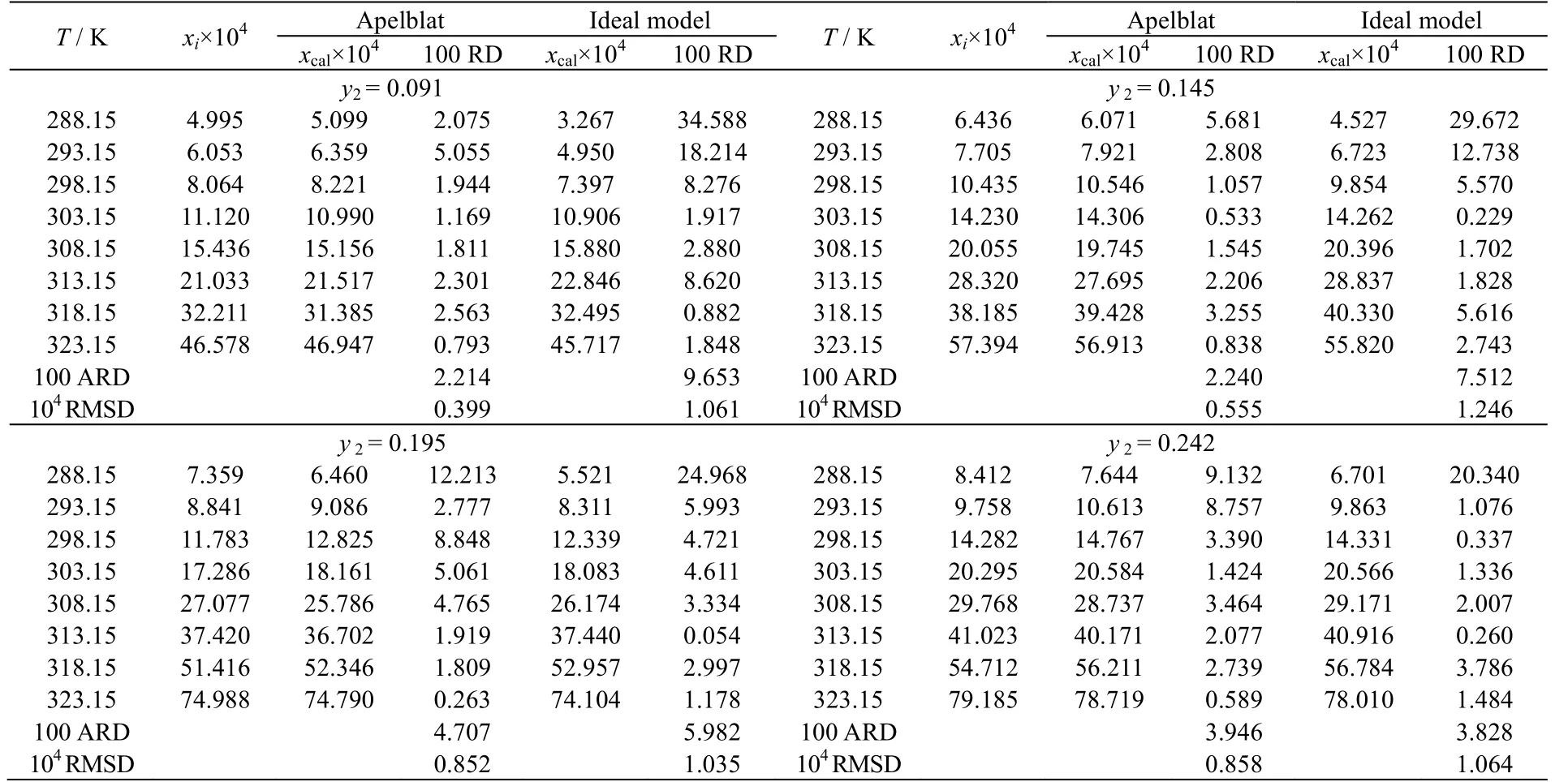
表2 利福平在水-丙酮混合溶剂中的溶解度实验值与计算值Table 2 Experimental and calculated values of rifampicin solubility in water-acetone mixed solvents

图6 利福平在水-丙酮混合溶剂中的溶解度Fig.6 Solubility of rifampicin in water-acetone mixed solvents

图7 利福平在水-丙酮混合溶剂中的溶解度与溶剂组成关系Fig.7 Relationship between solubility of rifampicin in water-acetone mixed solvents and composition of solvents

分别采用Apelblat 方程和理想状态方程拟合两个溶剂体系中的实验数据，结果见表3。在正丁醇-丙酮溶剂中，两个方程的拟合R2均大于0.993，ARD 分别小于5%、12%，最大RMSD 分别为0.819×10-4和1.809×10-4，从整体结果上来看，Apelblat 方程的拟合效果要优于理想状态方程。(CNIBS)/ Redlich-Kister方程的拟合结果见表4，R2大于0.994，关联良好。在水-丙酮溶剂中，Apelblat 方程和理想状态方程的拟合 R2均大于 0.994，ARD 分别小于 5%、10%，最大 RMSD 分别为 0.858×10-4和 1.246×10-4，同样 Apelblat方程的拟合效果优于理想状态方程。(CNIBS)/Redlich-Kister 方程的拟合R2大于0.999，关联良好。

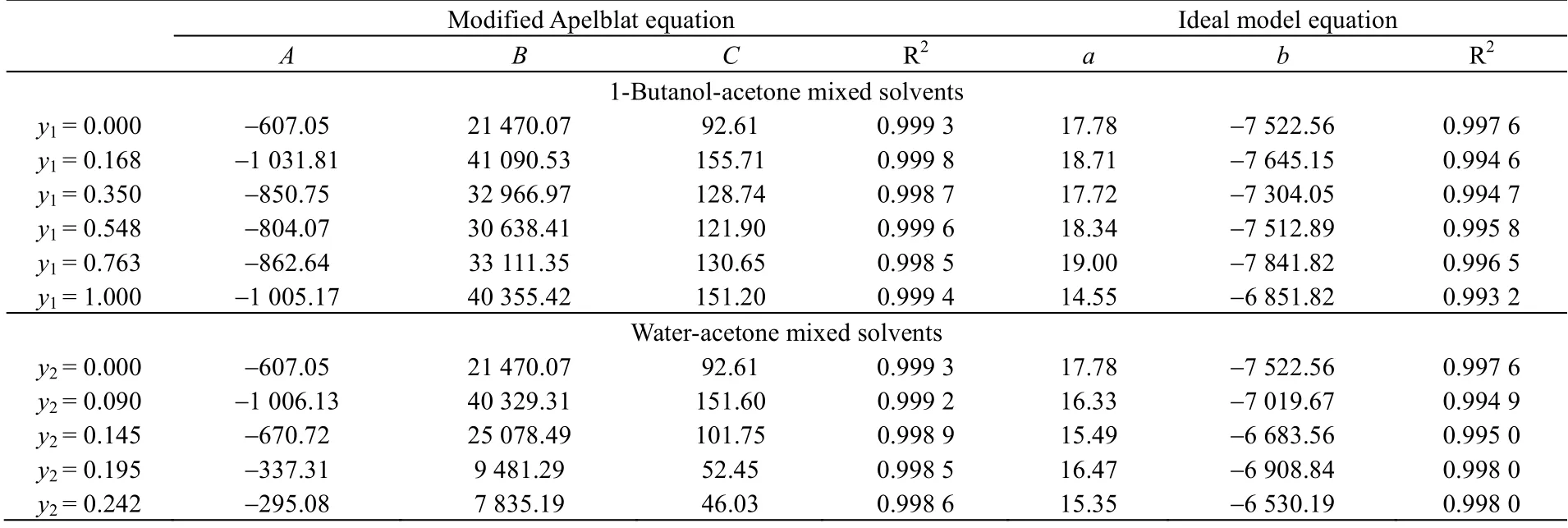
表3 Apelblat 方程和理想状态方程模型参数回归结果Table 3 Parameters of the Apelblat equation and ideal model

表4 (CNIBS)/Redlich-Kister 方程模型参数回归结果Table 4 Parameters of the (CNIBS)/Redlich-Kister equation and ideal model

3.3 热力学参数

固液平衡体系的热力学参数可以通过修正的van’t Hoff 方程来计算。在恒定压力下溶质的标准摩尔溶解焓计算公式如式(9)[17]：

其中Tm为所有实验温度的平均值(本实验中Tm= 305.22 K)，计算公式如式(10)：

式中：N 为实验数据的温度点数。

标准摩尔溶解吉布斯自由能和标准摩尔溶解熵计算公式如式(11)、(12)：

式中：intercept 是以lnxi和(1/T −1/Tm)作图得出的截距。

溶解过程中焓变和熵变的贡献通过式(13)、(14)计算：

两种混合体系中的热力学计算结果如表5 所示。在两种体系中利福平和均为正值，表明在这些体系的溶解为吸热过程，该结果与溶解度随着温度升高而增大相符合。此外根据van’t Hoff 方程计算得到的吉布斯自由能为标准状态下的溶解吉布斯自由能，所以不能据此判断反应是否自发进行。ξH的计算结果均大于50%，说明在实验过程中ΔsolHom对ΔsolGom的贡献较大。

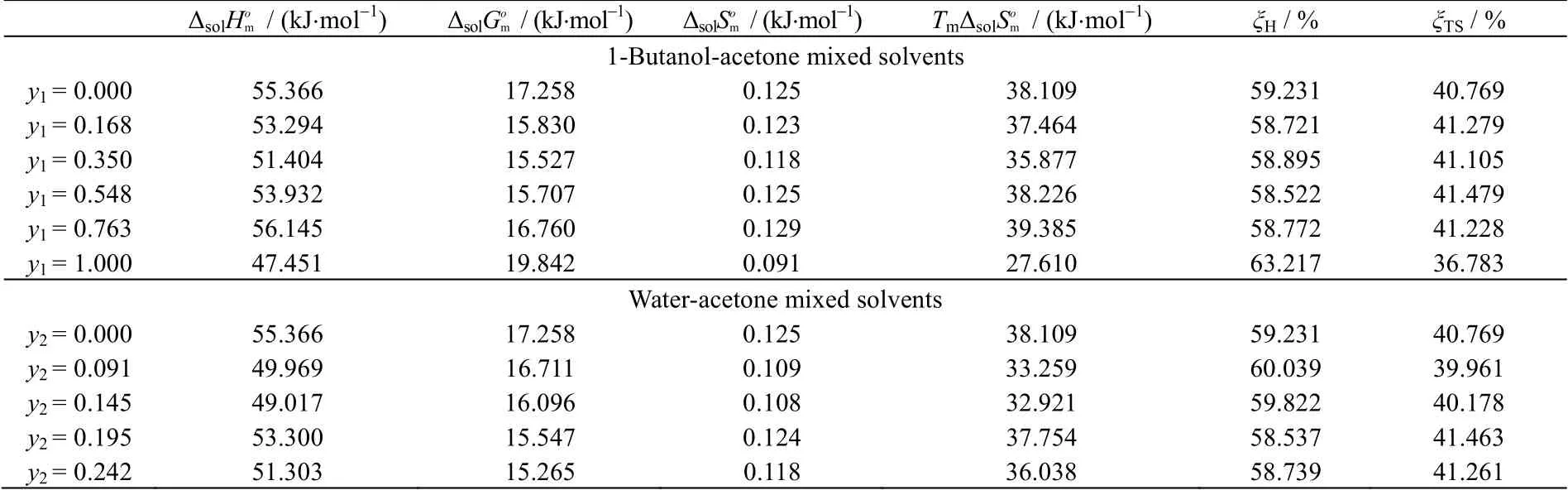
表5 利福平溶解热力学性质Table 5 Thermodynamic properties of rifampicin solutions

4 结 论

(1) I 晶型利福平在正丁醇、丙酮、正丁醇-丙酮、水-丙酮混合溶剂中发生溶剂介导转晶，转变为II晶型，因此在这些溶剂中I 晶型的溶解度难以通过平衡法测量。

(2) 采用平衡法测定了288.15～323.15 K 时II 晶型利福平在正丁醇-丙酮和水-丙酮混合溶剂体系中的溶解度。在所有体系中，溶解度随着温度升高而增大。使用Apelblat 模型能够很好拟合溶解度数据，关联结果良好。

(3) 在正丁醇-丙酮体系中溶解度随着正丁醇的摩尔比增加先增大后减小，在摩尔比0.350 附近溶解度最大。在水-丙酮体系中，溶解度随着水的摩尔比增加而增大。引入温度参数采用(CNIBS)/Redlich-Kister模型进行修正，结果显示关联良好，改善了模型单因素预测的缺陷，有效地提高了利福平在二元混合溶剂中溶解度的预测精度。

(4) 根据van’t Hoff 方程计算了利福平在两种混合溶剂中的ΔsolHom、ΔsolGom和ΔsolSom。由结果可知，ΔsolHom均为正值，表明利福平在溶剂体系中的溶解均为吸热反应，溶解度值随着温度升高增大，实验值很好地符合这一结论。

符号说明：

a,b — 理想状态方程模型参数

A,B,C — 修订的Apelblat 方程参数

ARD — 平均相对偏差

B0,B1,B2,B3,B4— 模型(CNIBS)/R-K 方程参数

m1,m2,m3— 溶质利福平和溶剂的质量，g

M1M2M3— 溶质利福平和溶剂的相对分子质量，g·mol-1

R — 气体常数，J·mol-1·K-1

R2— 拟合优度判定系数

RD — 相对偏差

RMSD — 均方根偏差

T — 实验温度，K

Tm— 平均温度，K

xcal— 溶质摩尔分数的计算值

xi— 溶质摩尔分数的实验值

y1— 正丁醇-丙酮溶剂中正丁醇的摩尔分数，%

y2— 水-丙酮溶剂中水的摩尔分数，%