基于OVAC的IPC和励磁作用提高暂态稳定研究
2020-08-07王俊岩
常 升,王俊岩,孙 欣
(东北电力大学,吉林 吉林 132012)
目前,随着不断促进区域电网的互联,其规模逐渐增大,电力系统在远距离传输线路的运行环境显得非常严峻,电网的稳定性问题变得更加突出。灵活交流输电系统(FACTS)中的相间功率控制器在提高系统暂态稳定性方面具有一定的作用[1-2]。文献[3]提出了调谐型可控相间功率控制器(TCIPC),在系统发生大干扰时具有良好的阻尼特性,起到提高暂态稳定性的作用。文献[4]将相间功率控制器(IPC)进行了改进,建立了动态可控相间功率控制器(DCIPC),验证了带有DCIPC的控制器可以提高系统的暂态稳定性。励磁系统在维持电力系统及发电机端电压稳定以及提高同步发电机并列运行方面具有重要。文献[5]说明了发电机励磁模型和参数对提高电力系统的稳定性有很大影响。文献[6]提出了对于长距离线路输电的发电机采用装电力系统稳定器(PSS)的高增益,高响应励磁系统有利于提高电力系统稳定,在传输水平较高的电力系统中,当发生故障时,系统仅通过励磁装置来调节其稳定性是难以调控的。
FACTS器件在近年来发展迅速,IPC就是新型器件之一。IPC相对于TCSC或者SVC器件更有优势,其优势在于通过调节IPC中的移相器、电感和电容,可以起到抑制短路电流和电压解耦的优良特性[7]。国外IPC已在实际工程中发挥作用;国内IPC对提高暂态稳定也取得了一些成果,因此,本文将IPC与励磁控制结合在一起,采用最优变目标控制策略,设计相应的控制器规律,提高系统的暂态稳定。
1 带有TCIPC的单机系统数学模型
1.1 系统接线
将传统的相间功率控制器模型进行电力电子技术改造可以形成可控相间功率控制器。可控相间功率控制器由两条支路构成,并且都由晶闸管触发控制。改进后的电感支路,可以等效成TCR,若要改变该支路的感抗值的大小,调节该支路上的触发延迟角的值即可完成;改进后的电容支路,可以等效成TCSC,可以实现该支路容抗的调节。
装有可控相间功率控制器(TCIPC)的单机无穷大系统见图1,其中:E′g为发电机暂态电势;δ为发电机功角;X为输电线路和变压器电抗总和;φ1和φ2分别为IPC电感与电容支路等效移相角;XL、XC分别为感性和容性电抗;U为无限大容量系统母线电压。
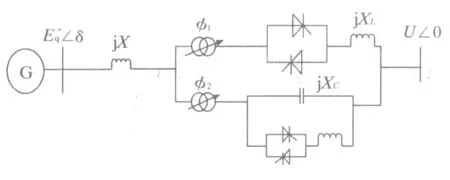
图1 装有TCIPC的单机无穷大系统
1.2 计及励磁作用的发电机模型
研究图1中系统暂态稳定性,发电机采用三阶模型,考虑发电机的励磁调节,其模型如下:
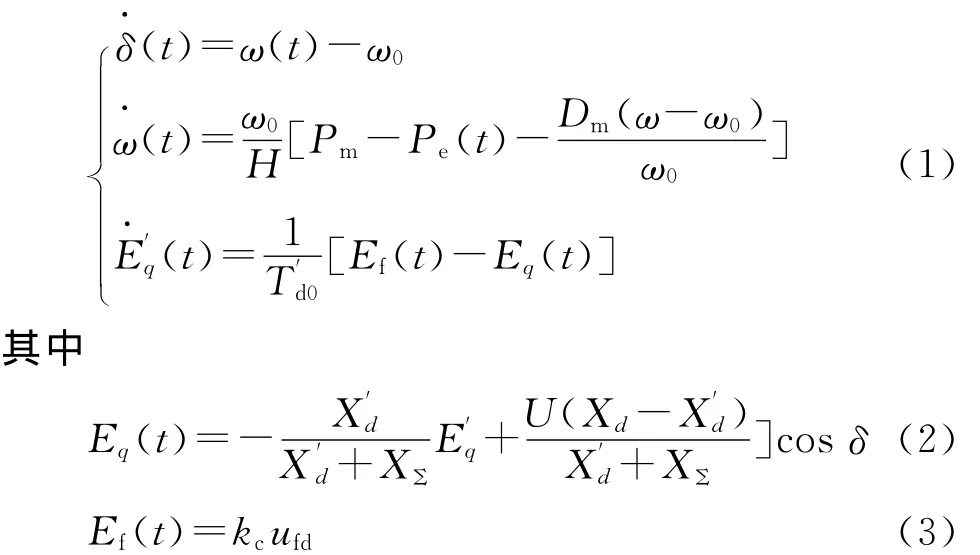
式中:ω是角速度;ω0是额定角速度;Pm是发电机机械功率;Pe是发电机电磁功率;Dm是阻尼系数;H是惯性时间常数;E′q是发电机q轴暂态电动势;Eq是q轴空载电动势;Ef是强制空载电动势;ufd是发电机励磁控制;T′d0是励磁绕组时间常数;Xd和X′d分别为发电机直轴电抗和暂态电抗,XΣ=X+XL∥(XC∥XL);kc是自动电压调节器的放大倍数。
1.3 TCIPC功率控制模型
式(1)中输电线电磁功率与TCIPC的移相电压、电感和电容的等效电抗均有关,本文先从简单情况入手,针对调谐型TCIPC模型进行分析,得出其传输功率为:

1.4 带TCIPC的单机系统模型
发电机采用三阶模型,TCIPC中的TCR支路与TCSC支路可以利用成一阶惯性环节来等效其动态过程[8-9],从而得出单机远距离输电系统模型如下:
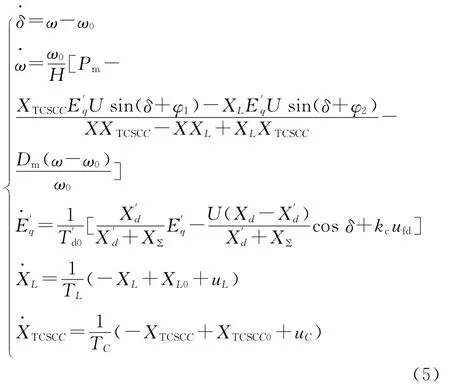
式中:uL为 TCIPC电感支路的控制量;uC为TCIPC电容支路的控制量;TL与TC分别为为TCR支路和TCSC支路控制器的时间常数;XL为TCR中电感支路电抗,XL0为TCR中可调电感的初始电抗值;XTCSCC为TCSC中电容支路电抗;XTCSCC0为TCSC中可调电容的初始电抗值。
2 计及励磁和IPC作用的最优变协调控制策略
电力系统属于非线性系统,大多数控制理论通常是将电力系统的非线性方程进行线性化。这些理论得出的数学模型不够精确,通过数学模型得出的控制规律也达不到理想的控制效果,在此基础上设计的控制器也很难适应大干扰情况。但最优目标控制理论,不需要将非线性系统线性化,而是直接采用非线性系统原来的模型,使得其在最大程度上保持原来非线性系统的特性,因此,本文的采用最优变目标控制策略对1节中建立的模型进行协调控制。
一般的控制策略是使系统直接驱动到其稳定平衡点,但是,对于像电力系统这样的复杂系统,会存在多个稳定平衡点。在故障切除时,若系统状态在最大稳定域以外,那么系统不会回到该周期的稳定平衡点,而是会运行到后续某一周期的稳定平衡点。如果仍试图驱动到该周期的稳定平衡点就不会达到
对应最大励磁电压下的发电机交轴电势,XLmax和XCmax为IPC的XL和XC最大值,此时,系统有最大的暂态稳定域;在滑差过零后,则取故障后系统稳定平衡点的值[13]可选为:理想的控制效果。
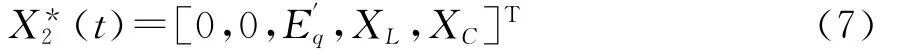
本文借助文献[9]提出的最优变目标控制策略,解决了最优目标控制的不足。最优变目标控制策略首先驱动到系统按照最大能量耗散、最大稳定域的人工中间平衡点,再驱动到故障后的稳定平衡点,因此,E′*q、X′*L、X*C在滑差过零前,取相应人工中间稳定平衡点的值,可以选择平衡点的值[10-12]为:
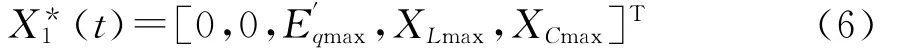
3 仿真研究
本文使用MATLAB/SIMULINK仿真软件对图2的单机无穷大系统进行仿真,励磁采用PI控制、励磁与TCIPC采用PI控制以及TCIPC和励磁采用最优变目标控制进行比较,验证IPC的对暂态稳定作用以及最优变目标控制策略的有效性。
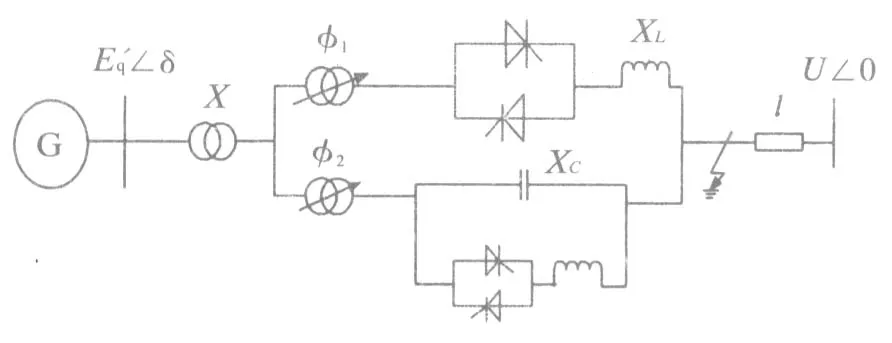
图2 简化单机无穷大系统仿真图
系统参数选取如下[5,12]。
a.单机无穷大系统:D=5.0,H=7.45p.u.,Xd=1.79p.u.,Xq=1.71p.u.,X′d=0.17p.u.,T′d0=4.1s,Xt=0.51p.u.,Xl=0.41p.u.。
b.IPC 参数大小:移相角φ1=-120°,φ2=120°,TC=0.015s,TL=0.015s。
PI参数选取:Ka=70,Ta=0.000 1。
仿真条件:仿真时间20s,在10s发生三相短路故障,故障持续时间0.2s。
发电机功角对比曲线见图3。由图3可以看出,系统未加TCIPC控制器时系统功角的控制曲线波动范围最大,振荡持续时间最长;加了TCIPC控制器后,振荡幅度是52.3°,振荡时间较长,10s后达到稳定;在故障发生后,采用最优变目标控制时,振荡幅度明显缩短,其振幅最高为52.2°,3s后功角恢复到δ=39.8°,系统达到稳定状态。可以看出,最优变目标控制能很好地改善系统暂态稳定。

图3 发电机功角对比曲线
线路传输功率对比曲线见图4。由图4可知,系统未加TCIPC控制器时的线路传输功率振荡曲线开始振荡幅度稍小一些,但是后期振荡时间最长,振幅也比较明显;加了TCIPC控制器后,其最高振幅是1.09p.u.,振荡时间较长;采用最优变目标控制时,其振幅最高为1.08p.u.,振幅明显减小,2.3s后恢复稳定。
发电机转子角速度对比曲线见图5。由图5可知,系统未加TCIPC控制器时的发电机转子角速度振荡曲线在故障切除之后振荡幅度范围最大,振荡时间最长;加了TCIPC控制器后,振荡时间较长,经过10s后,波形趋于稳定;在采用最优变目标控制时,振荡次数明显减少,3s后恢复稳定。
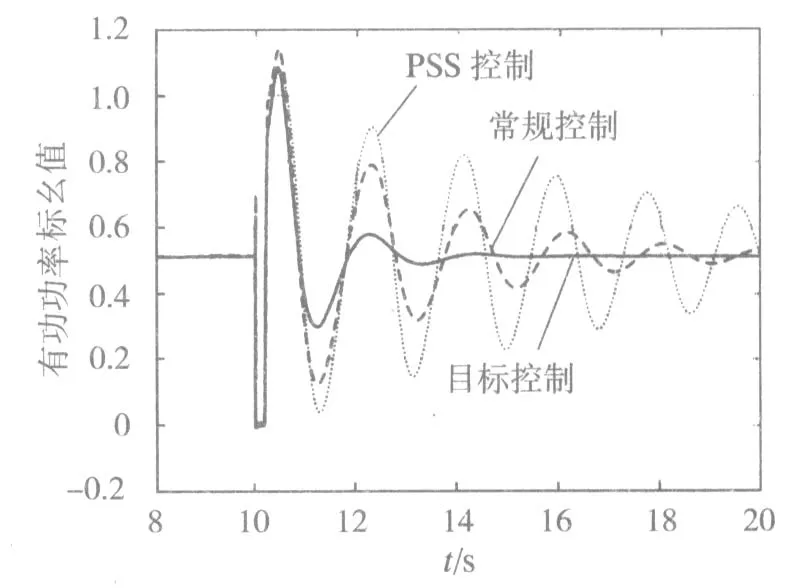
图4 线路传输功率对比曲线
发电机端电压对比曲线见图6。由图6可知,系统未加TCIPC控制器时,发电机端电压振荡曲线振荡幅度最大,振荡时间也最长;加了TCIPC控制器后,其振荡最高幅值1.04p.u.,振荡幅度很大,经过7s后趋于稳定;在最优变目标控制下,其振荡最高幅值为0.93p.u.,振荡次数明显减少,经过2.3s后振幅趋于稳定。通过对比可知,最优变目标控制可以有效抑制振荡,提高暂态稳定。
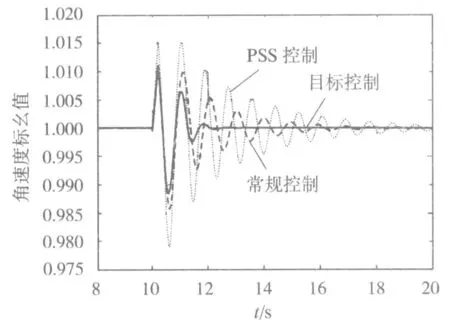
图5 发电机转子角速度对比曲线
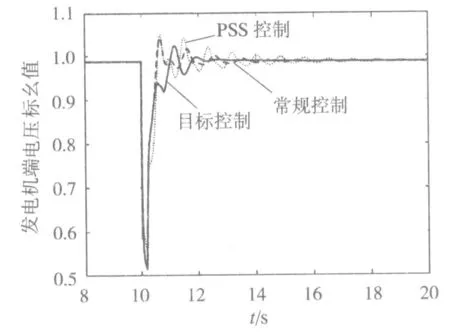
图6 发电机端电压对比曲线
4 结论
本文建立了包含励磁和IPC控制参数的简单系统暂态稳定分析状态方程,通过IPC传输功率表达式将IPC控制参数引入方程中,并基于最优变目标控制理论推导出计及励磁和IPC作用的协调控制策略。
采用的IPC和励磁系统最优变目标协调控制策略不需要将非线性系统线性化,保留了非线性系统的特性。仿真结果表明本文提出的控制策略可以有效提高系统的暂态稳定性。
