基于Weibull分布的测控装备寿命预测方法研究

金山

（91550部队41分队，辽宁 大连 116023）

武器试验定型离不开测控装备。靶场作为装备使用单位，更关心装备实际使用寿命，而装备研制方给出的设计寿命通常比较保守，实际使用寿命往往更长。过早判定装备报废，容易形成浪费，而一些长时间处于恶劣环境中的装备可能具有很高的故障概率。靶场武器试验，准备实施周期长，若期间测控装备出现故障，将影响试验进度，浪费人力物力[1]。利用寿命预测技术定期对参试装备的状态进行评估，可挖掘装备潜在使用价值，降低出现故障的风险，为装备的更新维护提供参考依据。

由于寿命预测技术在工程应用中的巨大价值，国家中长期规划（2006—2020年）将其列为重要研究方向。国内外研究人员在理论上和试验上，从单一材料到复杂设备，开展了一系列深入、系统的分析，形成了多种预测方法。例如文献[2]使用基于 AMSAA和 MTBF-T模型评估电子设备使用寿命。文献[3]总结归纳了寿命预测技术在机械装备领域的研究情况。文献[4]提出基于支持向量回归的方法用于现代气象雷达寿命预测。每种方法的适用性不同，应用场景也不同。测控装备组件数量多，构成复杂，文中将对寿命预测方法在测控装备中的应用进行具体分析。

1 寿命预测技术和方法

1.1 寿命预测技术基本概况

寿命预测是指在规定的运行环境下，可确保设备安全、经济运行的剩余时间。它被定义为条件随机变量：

式中：tr为设备/材料的剩余运行时间；t′为失效时间的随机变量；t为机器的当前工作时长；Z(t)为当前时刻之前的有关该设备/材料的所有历史使用情况[5]。

寿命预测可分为早期预测和中后期预测。早期预测的目的是确定设备的设计寿命或计算寿命，主要以理论和试验的方法进行。中后期预测是从装备接收（交付）开始到最终报废退出使用全过程中，为了避免设备运行期间出现意外事故，监测设备状态，分析设备的当前和历史运行状况，评估保证设备安全运行的剩余时间，达到剩余寿命预测的目的。

寿命预测的对象包括机械装备及各种零部件、光电子元器件和各种测试材料，其研究发展可追溯到19世纪末。德国Whler提出了著名的S-N疲劳寿命曲线及疲劳极限的概念，后经不断研究发展，形成了经典的疲劳强度理论，在工程中得到广泛的应用。此后随着金相显微镜在金属微观结构领域的应用，基于裂纹扩展规律的研究成为人们关注的焦点，用断裂力学的方法表达裂纹扩展规律的Paris公式等理论相继产生。进入到21世纪，温度和腐蚀等环境因素对寿命预测的综合影响逐渐融入到预测技术中，针对复杂环境对寿命影响的研究不断深入。人工神经网络、专家系统等新兴算法在寿命预测领域应用也取得了一定的进展。

1.2 常用的寿命预测方法

目前关于产品寿命预测的方法可分为“白箱”方法和“黑箱”方法两大类[6]。“白箱”方法即基于失效物理的方法，是以产品失效机理为基础，通过建模分析，从产品的物理、化学等微观结构角度出发，分析性能下降过程，明确产品发生故障的本质、规律和原因，以便对产品进行有针对性的改进。退化轨迹理论就是一种典型的“白箱”方法。不同产品器件的退化轨迹曲线不同，当存在n个样本时，对应有n条退化轨迹。用于表征产品性能退化轨迹的数学模型主要有以下4种[7]：

式（2）—（5）中：αi、βi为未知参数；yi为第i个产品实际性能退化量；i为受试样本数；t为测试时间。试验过程中，利用收集到的产品性能退化数据，采用极大似然法来估计退化轨迹中αi、βi的值，由此建立产品退化轨迹模型，得到产品在实际条件下的寿命分布。

该方法的具体预测步骤如图1所示：

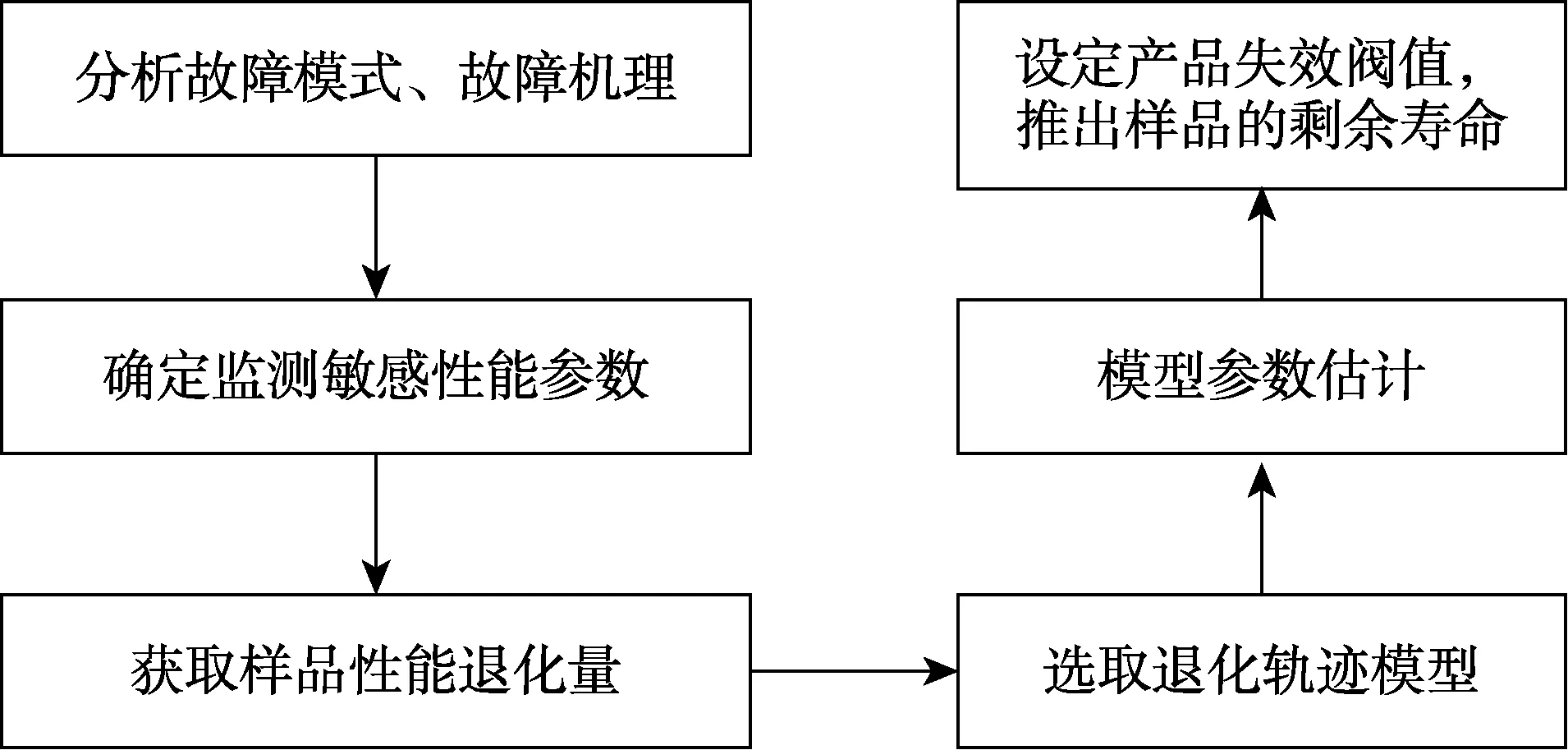
图1 基于退化轨迹的寿命预测方法预测步骤Fig.1 Prediction steps of life prediction method based on degradation trajectory

“黑箱”方法即基于数据驱动的方法，是一种依赖于数据的经验建模方法。通过对产品的失效时间进行统计，将其拟合成某种分布形式，利用失效数据确定各分布参数，进而进行可靠性评估和预测。“黑箱”方法中使用的典型分布有正太分布、Weibull 分布、指数分布、二项分布等。Weibull 分布由于适用性强而被广泛应用于各个领域。设x服从二参Weibull 分布，其概率密度函数和分布函数为：

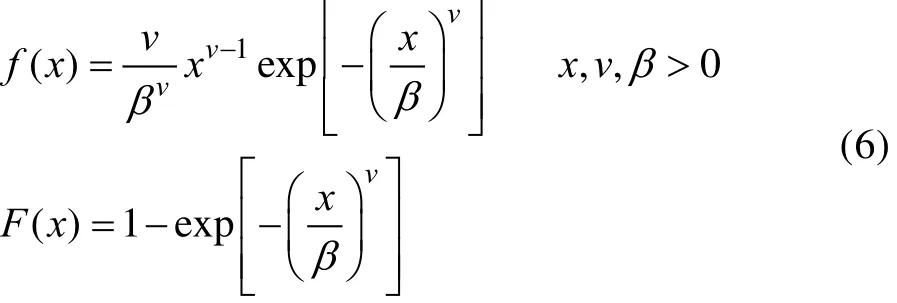
式中：v为形状参数；β为尺度参数。当v<1时，Weibull分布的值是递减的，适合于早期失效建模；当v>1时，Weibull分布的值是递增的，适合于磨损或老化失效建模；当v=1，Weibull分布就成了指数分布，适合于随机失效建模；当v≥3.5时，其曲线趋于正态分布的情况。因此，可以看出Weibull分布的适应范围更加广泛，可以更加准确地描述复杂系统的寿命特征。

2 测控装备寿命预测算法的选择

测控装备主要分为六大类：遥测装备、遥控装备、无线电跟踪测量装备、光学跟踪测量装备和通信装备等[8]。各部分共同担负起测控保障任务，整个系统构成复杂。不同部件的故障机理不同导致寿命分布不同，而整套装备的剩余寿命取决于系统内所有部件寿命的短板。在寿命管理过程中，一方面通过各传感器获取的测量参数反映装备中各部件或板卡的工作状态信息，通过这些散件的工作状态信息推测各分系统或整机的工作状态。文献[1]给出了某型脉冲雷达设备结构连接及各状态的对应关系，如图2所示。从图2中可以看出，整型装备由多个分系统构成，各分系统又由多个部件构成，系统结构复杂，针对不同型号的测控装备需要建立不同设备状态及结构网络，针对性较强。另一方面以各分系统或整机为单元，根据装备使用的历史数据，如工作时间、出现故障时间、故障原因等推测故障率在时间维度上出现的概率。采用“黑箱”方法，对各型装备均具有一定的适应性，但该方法在数据量上有一定的要求。

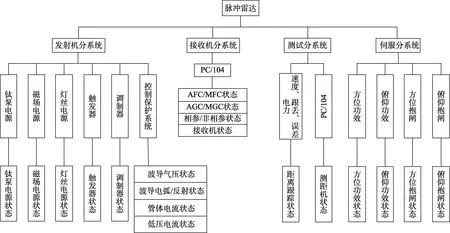
图2 脉冲雷达设备结构连接及各状态的对应关系Fig.2 Structure connection of pulse radar equipment and corresponding relationship of various states

结合测控装备种类繁多的特点，选择测控装备寿命预测算法时应考虑以下两点：测控装备构成复杂，涉及到的参数繁多，不同装备建立的性能衰变模型不同，且模型不易精确建立；测控装备在靶场使用过程中并不是频繁地发生故障，部分分系统或整机故障历史样本数据不足。

由1.2节可知，测控装备模块繁多，构成复杂，各模块组件失效机理不尽相同，整型装备的退化轨迹函数难以获得。基于数据驱动的寿命预测方法是不错的选择。由于样本个数有限，依靠大量数据进行推算的算法并不适用。通常认为，复杂的机电产品具有像电子产品一样服从指数分布的寿命分布函数。然而实践证明，复杂机电产品中只有小部分的寿命分布函数是服从指数分布的，大部分遵循Weibull分布。通过对Weibull分布的研究，指数分布只是其特殊形式[9]。因此，采用Weibull分布描述测控装备寿命分布函数更加合理、准确。

3 基于Weibull分布的测控装备寿命预测

对于二参数Weibull分布，只有在确定尺度参数和形状参数后，才能利用分布模型计算各可靠性指标。现有的两类常用参数估计方法为图解法和解析法：图解法简便易行，但主观因素影响大，参数估计精度较低；解析法精度较高，但计算量较大，算法复杂。

从预测精度考虑，解析法更好，虽然其算法计算量较大，但是借助于目前的数学软件和计算机强大的运算能力，这一问题已得到有效缓解。在解析法中，一般认为最大似然估计法精度最高[10]。因此，对二参Weibull分布进行参数估计时，采用最大似然估计法。

设系统寿命X服从二参Weibull分布，其故障分布函数为：

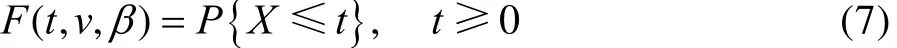
该分布表示故障发生在给定时间t或它以前的概率。测控装备寿命样本并非所有数据都是元件出现故障时获得的，还可能包含定时截尾样本。设样本共有N个数据，其中包含故障数据和结尾数据，此时最大似然函数为[11]：

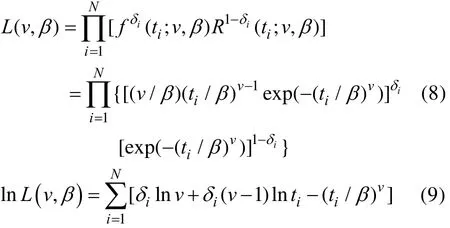
当 ti为故障时间时，δi=1；当 ti为截尾时间时，δi=0。

分别求解等式（9）中v、β参量偏导数等于0时的解，可得关于v、β的超越方程：

两个参数值可通过Newton-Raphon方法进行求解。

4 结语

测控装备的可靠性是保证试验任务成功的基本条件。利用装备寿命预测理论对装备的可靠性进行分析，能够为装备的维护更新提供科学的参考依据。通过分析测控装备特点，采用Weibull分布可完成测控装备的可靠性评估。Weibull分布的参数估计复杂度较大，后续应进一步探讨更为精简有效的参数估计方法。同时，测控装备在维护使用过程中应注意收集样本数据，提高样本数量，从而提高预测精度。