基于A＊算法的无人机路径规划研究及分析

罗汉杰，林义尚，周杰，沈桂英，倪虹

（杭州师范大学钱江学院，杭州310018）

0 引言

无人机的航行时间周期短，电能消耗过快并且在飞行也存在一些安全隐患。在飞行过程中，路径规划成为了关键技术[1]。此技术不仅可以节能同时也能提高无人机的安全性。常用的规划算法有迪杰斯特拉（Dijkstra）算法、BFS 算法以及A*算法都是一些典型的最有效路径算法。通过比对寻找到各个节点的最小代价节点，对其最小代价节点进行不断扩展，直至找到最终的目的节点。本文采用Malabar 软件搭建无人机三维，利用以A*算法，对杭州师范大学钱江学院其中一区域为无人机飞行环境进行模拟。

1 MALAB建模

利用MLTLAB 开发性与交互性强、操作简便的特点。通过UG 导出STL 格式的外形数据。其模型外形由不同的顶点组成小三角形面片，多个面片组合可以实现了无人机整体各种形状的曲面。其面片的数据均采用以下格式

通过读取模型的外形数据得出以下结果。图1 为路空两用无人机MATLAB 建模空间结果。

图1 路空两用无人机MATLAB建模图

本次无人机路径规划所采用的是路空两用无人机在传统无人机基础结构上改良具备轮动、爬楼与飞行模式。传统四旋翼无人机由于工艺与技术限制，其受外界如大风、地形等影响较大。本无人机在硬件设计方面，通过齿轮传动，实现旋翼桨距距离、角度与位置的自由变化。提高了无人机在楼巷、丛林等狭小涵道与大风环境中的稳定性。内置的无刷电机调整转速，完成爬升、降落、转向多姿态变换。在无人机控制硬件方面：采用模块化架构形式，搭载Arduino2560 微型控制板，通过数据传输模块、电机驱动模块、飞行控制模块、六轴运动模块、GPS 模块、电子罗盘、气压计七大部分组成[3]。GPS 与电子罗盘双位置传感器的设置，有效提高了飞行需求。其中USV 摄像头收集外界图像，OpenCV 完成数据处理，基于A*算法完成路径的规划[4]。可以应对复杂的环境。可折叠并且结构简单，重量适中的特点也使其易于携带。

2 栅格模型的建立

以杭州师范大学钱江学院地形为例，取学校其中的一个区域进行无人机的路径规划，区域包括A 教学楼、B 教学楼，C 教学楼、第二实验楼及图书馆等在的区域。采用自主设计的陆空两用无人机进行试验，无人机建模图如图1 所示，飞行模式时机架呈X 型模式，轴距为500 毫米，构建以60×60 格的栅格模型，一个格边长为10 米，灰色部分为障碍物所在位置（建筑）。飞行轨迹障碍栅格模型图若图二所示，以蓝点为出发点，红点为目的地。

图2 飞行轨迹障碍栅格模型图

3 A＊算法路径规划

3.1 A★算法原理

A*算法是一种重要的启发式算法，它主要是用于在最优路径选择上，可以在静态路网中求解出最短最有效的路径，而其算法通过定义满足一定的评估函数，估计各个节点的搜索代价，通过比对寻找到各个节点的最小代价节点，对其最小代价节点进行不断扩展，直至找到最终的目的节点[5]。其一般公示如公示（1）所示：

其中，f（n）是从初始状态到最终状态的总代价估计，即从起点到终点的最小代价估计总值，g（n）是在状态空间中从初始状态到状态n 的实际的代价，即消耗的实际代价，h（n）是从当前节点到目标节点的估计代价，一般体现的是启发式的信息，即启发函数。为了寻找到最短路径即最优解，其中的关键在于如何选择f（n）。[5]

该算法在最短路径选择搜索算法中一般分类为：直接搜索算法，启发式算法，静态图搜索算法。

3.2 利用A★算法模拟路径

对于无人机的路线图基本可以作为一个几何栅格模型图进行求解，当无人机在地图中的运动方向为正方向时，即正东、正西、正南、正北方向，可以选择曼哈顿距离作为估价函数，曼哈顿距离为两个节点之间的x轴方向和y轴方向上的距离，因此启发函数可以看作为公式（2）所示：

假设行一个网格的飞行距离为D，即曼哈顿距离为D，则h(n)如公式（3）所示：

其中，m为目前节点，g为目标节点。曼哈顿正方向运动距离如图3 曼哈顿正方向运动示意图所示。

图3 曼哈顿正方向运动示意图

当无人机在路网图中除了正方向运动外还进行对角线的运动时，可以选择对角线为新的股价函数[6]，即如公式（4）所示：

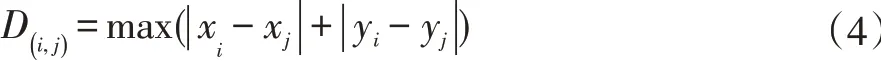
加入无人机的正向飞行和对角线飞行的距离都为D时，则启发式函数如公式（5）所示：

其中，m为目前节点，g为目标节点。如果对角线飞行的代价不为D而是时，因此需要计算，即沿着对角线移动的网格数为曼哈顿距离，然后将这两项合并为一项，所有的斜线都乘以D2，剩下所有正方向飞行距离都乘以D，即如公式（6-7）所示：

因此根性对角线函数如公式（8）所示：

曼哈顿对角线距离如图4 曼哈顿对角线距离示意图所示。

图4 曼哈顿对角线距离示意图

如果无人机在路网图中可以遵循任意角度移动时，此刻可以选择欧使用几里得距离进行估价距离运算，两点间的直线距离D将如公式（9）所示：

当直线距离和对角线距离代价都为D时，则h(n)启发函数如公式（10）所示：

由于欧几里得的正方先于曼哈顿距离正方向代价相同，而对角线距离代价比曼哈顿距离的对角线距离代价都小，所以使用欧几里得距离仍然可以得到最短的路径，但是会使得A*算法运行时间更久，因此可根据使用利弊进行随机选择欧几里得距离或者曼哈顿距离。

3.3 算法实现

在Python 环境下，构建一个模拟栅格图，障碍物通过随机生成模拟随机存在的障碍物，导入程序运行所需要的相关数据库如matplotlib，Rectangle，random_map，start，进行设置栅格大小，部分实现代码如下所示：

3.4 基于A★算法路径分析

通过使用曼哈顿距离代价进行A*算法估值运算[7]，无人机飞行距离如图5 飞行轨迹示意图所示。

图5 飞行轨迹示意图

由于在进行轨迹规划时使用的几何路网图进行求解最优解，因此并没有充分的考虑无人机的动力学和运动学，所以最后，必须要对最优轨迹进行平滑处理，以此满足现实状态下的无人机的机动转向性，形成最终的无人机飞行轨迹。

由于最优路线已通过A*算法进行计算出来，所以决定通过考虑无人机的最大法向过载，来引进圆弧化思想[2]，将无人机的运动轨迹进行平滑处理，利用公式（11）对目前最优路线进行平滑处理。

其中，ny.min代表无人机的最大法向过载，Vmin代表无人机的最小速度。

4 结语

本文针对静态目标区域进行分析规划，使用曼哈顿距离代价进行A*算法估值运算，计算出无人机最佳路径，但未考虑到无人机的运动学和无人机的安全性有待改善，总体来说此次的仿真模拟达到研究的目的，同时验证A*算法规划路径可行性和无人机的可飞性。