善用旧知,迁移新知,沟通关系,内化技能
2020-08-06曾庆欣
曾庆欣


六年级上学期数学教学的重头戏就是分数乘除法的解决问题。分数除法的解决问题历来是教师教学中的难点,更是学生学习中的难点。由于理解困难,学生往往靠记忆题型来解决问题,又或者有部分教师,在教学伊始就直接告知学生:“求比较量,用乘法;求单位‘1,用除法”的方法。这就失去了这种题型教学培养学生解决实际问题能力的作用。
本学期,我第一次执教六年级,毫无教学经验可言。而我又承担了执教《已知一个数的几分之几是多少,求这个数》这一内容的研究课教学任务。当时接到这节课任务的时候,我就开始犯难:究竟这节课的教学重难点是什么?如何去定位?查看网上的一些资料,这节课的课题按以前来说,应该叫“简单的分数除法应用题”。那是否只要学生判断出单位“1”已知,用乘法算;单位“1”未知,用除法算?又或者直接告诉学生,用“具体量÷对应的分率=单位“1””這个公式,让学生运用公式去解决问题就可以了呢?而至于为什么求“单位1”就可以用除法算?估计大部分学生是说不出原因的。可是,我翻看了一下教科书和教学用书,都只是呈现了列方程的方法,而一点都没有提到可以用除法计算。难道,我的教学里面,也只能呈现这种方法吗?
第一次试教的时候,我把分析关键句、找“单位1”作为重点,然后再通过例题的分析数量关系与旧知进行比较,从而掌握解决“已知一个数的几分之几是多少求这个数”的实际问题的方法。
【教学设计1】
一、谈话激趣,复习铺垫
1.下列各题中,应该把哪个量看做单位“1”?并找出题中的数量关系。
(1)爸爸的体重的■是小军的体重。
爸爸的体重×■=小军的体重
(2)故事书的本数占图书总数的■。
图书总数×■=故事书的本数
■■
2.师生交流
例题信息:根据测定,成人体内的水分约占体重的■,儿童体内的水分约占体重的■。
3.复习旧知
师:老师知道我们班的***体重就是35千克,你们能帮他算出他体内水分的质量吗?请同学们分析好数量关系,并列式解答。
(学生独立解答后汇报)
师:你是怎样算的?为什么用乘法算?你们在解决“小明体内水分质量”的时候,是把谁看做“单位1”?
电脑显示:儿童体内的水分约占体重的■
?kg 单位“1”
生回答后出示:儿童的体重×■=儿童体内水分的重量
35×■=28(千克)
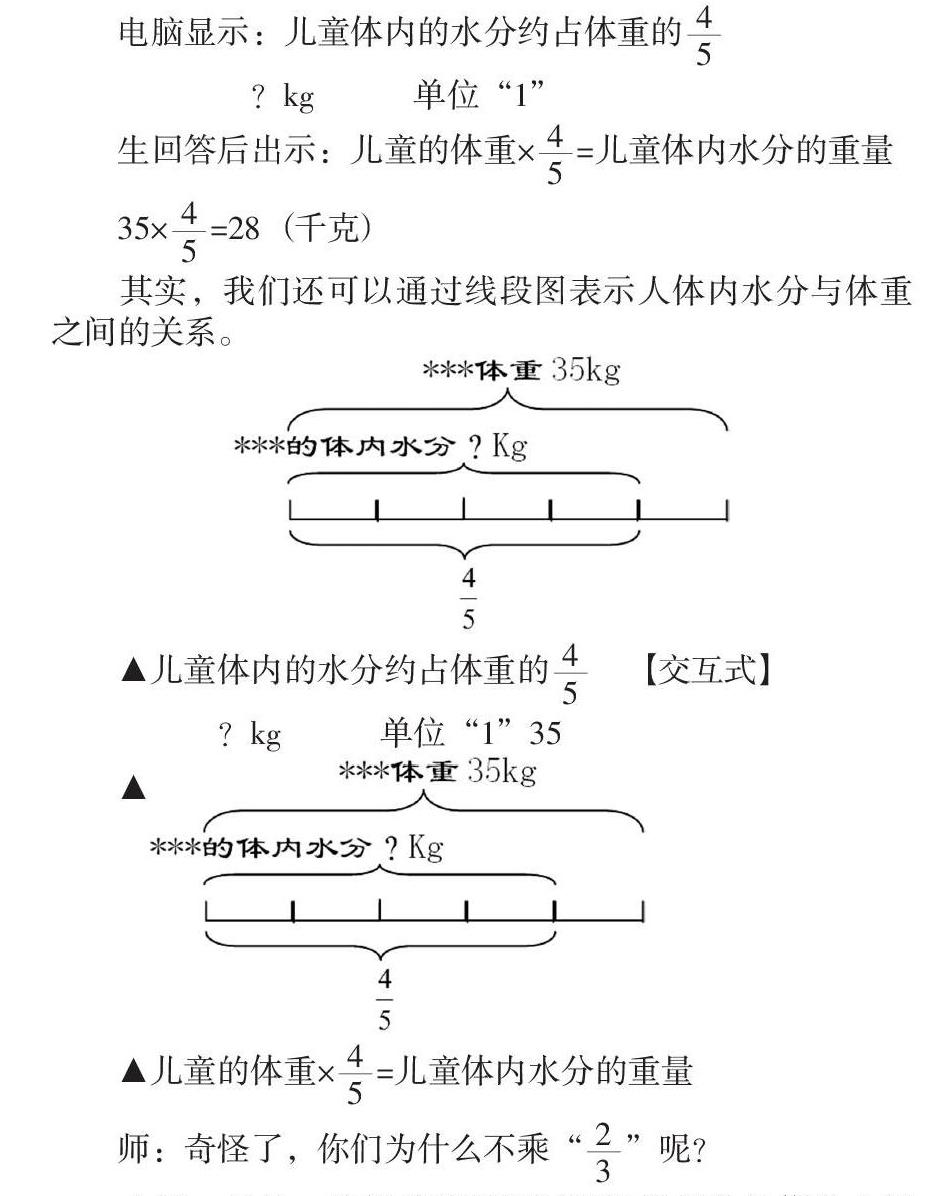
其实,我们还可以通过线段图表示人体内水分与体重之间的关系。
■
▲儿童体内的水分约占体重的■ 【交互式】
?kg 单位“1”35
■■
▲儿童的体重×■=儿童体内水分的重量
师:奇怪了,你们为什么不乘“■”呢?
小结:是的,我们必须根据问题选择相关的信息去解决问题,特别在解决分数应用题的时候,一定要找准“单位1”。而我们在解决有关分数问题的时候,一般有三种方法:第一,借助有分率的句子找出单位“1”和所求数量,然后得出此题的数量关系;第二,可以借助线段图清楚表达单位“1”和所求数量之间的关系;有了这两种方法为基础,我们搭建解题的数量关系式就轻而易举了。
4.揭示课题(略)
二、引导探究,解决问题
1.课件出示例题
根据测定,成人体内的水分约占体重的■,儿童体内的水分约占体重的■。小明体内有28kg水分。小明重多少千克?
2.合作探究
(1)独立思考,理清关系。
师:请选择一种喜欢的分析数量关系的方法,先分析好数量关系,会画线段图的,也可以画上线段图帮助自己理解,再列式计算。
■
3.学生汇报(展示学生作品,板书)
师:因为除法是乘法的逆运算,所以,根据乘除法之间的关系,我们除了可以用方程解决以外,还可以直接用除法来计算。
4.回顾与反思
(1)如何检验结果是否合理?
(2)题目里面还有“成人体内的水分约占体重的■”这一信息,有用上吗?为什么?
小结:有时候题目中出现的信息比较多,但并不是所有信息都是解决问题所需要的,我们要善于通过思考和分析,根据问题筛选出有用的信息来解决问题。
(3)方法对比。(同时出示两个线段图)
①和前面复习题进行比较一下,看看这题和复习题有什么相同的地方?
②这题和复习题有什么不相同的地方?
强调:解决分数乘除法,关键是分析分率句。【PPT强调】
三、看书质疑(P37)
四、联系实际,巩固提高(略)
……
一节课下来以后,从复习、新知再到对比反思,用时已经超过25分钟,比较的费时。而且,在教学的过程中,教师强调了分析数量关系,列了乘法的数量关系式,但又允许学生既可以用列方程的方法,也可以用除法去解决问题。学生例题似乎很懂,但在练习环节,感觉学生就无所适从。学生在做练习的时候,不知该用乘法还是用除法:有人写了乘法关系式,可是又很想用除法算,因为除法书写简便,能俘虏孩子们的心,最终把乘法数量关系式擦走,硬写了个毫无意义的除法关系式,甚至有些孩子直接列了乘法算式……感觉就是孩子原来心里好像挺清楚明白的东西,最终,变得很混乱很模糊,所以这节课的教学效果……费时而凌乱,极其低效。
究竟怎样修改才会更合理呢?该怎么处理好乘和除的关系,不会让学生有纠结的感觉呢?“具体量÷对应的分率=单位‘1”这一公式,这节课是否需要告诉学生呢?根据学生的心理认知特点,要让学生要知其然也要知其所以然,有了充分认识才能内化为自己所掌握的技能。
因此,我对教学设计重新进行定位,“善用旧知”,以旧有的分析数量关系方法分析数量关系;“迁移新知”,在原有分数乘法的知识基础上写出数量关系式;“沟通关系”,在得出数量关系式的基础上,用列方程解决“单位1”不知道的问题,并以列方程教学为主;“内化技能”,在列方程已经掌握相对熟练和有充分感知的情况下,再根据乘除法之间的关系,渗透“已知一个数的几分之几是多少,求这个数可以用除法来计算”。
经过反复的思考和修改,最终确定第二份教学设计。
【教学设计2】
一、复习旧知,回顾方法
1.激趣引入
由“水润”一词引入人体内的水分占体重的几分之几的话题
PPT出示:
①根据测定,成人体内的水分约占体重的■;
②儿童体内的水分约占体重的■。
2.复习分数乘法应用问题的分析方法与数量关系
(1)解决“多余信息”。(例4的其中一个知识点前移)
師:如果知道小明的体重是35千克,你们能帮他算出他体内水分的质量吗?
是不是这两个信息都用上呢?为什么?
小结:是的,我们在解决问题的时候,要根据问题选择相关有用的信息。
整理信息与问题,板书:
小明的体重是35千克,儿童体内的水分约占体重的■。小明体内的水分重多少千克?
(2)复习分析数量关系的方法。
学生分析关键句,画线段图,写数量关系式并列式解答。
强调:根据分数乘法的意义写出数量关系式和列式。
板书:分数乘法的意义:求一个数的几分之几是多少,用乘法计算。
二、学习新知,迁移方法
1.调整复习题的条件与问题,引出例4,揭示课题。
2.解决问题
(1)复习解决问题的步骤。
(2)阅读与理解
你知道了什么?与刚才的复习题比较,什么变了?什么没变?
(3)分析与解答
关键句没有改变,意味着什么?(解题的思路与分析数量关系的方法应该也不变,线段图等不需要重新画)条件和问题改变了,那在原来的基础上怎么改一改就行呢?请大家想一想,说一说。
(学生到黑板上修改)
关键句:儿童体内的水分约占体重的■
? 35
(28) (?)
关系式:小明的体重×■=小明体内水分的质量
35 ?
? 28
师:体重不知道,怎么办?可以怎样解决呢?
学生尝试列式计算。
汇报提问:为什么列方程?用除法计算,你根据的是什么?(要紧扣数量关系式)
(4)回顾与反思
师:回顾与反思环节需要我们做些什么?
PPT出示:检查审题与解题方法是否正确。
检验计算结果是否合理、正确。
回顾解题过程,总结解题的思路与方法。
▲学生检验计算结果
▲回顾解题过程,通过对比总结解题的思路与方法。
①这一道题是怎样从复习题变过来的呢?它整一个解题的思路与步骤跟复习题相比较,有什么相同的地方?
小结:解决问题仍然是用我们已经熟悉的方法来分析数量关系,仍然是根据分数乘法的意义列出乘法的数量关系式进行解答。
②为什么复习题列乘法算式,而这一题却列方程或除法呢?
3.看书质疑
三、巩固练习,运用方法
师:既然列方程的方法是顺着来思考的,那么我们先巩固列方程的方法,好吗?
1.练习八第1题
我国幅员辽阔,东西相距5200km,东西距离是南北的■。南北相距多少千米?
强调:根据乘法的意义列出等量关系式。若有学生用除法列式,要强调依据的也是乘法的等量关系式。
2.练习八第4题:求图书馆共有多少本书?
强调:应根据问题选择相关有用的信息去解决问题。
3.按要求选择合适的条件与问题。
乘法计算:
女生人数占全校总人数的■
列方程:①女生 240人,②全校有640人,
③女生有多少人? ④全校有多少人?
全校人数×■=女生人数
640 ?
? 240(下转第6版)
(上接第5版)
【设计意图:强调学生要紧扣关键句,得出数量关系式。当全校人数知道,求女生人数时,用乘法计算;当女生人数已知,求全校人数的时候,就列方程来解决了。】
4.选一选。
( ) ( )
①420×■ ②解:设总长为x米。 ①180÷■
■x=180
【设计意图:既复习了依据“总长×■=已修的长度”这个数量关系式得出列方程解决的方法;同时结合线段图比较直观地引出:具体量÷对应的分率=单位“1”的量这种较简单的解决问题方法】
5.填空:( )的■是60。
你是怎样算的?为什么用除法来计算呢?(结合关系式“( )×■=60”)
也就是说,已知“一个数”的几分之几是多少,求原来这个数,可以直接用除法来计算。
6.PPT出示
今天我们学习的例题与做的这几道练习,都是已知一个数的几分之几是多少,求这个数,都可以用列乘法方程或列除法算式的方法来解决,依据都是分数乘法的意义。
四、总结反思,强调方法
“善用旧知、迁移新知、沟通关系、内化技能。”学生在分数乘法这一旧知的基础上,通过数量关系,先理解并掌握了用方程解决“已知一个数的几分之几是多少,求这个数”这一问题的方法,再通过一系列的对应及变式练习,能让学生在充分的认识和理解以后,感受到,除法是乘法的逆运算,在解决“已知一个数的几分之几是多少,求这个数”这一类型的问题时,还可以用“具体量÷对应的分率=单位‘1”这一较简单方法来解决。数学教学强调教会学生善于选取优化方法去解决问题,相信学生们也更乐于选择此方法去解决问题。在“知其然也知其所以然”的基础上掌握了一种更优化的方法,何乐而不为呢?
