基于滚石运动参数的防护网数值模拟
2020-08-06刘成清陈玉满
刘成清, 陈玉满
(西南交通大学土木工程学院,成都 610031)
滚石在自重以及外力作用下脱离母体或原位,以自由落体、抛射、弹跳、滚动、滑动或以多种运动方式的组合形式顺坡向下运动,冲击公路、铁路等沿线,威胁行车及人身安全。被动柔性防护网因其“以柔克刚”的结构性优势功能,被广泛运用于工程实践的有效防护措施之一。何思明等[1]给出了滚石碰撞具体的计算公式;章广成等[2]研究了碰撞恢复系数的特征及影响因素;冯晓等[3]基于概率统计理论对滚石运动轨迹进行模拟;陈颖骐等[4]基于Hertzj接触力学和Thornton弹塑性假设建立了滚石对构造物的冲击力修正方程;叶四桥等[5]研究表明滚石质量、坡面状态、坡度、下落高度对切向恢复系数影响较大;许婧璟等[6]基于能量跟踪法研究岩石破碎对运动轨迹影响;Hambleton等[7]考虑“子弹效应”提出被动柔性防护网临界动能的数值模型;Tran等[8]进行了试验与数值仿真结果表明数值仿真可以代替试验进行防护网设计选型;刘成清等[9-12]、Liu等[13]和Yang[14]研究了被动柔性防护网的整体变形以及减压环、钢柱等关键构件的耗能及其破坏机理。目前对柔性防护体系中网片、消能件及钢丝绳网等组件研究较多。对滚石滚动的某个阶段如碰撞基于理论与试验也有报道,但对滚石整个运动阶段的理论与试验研究相对较少,基于确定的滚石运动参数被动柔性防护系统研究目前也很少。基于接触理论和动力学理论对滚石从初始运动阶段到最终停止进行了理论推导,对影响滚石运动状态的坡度与坡面材料展开研究,利用成熟的滚石模拟软件获取可以用于设计的运动参数。利用ANSYS/LS-DYNA对落石撞击网片进行数值仿真验证选型合理性。
1 滚石运动状态
典型的滚石运动状态一共经历五种运动情况分别为自由落体运动、抛射、碰撞、 滚动滑动,如图1所示。
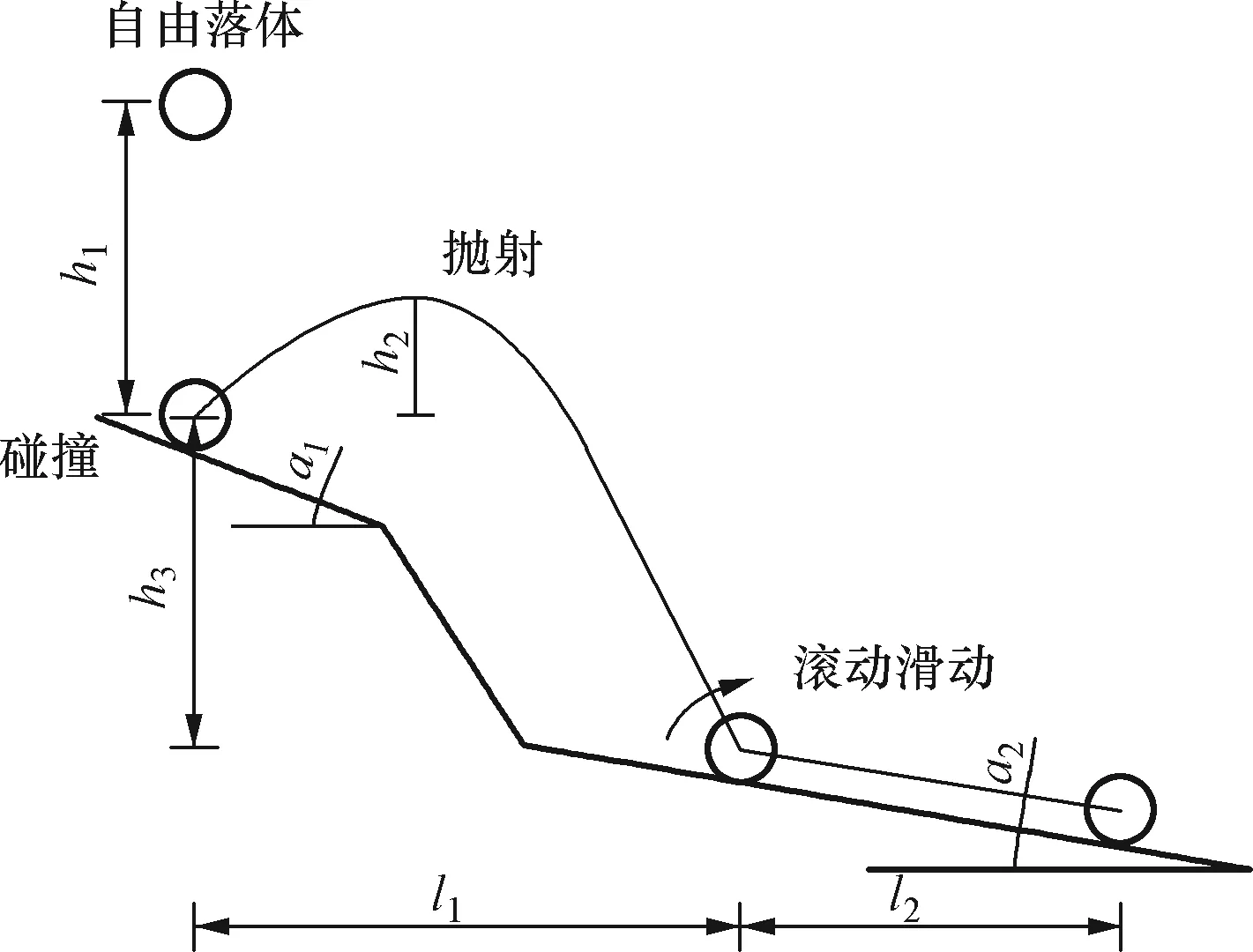
h1为滚石自由落体的高度;h2为滚石斜抛上升的高度;h3为斜坡上碰撞下降的高度;α1为第一段斜坡的坡度;α2为第三段斜坡的坡度;α1为第一段斜坡的坡度;l1为滚石发生碰撞到滚动滑动阶段水平位移;l2为滚石滚动滑动到停止运动阶段水平位移图1 滚石运动示意图Fig.1 Rolling stone motion diagram
1.1 自由落体阶段
滚石的自由落体运动,是在重力作用下脱离母岩, 也或者在只有一定的初始角速度开始运动,大部分是启动阶段中的坠落或者倾倒导致。由于空气阻力一般只有重力1/20左右,故一般忽略不计,角速度在坠落过程中则认为保持不变,滚石运动轨迹公式为
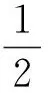
(1)
(2)
式中:h1为自由落体的高度;g为重力加速度,g=9.8 m2/s;v为滚石的下落速度。
1.2 碰撞阶段
以 Hertz 接触力学为计算基础,假定滚石为刚性体,碰撞时地面只发生法向变形,切向未发生变形。将碰撞过程分为两个阶段:压缩阶段和回弹阶段。压缩阶段指落石从与地面接触到压缩地面产生最大的弹塑性变形过程,分为弹性加载阶段与塑性加载阶段;回弹阶段指从最大弹塑性变形位置弹性恢复至残余塑性变形位置的过程即回弹卸荷阶段。碰撞过程假定滚石与坡面的碰撞发生在一个碰撞点上,不产生滑移。Azzoni等[15]研究结果也表明碰撞过程滑移确实极少发生。
1.2.1 弹性加载阶段
接触力学[16]中Hertz应力分布函数:
(3)
法向位移函数:
(4)
位移边界条件:
μz1+μz2=δ-(1/2R)r2
(5)
将式(4)代入式(5)中,得:
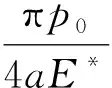
(6)
由牛顿第三定律:
(7)
式中:
a=πp0R/2E*
(8)
(9)
(10)
滚石对地面的荷载为
(11)
联立式(7)~式(11)得:
(12)
式中:μz1、μz2分别为碰撞前后法向位移;E*为滚石与地面接触的等效弹性模量;p0为最大接触应力;a为接触区半径;r为距离接触区中心的距离;R为滚石与坡面的等效半径;δ为贯入量;E1、E2分别为滚石和坡面的弹性模量;ν1、ν2分别为滚石和坡面的泊松比;R1、R2分别为滚石和坡面的等效半径。
Jackson 等[17]研究的弹塑性材料应力与滚石砸入深度间的关系:
(13)
C=1.295e0.736v
(14)
Cσy=min[C(v1)σy1,C(v2)σy2]
(15)
联立式(13)~式(15)可得:
(16)
由能量守恒定律:
(17)
联立式(16)和式(17)得:
(18)
式(18)中:σy1、σy2为碰撞前后的屈服应力;V为土体第一次屈服时的瞬时速度;C为临界屈服应力系数;V2为滚石碰撞后的速度;δy为土体初始屈服时的贯入量;σy为土体的初始屈服应力。
1.2.2 塑性加载阶段
(19)
V3=0,此时滚石达到最大砸入深度,有:
(20)
基于土体的线弹性本构得:
Pep=σy
(21)
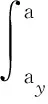
(22)
联立式(20)~式(22)得:
Fy(δm-δy)
(23)
式中:Pep为塑性加载阶段的接触应力;V为瞬时速度;Vy为弹性阶段过渡到塑性阶段的临界速度;W*为塑性加载阶段的应变能。
1.2.3 回弹卸荷阶段
回弹卸荷阶段土体的应力应变关系与弹性阶段保持一致。
(24)
(25)
式中:Prep为回弹卸荷阶段的荷载;V2、V1分别为碰撞后和碰撞前的速度;δ为塑形残余变形;δm为最终变形量。
法向的恢复系数为
(26)
根据胡厚田等[18]的研究, 考虑瞬间摩擦的作用, 切向速度大小在碰撞过程中损失率约为10%,切向恢复系数et可考虑的坡面材料进行适当取值,et为0.8~1。
1.3 抛射阶段
由于空气阻力只占到滚石重力的1/20左右,通常忽略不计,假设滚石刚经过碰撞后获得速度V2,经过抛射运动后的速度为V3,h3为滚石斜抛初始点与落点的高度差,h2为滚石初始点与最高点的高度差,θ为抛射角度。根据能量守恒定律:
(27)
(28)
水平位移:
(29)
1.4 滚动滑动阶段
滚动、滑动阶段即滚石在自重作用下考虑斜坡的滚动/滑动摩擦沿着坡面向下运动,滚动、滑动阶段运动状态相似,一般是滚石运动停止的最后一个运动阶段,可由运动学知识获得滚石滚动阶段的加速度:
a=(gsinα-gkcosα)
(30)
滚动阶段的瞬时速度变化:
(31)
滚动阶段的能量变化:
(32)
k=tanΦd
(33)
(34)
式中:V4为滚石滚动前的速度;α为斜坡坡角;a为滚动、滑动阶段加速度;k为滚动摩擦系数/滑动摩擦系数;Φd为摩擦角;s为滚动距离;sm为停止滚动距离。
2 滚石运动状态的影响因素
2.1 碰撞与抛射滚动能量耗散比较
1.2~1.4节给出了碰撞、斜抛及滚动滑动阶段的速度能量计算公式,由于δreu需要试验测得,采用已经成熟的滚石运动轨迹模拟软件Rocfall软件进行模拟。简化模型,选取一端坡度为45°的斜坡进行模拟,通过设置初始速度使初始动能保持一致,比较三者的能量损耗差异。滚石的初始质量为10 kg。坡面材料为基岩露头的恢复系数取值采用Rocfall软件默认取值,法向恢复系数为0.35,切向恢复系数为0.85,摩擦角为21.8°[16]。如表1所示基岩滚动摩擦系数为0.40,利用式(32)求得。滚石运动轨迹如图2所示,能量变化如图3所示。

表1 滚动摩擦系数[16]Table 1 Coefficient of rolling friction[16]

图2 滚石运动轨迹Fig.2 Rolling stone movement track

图3 滚石动能变化Fig.3 Rolling stone kinetic energy change
运动轨迹与能量变化显示斜抛碰撞阶段先做抛物线型然后陡降,滚动阶段能量图显示直线均能一定程度上验证第1节推导公式的合理性。滚石第一次撞击损耗的能量336.9 J,第二次撞击损耗的能量315 J,到达x=20 m时,滚石做斜抛碰撞运动的动能为 1 415.6 J,做滚动时为1 400 J,说明滚动阶段所造成的能量损耗要比斜抛碰撞阶段要大。
2.2 坡度对碰撞,抛射,滚动的影响
l为水平总坡段的长度,l=180 m;h为坡段总高度,h=180 m;d为水平分段长度,d=60 m,滚石的初始运动参数为水平速度为10 m/s,竖直速度为10 m/s方向向上,滚石初始质量设为10 kg。边坡材料均为基岩裸露材料参数2.1节已说明。滚石在不同坡度的运动轨迹如图4所示,能量变化如图5所示。
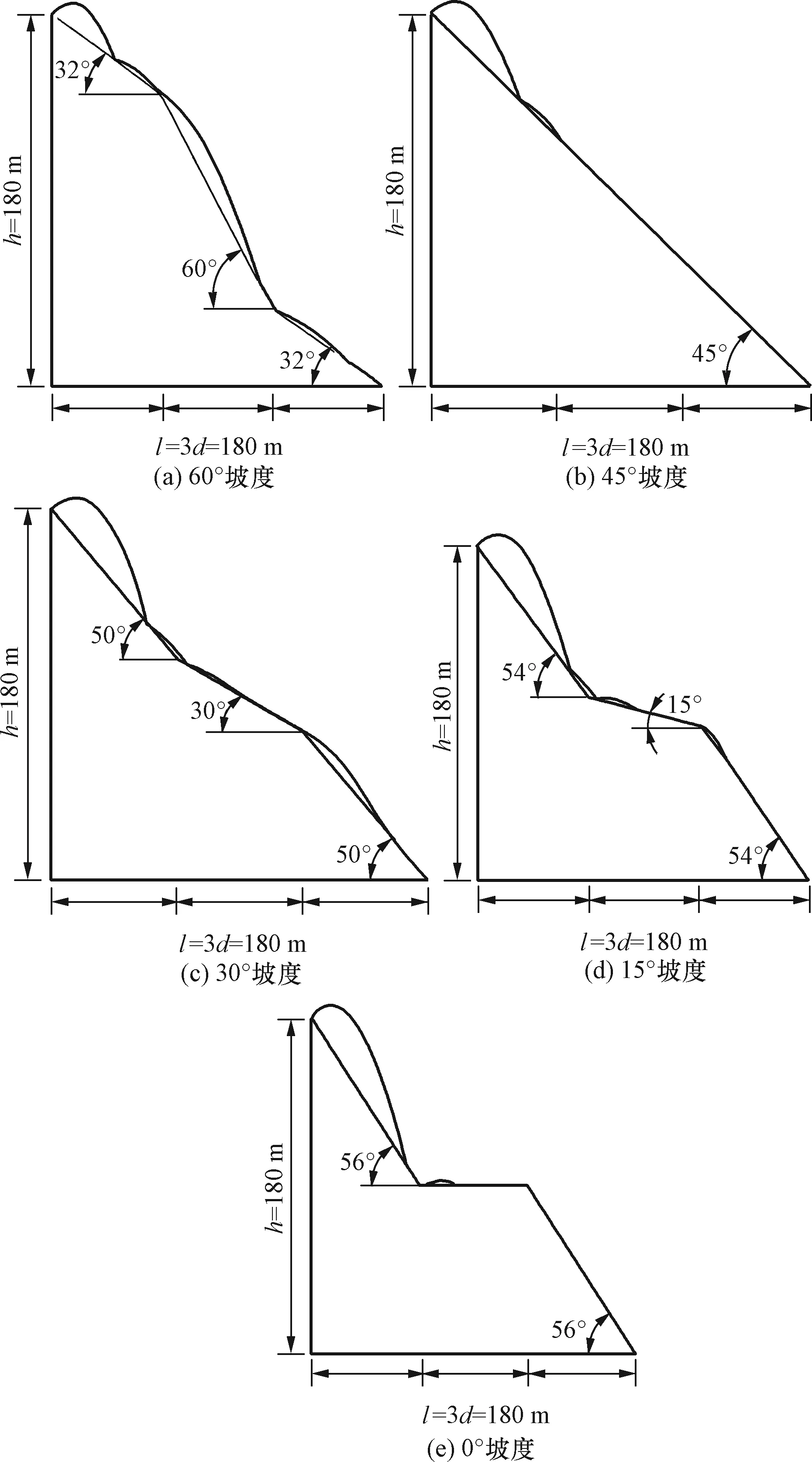
图4 不同坡度滚石运动轨迹Fig.4 Rolling stone movement track at different slopes

图5 不同坡度滚石动能量变化Fig.5 Dynamic energy change of rolling stones with different slopes
如表2所示,不同坡度中,以中间坡段45°坡度作为参照,中间坡度为30°,60°时,造成的动能损耗基本一致损耗差别仅为26.7 J,两者滚石的运动轨迹也大致相同,而全部坡段坡度均为45°的坡段所造成的能量损耗最少,与中间坡段坡度为60°相比,动能损耗差别为2 897.3 J,设置了平台的斜抛滚石能够有效较少碰撞次数提前终止运动。中间坡度为60°、30°的斜抛可以概括为两缓一陡坡段和两陡一缓。能加大滚石能量的损耗。

表2 滚石碰撞次数及能量Table 2 Number of rolling stone collisions and energy
2.3 坡面材料对碰撞,抛射,滚动的影响
表3的恢复系数取值采用Rocfall软件默认取值,摩擦角取自文献[16]。

表3 边坡材料参数Table 3 Material parameters of slope
如图6所示,清洁基岩面和土壤与植被覆盖的边坡能减少碰撞抛射的次数,采用土壤和植被材料所覆盖的坡面能损耗滚石的能量最大,相比其他坡面材料使滚石提前停止运动,清洁基岩覆盖的坡面所造成滚石能量的损耗相比其他坡面要少得多,相比基岩露头、土壤植被覆盖的坡面,其他坡面材料覆盖的坡面最终对滚石的能量损耗大致相同,且三者的运动状态也基本一致。基于土壤和植被材料所覆盖的坡面对滚石能量影响最大,可考虑在坡面表面铺设土壤与植被增加滚石动能的损耗。
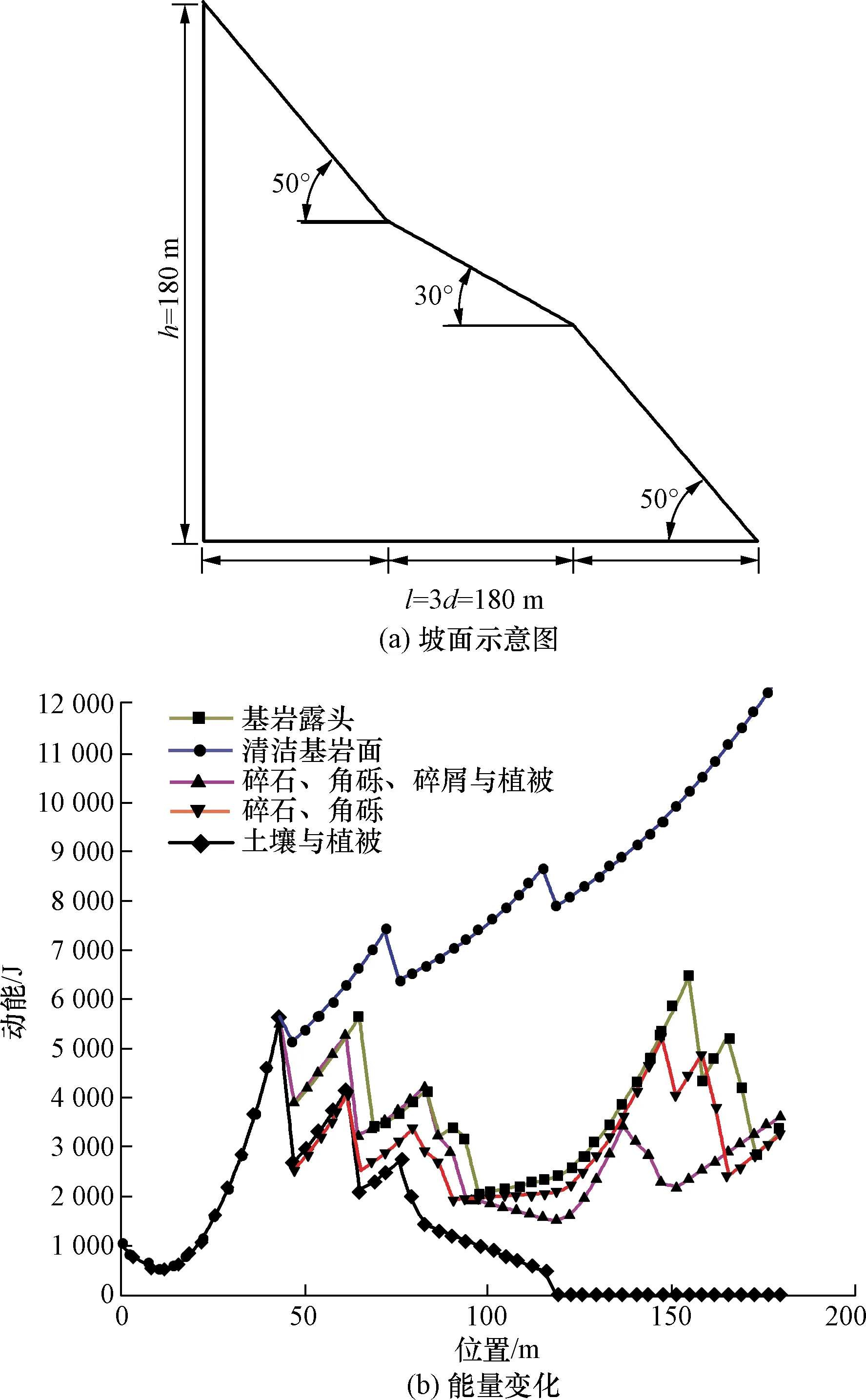
图6 坡面示意与能量变化Fig.6 Slope indication and energy change
3 滚石运动参数
3.1 案例与模型
边坡位于滇池盆地西北部边缘,属于崩塌堆积地貌。选取危岩体高程位于 2 125~2 155 m,与高速公路路面高差最大达260 m,属于特高位危岩体。呈不规则块状,该危岩体下部存在凹腔,属于悬挑式崩塌危岩体。在地震作用下发生崩塌剥落,对行车安全与人身安全危害极大。考虑不安全因素假设因地震作用造成质量为50 kg的滚石坠落,初始速度设为0,选取模拟滚石次数为 1 000。起始运动为滚动。
3.2 运动轨迹
图7为滚石的运动轨迹及一般防护装置布置位置。
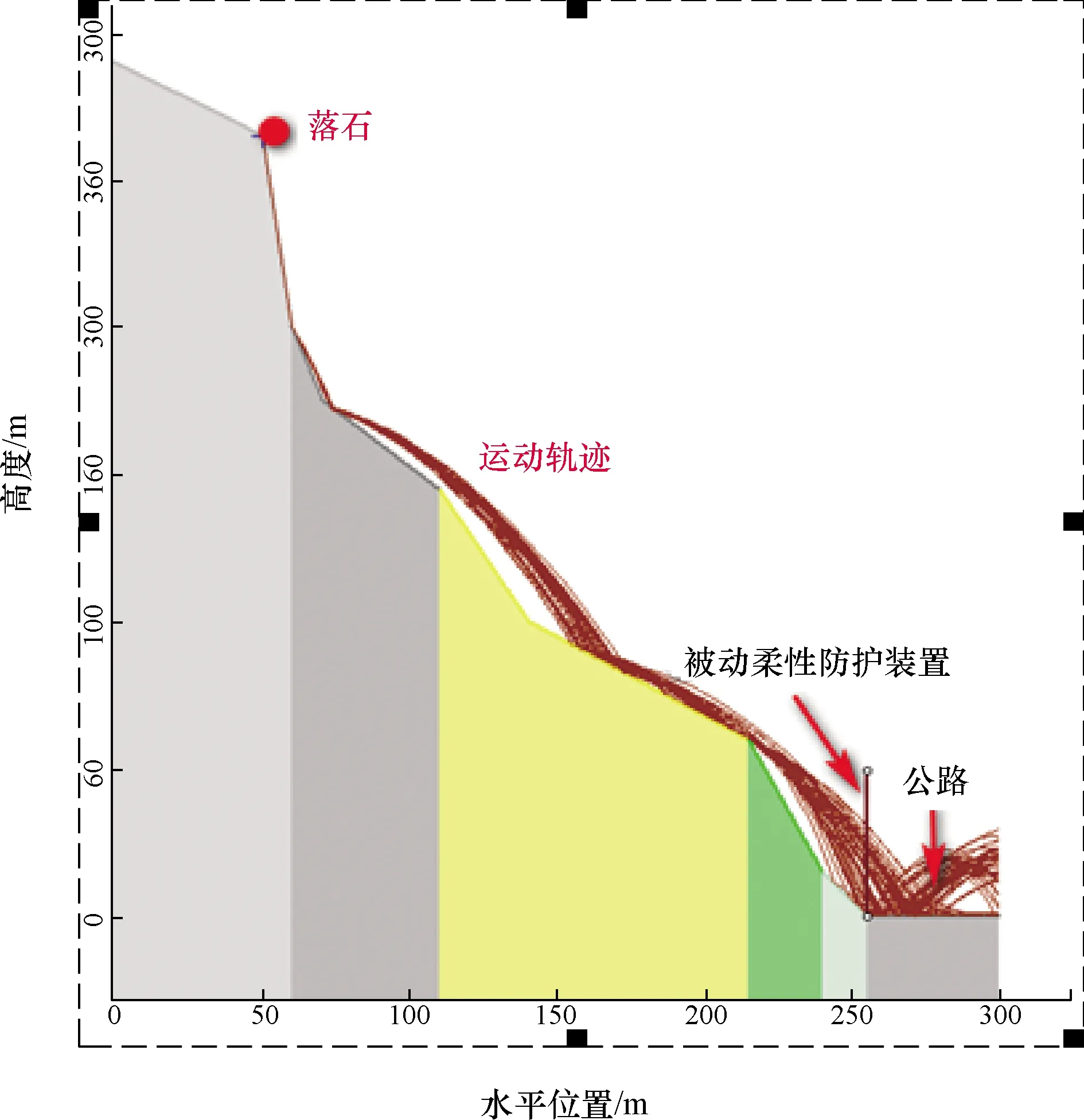
图7 滚石运动轨迹Fig.7 Rolling stone track
3.3 滚石弹跳高度、能量、速度参数
从图8可以看出,滚石的起始做滚动运动,在经过碰撞斜抛运动离开斜坡,在水平位置69.7 m左右达到弹跳的最大高度,此时距离斜坡5.5 m,接着做向下的斜抛运动水平位置242.4 m时离斜坡的高度达到15.5 m,最后在水平位置260.6 m时落到公路上弹跳高度达到17.1 m。滚石的总动能变化,在水平位置为75.8、130.3、254.5 m时,滚石的总量分别达到34.2、50.4、38.5 kJ。一般的防护装置均设在公路边缘附近,但在这些位置拦截时拦截难度较大。

图8 滚石弹跳高度及能量分布Fig.8 Rolling stone bounce height and energy distribution
不利于防护装置发挥最大耗能,且弹跳高度较高已超过防护装置的防护范围,而水平位置130.3~215.2 m时,滚石总能量呈现减小的趋势,在水平位置151.503 m的滚石能量与速度较低,可有效降低防护网因为子弹效应造成的穿透,故此处设置被动防护网装置较为合适,滚石在此位置的动力参数分布如图9所示。
如图9所示,滚石的速度主要集中在14.75~32.99 m/s,29.95 m/s时滚石数目为303,占比30.3%,滚石的弹跳高度分布在0~2.72 m,1.60~1.74 m滚石数目分布为173。被动柔性防护装置网片易因子弹效应[7]被击穿,取滚石速度32.99 m/s,滚石最大弹跳高度为2.72 m。
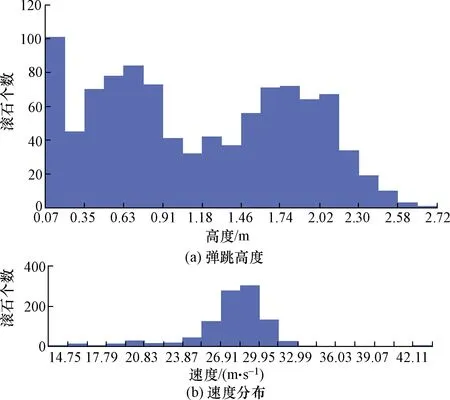
图9 x=151.503 m弹跳高度与速度分布Fig.9 x=151.503 m bounce height and velocity distribution
4 滚石灾害治理
被动柔性防护网因其“以柔克刚”的结构性优势功能,是治理滚石灾害的有效防护措施之一。基于被动柔性防护网装置大部分是网片破坏,简化模型建立网片以及支撑绳系统。基于获取的滚石运动参数及弹跳高度分布,滚石质量为50 kg,考虑安全储备运动速度取34 m/s,基于滚石弹跳高度最大2.72 m选用3.3 m×6.6 m环形网,网型选用R7(7圈环绕)/3 mm/300 mm较为合适,等效截面半径26.42 mm2,支撑绳半径8 mm,等效截面面积200.96 mm2,利用ANSYS LS-NYNA进行数值仿真分析,材料参数如表4所示。
表4 材料参数Table 4 Material parameter
从图10可以看出,滚石砸在防护网的中心位置,在网片中心位置最大竖向位移为2.30 m,且未发生破坏,在滚石质量较小的情况下,能阻止较高速度的滚石冲击,避免对过往车辆造成严重危害,说明基于滚石运动参数的防护网选型合理能有效防治滚石灾害。
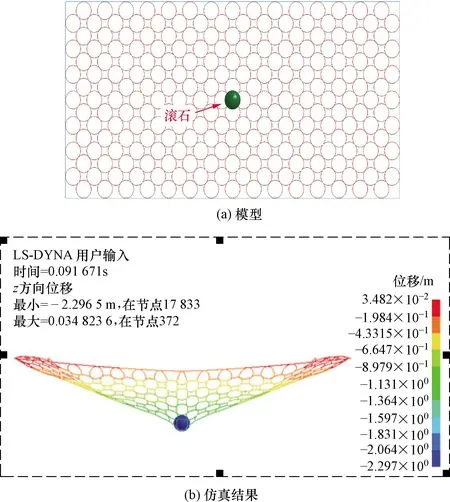
图10 滚石防护网模型及仿真Fig.10 Rolling stone protective net model and simulation
5 结论
基于Hertz接触力学、运动学公式,对滚石运动各阶段运动公式进行了推导分析,研究了坡度、坡面材料对滚石运动状态及能量损耗的影响,通过工程案例分析获取了滚石灾害防治所需的运动参数与弹跳高度,利用数值仿真软件对选取的防护网系统进行了验证。得到以下结论。
(1)滚石斜抛射运动阶段能量变化呈现抛物线型,碰撞阶段法向恢复系数与碰撞前的速度成反比,滚动滑动阶段滚石动能与速度位移均成线性正比关系。
(2)碰撞斜抛与滚动相比较,滚动阶段造成的能量损耗更大,坡度与斜坡材料对滚石的运动状态具有很大的影响,与45°斜坡相比较,两缓一陡,两陡一缓斜坡对滚石的能量损耗更大,清洁基岩材料覆盖的斜坡对滚石的能量损耗影响最低,通过铺设土壤和植被能有效降低滚石的能量,减轻滚石灾害破坏。
(3)通过Rocfall软件可获取滚石运动参数,速度、能量、弹跳高度用于防护装置的位置布置及选型设计如被动防护网装置。
(4)利用ANSYS/LS-DYNA可进行被动防护装置选型设计降低防护成本,验证选型合理性,通过不断调整被动防护网构件参数来进行优化设计,通过适当选取R7(7圈环绕)/3 mm/300 mm,并通过仿真分析结果表明设计选取的网片合理对滚石能有效拦截。
