基于改进Markov预测算法的电磁态势预测技术
2020-08-06史雨璇陈永游张东甲鲁加战仵志鹏
史雨璇,陈永游,张东甲,包 军,鲁加战,胡 进,仵志鹏
(1.中国航天科工集团8511研究所,江苏南京210007;2.中国航天科工集团有限公司,北京100037)
0 引言
随着电子设备的广泛部署,急需大量的专业技术人员对专业设备进行操作,需要通过专门的训练系统对相关人员进行训练[1]。但很多训练单位依然采用传统的方式完成训练学习,这种方式投入大、消耗多、可重复利用率低[2]。如果通过训练系统,再结合实际的场景采集数据进行实际数据的训练,可提升训练真实性。但由于实采数据的分析处理结果速度慢,准确率低,容易造成训练过程中的数据时延问题,影响训练效率[3]。为提升预测结果准确性,本文提出改进的Markov预测算法,对电磁态势预测训练提供更精确的辅助,在训练系统中起到重要作用。
1 电磁态势预测训练系统
为解决实际数据采集过程中的时延问题,有研究者在训练分析的并行条件下,构建训练辅助模块,利用Markov预测手段,实现对于真实数据的预测处理,帮助参训人员和指挥员对训练结果进行实时控制[4]。但是,Markov预测算法自身的收敛程度有限,导致预测结果和真实结果之间存在一定差异,因此有必要改进Markov算法。电磁态势预测模拟仿真训练的系统组成如图1所示。根据图1,基于具体的实采数据进行态势分析预测的流程为:第一步对采集到的真实态势数据进行提取,得到目标的电磁态势信息,其中包含:时间信息、位置信息、辐射源参数信息、目标辐射源工作模式信息、行为规律信息以及功率值信息等。第二步将提取到的数据信息进行数据清洗、数据融合等预处理,如图1虚线箭头指向部分。第三步主要为参训人员将预处理得到的数据信息进行预测训练,在完成训练后和真实采集的数据进行比对,由于真实数据采集的时延特性,这种手段无法做到实时验证。因此,在本文的改进方法中,第三步把经过预处理得到的全部数据信息发送至训练系统进行人员分析训练,同时将经过预处理的时间、位置、辐射源参数信息进行算法级的态势预测处理。第四步将以上2部分的共性处理结果进行比对,将算法级态势预测的位置信息、航迹信息和功率值结果作为标准,对参训人员的处理进行核对,完成电磁态势预测训练的考核评估任务。
由图1可看出,虚框部分是本系统的核心,必须通过快速准确的算法获得预测结果,才可支撑对训练者的训练结果进行评价,预测结果的准确与否直接影响了训练者的考核结果。现阶段的训练辅助模块中主要使用了Markov预测算法进行预测。
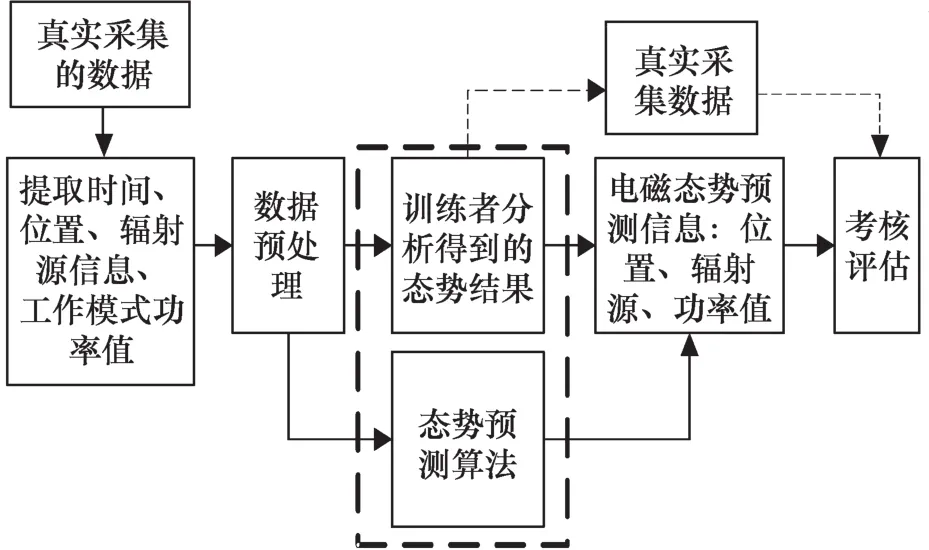
图1 电磁态势预测模拟仿真训练系统组成
2 Markov预测算法
Markov过程是一种特殊的随机运动过程[5]。即如果随机过程X(n)在时刻(t+1)的状态与t时刻的状态之前的状态无关,只与X(n)在t时刻状态的概率分布有关,即满足下式,则X(n)为Markov随机过程。

在利用Markov预测模型进行预测时,如果被预测的对象有m种状态,即状态空间为E={0,1,2,…,m},如果用fij表示样本数据中从状态i转向状态j的次数(i,j∈E,这里仅讨论一步转换成功的情况),由fij组成的矩阵(fij)i,j∈E为转移频数矩阵。由状态i向状态j的概率Pij称为转移概率。

Markov预测模型是利用初始状态分布和状态转移矩阵去预测未来的数据,现假设有一随机变量X(n),其状态空间为E={0,1,2,…,m},当前时刻的状态分布为p(n),初始状态分布为p(0),状态转移概率矩阵为P,则会有下式成立:

根据以上的分析过程可知,在利用初始状态信息做预测的时候,随着预测次数的增加,预测值与真实值之间的误差越来越大。
3 改进的Markov预测算法
传统的Markov预测模型有2个明显的不足,会给预测结果带来较大的误差,一是对于状态的划分通常依靠经验去划分(硬划分),划分结果因人而异;二是预测值的估算通常是采用最大概率原则进行计算的,即只考虑最大概率的状态信息。这2点将对预测精度产生较大的影响。
在传统的Markov预测模型分析结果的基础上,为提高预测结果的精度,同时也为了让Markov预测模型能较好地应用在电磁分布趋势的预测上,本文将模糊C均值算法和传统的Markov预测模型相结合,利用基于模糊C聚类算法对原始序列进行模糊序列的划分,然后计算原始序列中每个值关于模糊状态中各状态的隶属度向量和转移概率,并将待预测点处的隶属度向量作为计算预测值的权重,完成预测计算。
1)模糊C均值算法
模糊C均值(FCM)算法是一种基于目标函数的模糊聚类算法,其基本思想是将相似度最大的对象划分到同一簇,而相似度最小的对象划分到不同簇[6]。
FCM算法的基本过程如下:
假设X={x1,x2,…,xn}是一个由n个数据构成的集合,利用FCM算法可以将集合X聚类为c(2<c<n)类。以V={v1,v2,…,vc}表示c个聚类中心,隶属度函数uij表示第j个样本数据对第i个聚类中心的隶属度,则FCM的目标函数及其约束条件为:
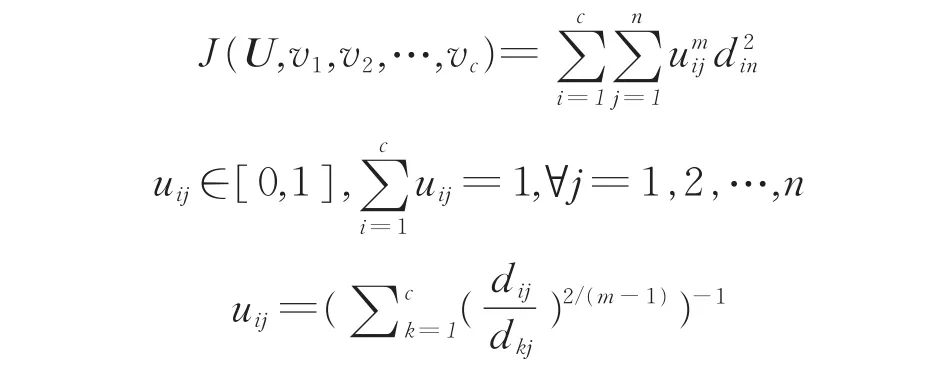
式中,U=(uij)c×n为隶属度矩阵为第j个样本数据到第i个聚类中心的欧氏距离,m是一个模糊 加 权 系 数 ,一 般m∈ [1,2,5],目 标 函 数J(U,v1,v2,…,vc)表示各个样本数据到聚类中心的加权距离平方和,J(U,v1,v2,…,vc)越小说明聚类效果越好。
2)改进Markov电磁态势预测
利用该模型进行预测的流程如图2所示。

图2 基于FCM的马尔科夫预测模型
现假设有一随机序列X={x1,x2,…,xn}(序列中的每个xi,i=1,2,…,n,都可以看成一个对象),在电磁态势预测中,将目标电磁态势中的位置信息、时间信息和辐射源相关参数信息或功率值作为输入可以得到预测的目标功率值及电磁态势相关航迹信息等结果,利用该模型进行预测的具体步骤如下:
1)首先利用FCM聚类算法对原始的序列X进行聚类,得到s个聚类中心v1,v2,…,vs,即s种状态;
2)计算隶属度矩阵U。即利用每个对象的xi关于状态空间中各个状态的隶属度uEi(xj)(i=1,2,…,s;j=1,2,…,n),得到各个对象的模糊向量

3)计算转移概率及转移概率矩阵,对于原始序列中的任意一个对象xi,令:
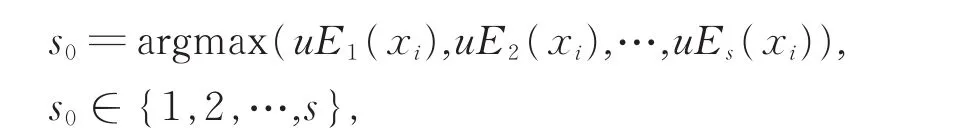
则xi=vs0,1≤s0≤s然后计算从状态i转向j的概率Pij=Nij/Ni,其中Nij是从状态i转向状态j的个数,Ni为状态i在原始数据序列中出现的次数,则状态转移矩阵为:
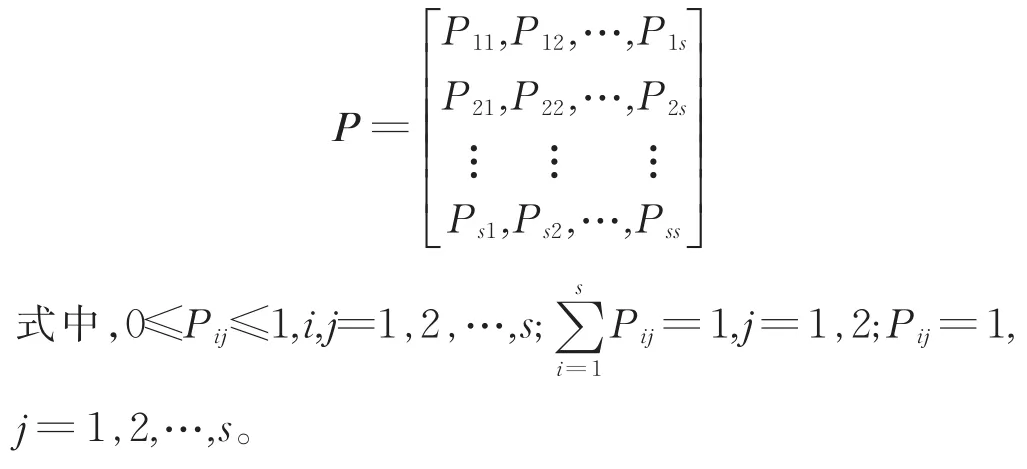
4)预测下一时刻的状态。对于各个状态的隶属度,如果:

则对象xn属于状态空间中的状态i0。可以根据前n个对象中,每个对象隶属于状态i0的隶属度计算出预测所需要的权重因子 {w1,w2,…,wn}。
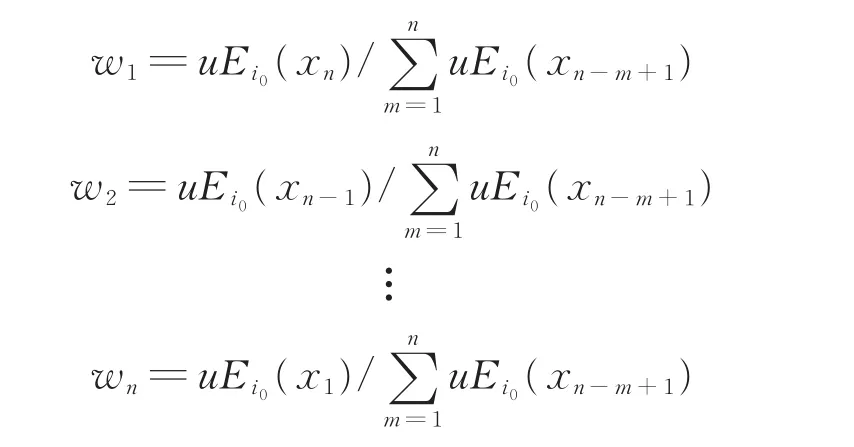
利用权重因子计算待预测点xn+1的隶属向量G(xn+1)满足:
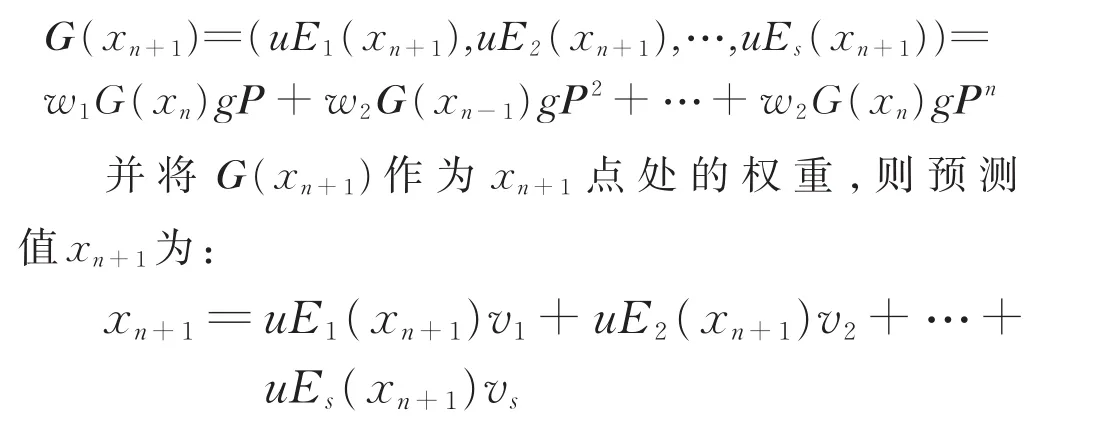
4 仿真结果展示
将FCM聚类算法和Markov预测模型相结合,利用FCM聚类算法对原始数据进行状态划分,避免了传统的Markov预测模型中的硬划分或依赖经验划分带来的误差,提升电磁态势预测的准确性。
将该方法运用在电磁态势预测训练辅助模块,比原有Markov预测模型直接运用在电磁态势预测训练辅助模块具有更接近于真实值的结果。
为验证真实效果,本文进行如下实验:
实验开始时首先选取处于不同位置的4个地点,采集了20个时刻的时间信息、位置信息和辐射源参数信息等电磁态势数据及功率值信息。在实验过程中,利用前15个时刻的数据作为先验信息数据,用于参与预测计算;后5个时刻的数据用于对本次预测的精度进行分析。其中的位置安排如下:位置一距离探测点设置为1 km;位置二距离探测点设置为3 km;位置三距离探测点设置为5 km;位置四距离探测点设置为7 km。
实验结果以功率值为参考依据进行比对,比对结果如图3和表1所示。
由以上结果可以看出,在相同距离内,相比于Markov预测算法,改进的Markov预测算法的预测准确率更高,预测效果更稳定,且在探测范围内,距离越远效果越明显。
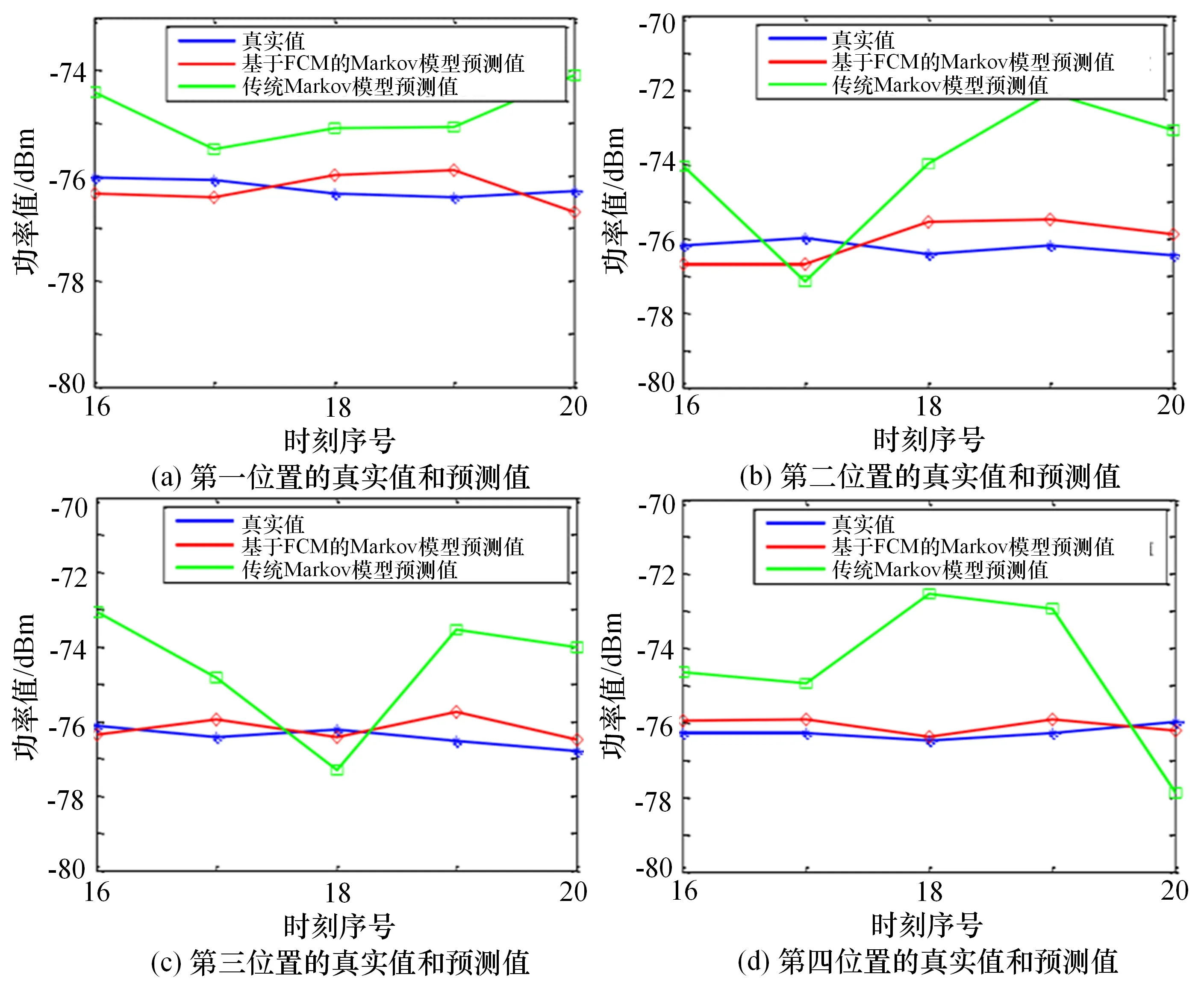
图3 数据中各个时刻的真实值和预测值

表1 不同位置数据预测值比对
5 结束语
相比于传统的Markov预测方法,基于FCM聚类算法和Markov预测模型结合的数据分析态势预测的结果在准确率和预测稳定性方面都有所提升。将改进的Markov预测算法运用在训练系统中作为训练辅助,可以更好地验证参训人员对于真实接收数据的训练效果。■
