基于逻辑回归模型的瓦斯浓度异常值检测与预警*

廖英雷

(西安科技大学 计算机科学与技术学院，陕西 西安 710054)

0 引言

2019年上半年全国煤矿企业共发生事故67起，其中因瓦斯事故死亡人数占比42%，可见瓦斯事故是煤炭安全生产的最大威胁[1]。通过对瓦斯数据的监测和异常数据的检测来预警危险，对煤矿的安全生产有重大意义。煤炭的采出必然破坏岩层的原始平衡状态而引起岩层运动，从而导致瓦斯涌出或突出，为生产带来风险[2]。在煤层产状不稳定的条件下，瓦斯突出点主要分布在煤层应力较集中且应力梯度变化较大部位[3]。工作面采掘机的工作会改变煤层的应力，从而导致瓦斯突出，在通风不变的情况下，随着时间增加瓦斯浓度也随之增加，会带来瓦斯浓度超限的风险。目前瓦斯传感器主要采用频率信号传输，仅能输出单一数据信息，无法掌握更多的运行信息。当传感器监测值异常时，只能依靠人工推断传感器运行状态[4]。

随着国内外学者专家对煤矿开采的瓦斯浓度数据分析，对数据的不确定性进行深入研究，发现井下瓦斯数据的变化深刻影响煤矿生产安全。周鑫[5]研究了基于分类的时间序列异常检测方法及特征属性降维方法，并应用于矿井瓦斯异常检测；彭泓[6]等采用再生核算法来进行RBF神经网络的训练，通过W12[a，b]空间插值逼近的方法，把RBF神经网络的训练转换为解线性方程组，从而准确地预测出了瓦斯突出；吴海波[7]等采用流回归机器学习算法与正态统计分布技术相结合的方法来建立瓦斯浓度流数据异常检测模型，实时判断流数据中的异常，提高了瓦斯风险评价时效；敖培[8]等基于改进的加权欧氏距离对瓦斯浓度异常数据进行处理，分析出设备异常数据、噪声数据和瓦斯突出孤立点数据。韩磊[9]通过建立瓦斯涌出量混沌预测数学模型，根据瓦斯浓度预测结果及其预测区间进行预警阈值计算，并对其对应的预警等级进行划分，完成预警信息。基于分类的瓦斯浓度异常值检测随着监测时间的增加数据的累计，会造成该算法的不稳定，不能更准确的分别异常数据。而神经网络的算法有较好的识别准确率，但算法复杂，数据量较大时需要对数据进行长时间的分析；利用损失函数易于计算的线性算法做成流式回归机器学习算法有一定的局限性；基于改进的加权欧氏距离的算法随着新数据的增长需要重新计算欧氏距离；建立瓦斯涌出量混沌预测数学模型的方法由于参与计算的数据比较多，实时性较差。为此，使用逻辑回归模型对时间序列瓦斯浓度数据进行检测与分析，判断出风险所在，降低对人工分析的依赖，为排除风险提供可靠的依据。判断异常数据，能在时间复杂度相对低的情况下较为准确的分析出异常数据，且有一定的实时性。

1 瓦斯相关数据预处理

1.1 试验数据采集

采集范围：试验数据来自陕北某矿的瓦斯浓度数据，经勘探该矿区煤层处于瓦斯风化带中，瓦斯含量在0．05～6.49 mL/g·r；煤层原始瓦斯压力为1.2～1.59 MPa；煤层瓦斯相对含量为9.32～11.73 m3/t；透气性系数11.49 m2/MPa2·d；该区煤层含气量高，煤层透气性好，瓦斯压力大[10]。采煤区在进行勘探后，会进行6～12个月的预抽采以降低煤层的瓦斯含量，当抽采达标后进行生产。该数据是实时监测的采煤工作面上隅角瓦斯浓度数据，数据间隔取1 min，瓦斯浓度数据范围是0%～100%，并且在0%～5%浓度范围内其测量误差小于±0.06%。采煤工作面上隅角瓦斯浓度传感器T0分布，如图1所示。

图1 传感器位置分布

采集方法：风由进风巷吹到工作面，带走工作面的瓦斯，上隅角的传感器对气体进行检测，带瓦斯空气随着回风巷排到通风巷道，因此上隅角的瓦斯浓度数据能反映工作面瓦斯浓度的变化。根据国家和矿区规章制度，矿区瓦斯浓度传感器装备数量和报警浓度的规则制度见表1[11]。如图2所示，数据组1来自该矿区的803工作面7 d的瓦斯浓度数据，用作训练数据，采集间隔为1 min，其中有异常数值31个，监测数据最大浓度2.11%，最小值为0.01%，平均值为0.253%，标准差为0.104%，大部分数据在瓦斯浓度0%～1%之间进行有规律的波动。另有数据组2来自工作面采集8 h的数据作为测试数据如图3所示，采集间隔为1 min，最大浓度为0.58%，最小浓度为0.08%，均值为0.212%，标准偏差为0.117%，数据集随时间进行规律波动。

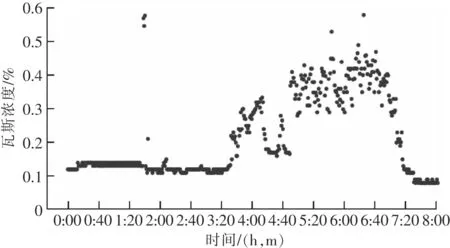
图3 8 h工作面瓦斯浓度随时间变化散点图

图2 1周工作面瓦斯浓度变化散点图

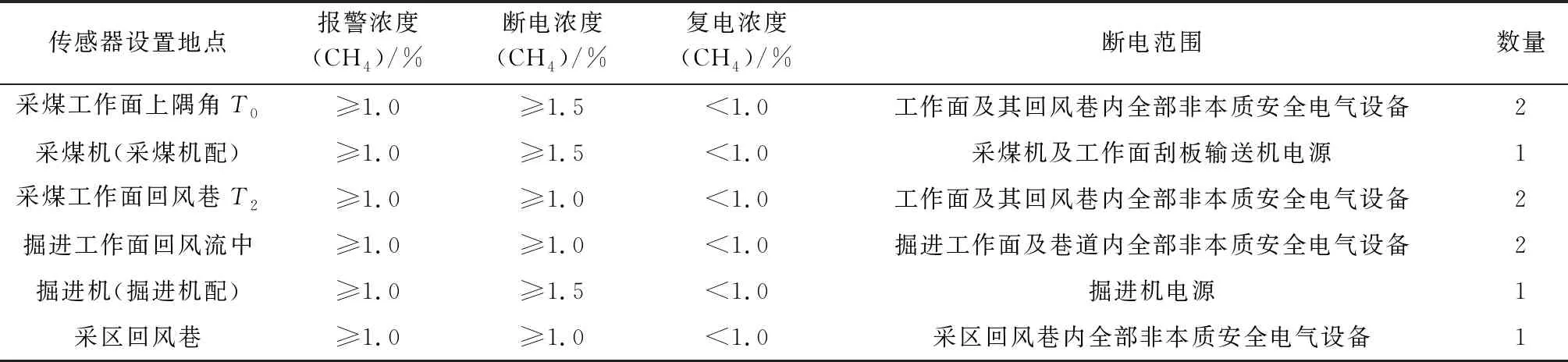
表1 瓦斯浓度传感器装备数量

数据处理的必要性：井下瓦斯浓度的情况仅依据国家和矿区的规章制度来判断是否报警还是断电是有弊端的，当采掘工作面没有开始工作处于检修状态时，采集到的瓦斯数据大部分在0.0%～0.2%之间，此时检测到异常数据若为0.6%未超过1.0%的报警上限，监测监控系统选择不报警是有可能带来风险的。因此，要对采集到的瓦斯浓度数据进行即时有效的分析，规避井下瓦斯突出等风险因素。

1.2 数据的分析与预处理

缺失数据插补：煤矿的原始数据一般包含异常数据(噪声)，因此在用机器学习的办法进行数据分析和建模前，就要对异常数据进行预处理来适应模型。异常数据包括：缺失值、异常值、不一致的值、重复数据及含有特殊符号(如#、￥、*等)的数据。本次研究瓦斯浓度的异常数据，只需将瓦斯监测设备的故障、通信信号被干扰等原因采集到的缺失值(如null)，浓度数据为100%或者0%及含有特殊符号(如#、￥、*等)的数据进行处理，对这些数据采用插补的办法进行处理，常用的方法见表2。

表2 常用的缺失数据插补方法

回归模型分析：以间隔1 min采集到一周瓦斯浓度数据有9 360个，缺失值为14个，缺失值较少且瓦斯数据会随时间变化添加新数据。当设备故障时缺失数据是连续的，对该数据用回归方法插补进行补差，回归方法插补根据已有数据和与其有关的其他变量数据建立拟合模型来预测是无偏估计，虽容易忽视随机误差，但较为适合具有线性关系的数据。瓦斯数据的P-P图如图4所示，点的分布接近直线y=x线进行分布且比较对称；在如图5所示，点分布于y=0两侧且对称，可看出瓦斯浓度数据分布也符合Logistics回归模型。

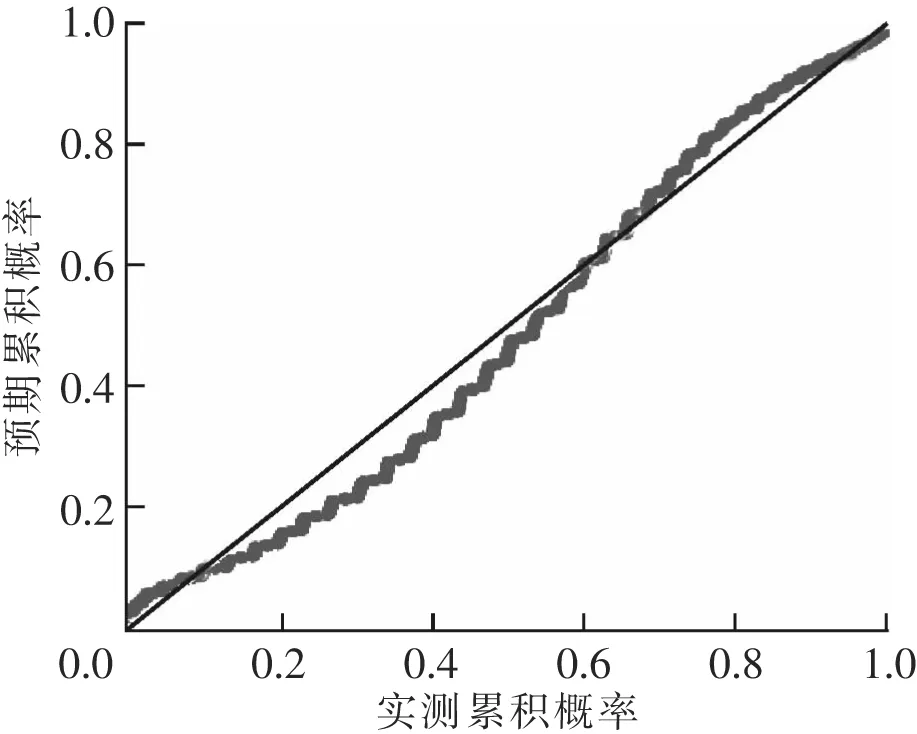
图4 瓦斯浓度Logistics P-P图

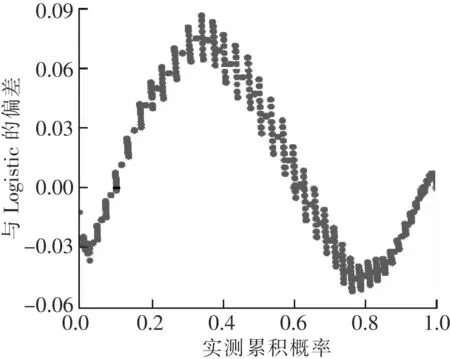
图5 瓦斯浓度Logistics去趋势P-P图

2 逻辑回归分析

2.1 逻辑回归分析的作用

逻辑回归介绍：逻辑回归(Logistic Regression)是一种用于解决二分类(0/1分类)问题的机器学习方法，用于估计某种事物的可能性。逻辑回归(Logistic Regression)是广义线性模型(generalized linear model)其中一种。该模型通过假设因变量y服从伯努利分布，自变量x与因变量y存在线性关系，利用Sigmoid函数处理非线性数据，从而解决二分类问题。

逻辑回归分析的作用：当工作面的瓦斯浓度数据异常时但未达到报警浓度为1%的阈值，通过逻辑回归模型对数据进行分析，不仅能检测出异常数据还可提前数分钟进行预警从而帮助矿区提前排除风险或者调整工作面刀头速度保证安全生产。

2.2 逻辑回归模型的建立

建立过程：逻辑回归模型的建立需要以下过程，首先要建立代价函数，然后通过优化方法迭代求解出最优模型参数，最后测试验证得到逻辑回归模型。

建立代价函数：瓦斯浓度数据集t包含t1，t2，…,tn，这些数据赋予一个权值w，带有权值的瓦斯浓度数据wTt计算见式(1)

(1)

定义f(t)=wT·t，定义函数g(i)=Sigmiod(i)见式(2)，Sigmiod函数其函数图像如图6所示，值域是[0，1]。

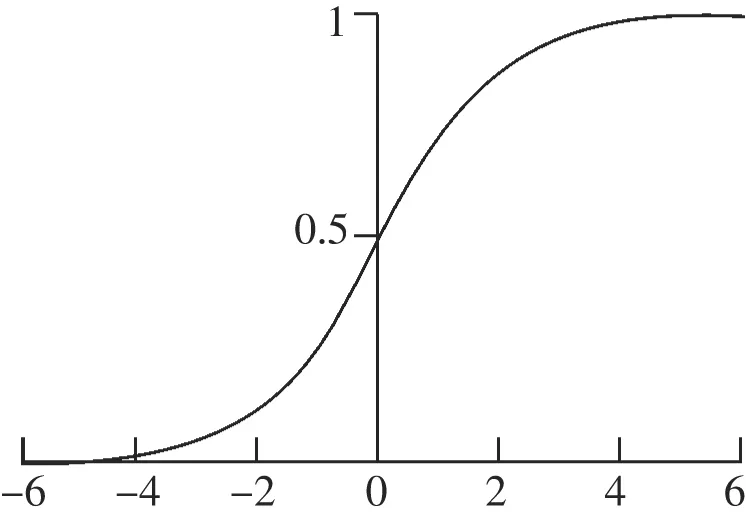
图6 Sigmiod函数图像

(2)

样本数据正反类划分：用函数g(i)映射f(t)，当f(t)≥ 0.5时，表示t被分到正类，当f(t)<0.5时，表示t分到反类，f(t)的数值在[0，1]之间可看为概率。此时瓦斯浓度数据已经能被划分出2类，分类函数记为P(y|t)，也可记为P(y|x)。定义h(x)表示预测出的样本数据是正类的概率，则反类的概率为1-h(x)，定义让步比为正类和反类的比值，取对数计算见式(3)，并用对数求解得式(4)

(3)

(4)

模型的预测函数：将带有权值的瓦斯浓度数据代入函数f(x)进行非线性求和得h(x)，如图7所示，用g(i)函数映射f(x)得到h(x)，即h(x)→g(f(x))，代入瓦斯浓度数据，对进行加权求和与非线性输出得出h(x)，如图8所示。函数h(x)有Sigmiod函数的特性为模型的预测函数。

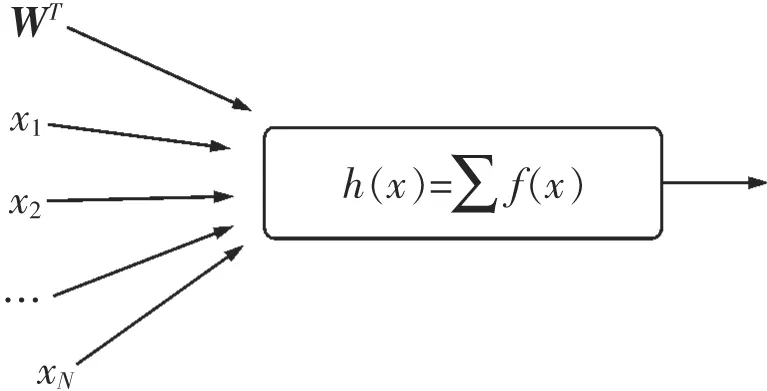
图7 线性模型加权和

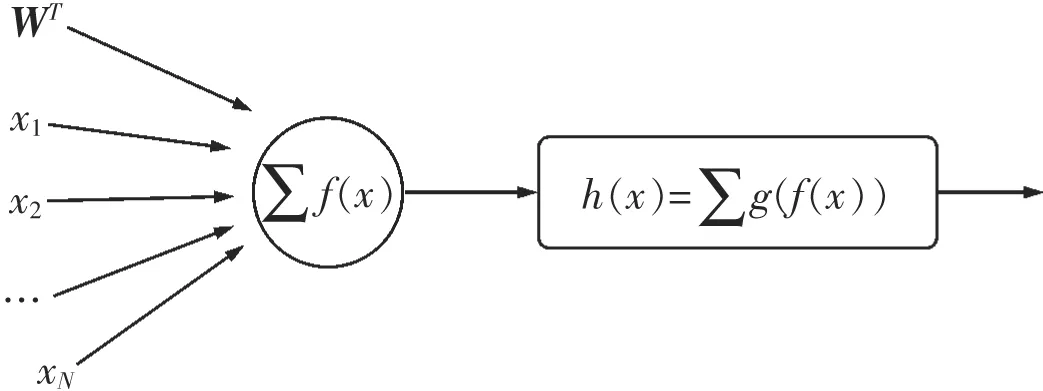
图8 加权和非线性输出

瓦斯浓度数据计算：瓦斯浓度数据是已经知结果，需要寻找使得该结果出现的概率最大的条件，构造函数选择似然函数，似然函数是统计模型函数中参数的函数。利用瓦斯浓度数据进行参数估列。建立似然函数L(w)，每个样本互相独立，n个瓦斯浓度数据样本出现的似然度为式(5)

(5)

取函数L(w)的自然对数得l(w)，化简计算见式(6)，为损失函数Loss函数与f(x)的关系。

(6)

对损失函数进行最优化，得到对应的f(x)，以此找回归因子W，对参数W求偏导数并化简得式(7)

(7)

以上步骤得到f(x)，知l(w)为损失函数，l(w)求偏导数，得梯度上升公式(8)。a表示每次迭代上升的幅度，利用瓦斯浓度数据与时间的数据来寻找回归因子W逼近最合理的参数列表。

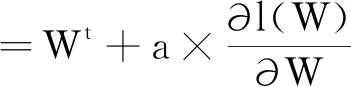
(8)

若将w=w+a×x.T×(y-h(x))定义为梯度上升公式，其随机梯度上升为w=w+a×x[j，：].T×(y[j，：]-h(x))，是从所有的数据样本矩阵x和y样本中随机选出的一个数据点来计算梯度并更新参数，有新的样本数据增加时只需要对模型进行增量式更新。

2.3 瓦斯浓度数据训练及分析

瓦斯浓度数据训练：瓦斯浓度数据的训练数据集D的属性有3个：C，T，V。瓦斯浓度数据集合为C中有数据C1、C2…，Cn；时间T以分钟为单位；该时刻瓦斯浓度数据是否为异常值V(是异常数据为1不是为0)。通过已经监测出来的瓦斯浓度数据利用公式求出预测函数h(x)，求得拟合预测数据h(T)。训练数据中有异常数据n个，计算拟合预测值与实测值的相对差值di=|Ci-h(T)|，阈值Threshold按照Sigma原则取值。对比di与阈值的大小，当di大于阈值时则记该时刻瓦斯浓度数据为异常数据，检测出来的异常数据个数与n进行对比选择合适的Sigma。

瓦斯浓度数据分析：测试集需要分析的瓦斯浓度数据集的属性有S(测试集瓦斯浓度实测值)和T(时间)。利用训练出来的回归模型用于测试数据集，得到拟合回归数据h(T)，计算拟合预测值与实测值的相对差值dj=|Sj-h(T)，将数据的相对差值dj与模型阈值Threshold进行对比，当dj≤Threshold时，该M时刻的瓦斯数据为正常数据，当dj>Threshold时，此刻的瓦斯浓度数据为异常数据，需要进行预警。

3 试验与分析

3.1 阈值选取

数据统计：该数据来自陕北某矿的803综采工作面的回风隅瓦斯传感器采集间隔为1 min的7 d的瓦斯浓度数据作为训练数据。通过分析统计，该监测点最大浓度2.11%，最小值为0，平均值为0.253%，标准差为0.104%。对该瓦斯浓度数据的P-P图如图9所示，可以看出图中点的分布几乎符合y=x，则说明该数据符合正态分布。绘制瓦斯浓度数据的正态分布图如图10所示。

图10 瓦斯浓度正态分布

图9 瓦斯浓度数据正态P-P图

阈值确定：阈值需要根据Sigma原则进行取值，从正态分布图来看，(μ-σ，μ+σ)中的概率为0.652 6，其中μ近似于0.3，σ近似于0.1。阈值Threshold=μ+kσ(k=1，2，3)。对训练数据集用逻辑回归模型进行分析，得到结果如图11所示。其预测方程式为1/(0.166 666 666 666 666 7+4.967 385 168 684 82×0.999 959 195 617 732 7×x)，阈值Threshold=μ+kσ(k=1，2，3；μ=0.3%；σ=0.1%)。当k=1时，检测出异常数据31个；当k=2时，检测出异常数据28个；当k=3时，检测出17个异常数据。由于训练集的异常数据n=31，所以k=1时，阈值设为0.4%比较适合。

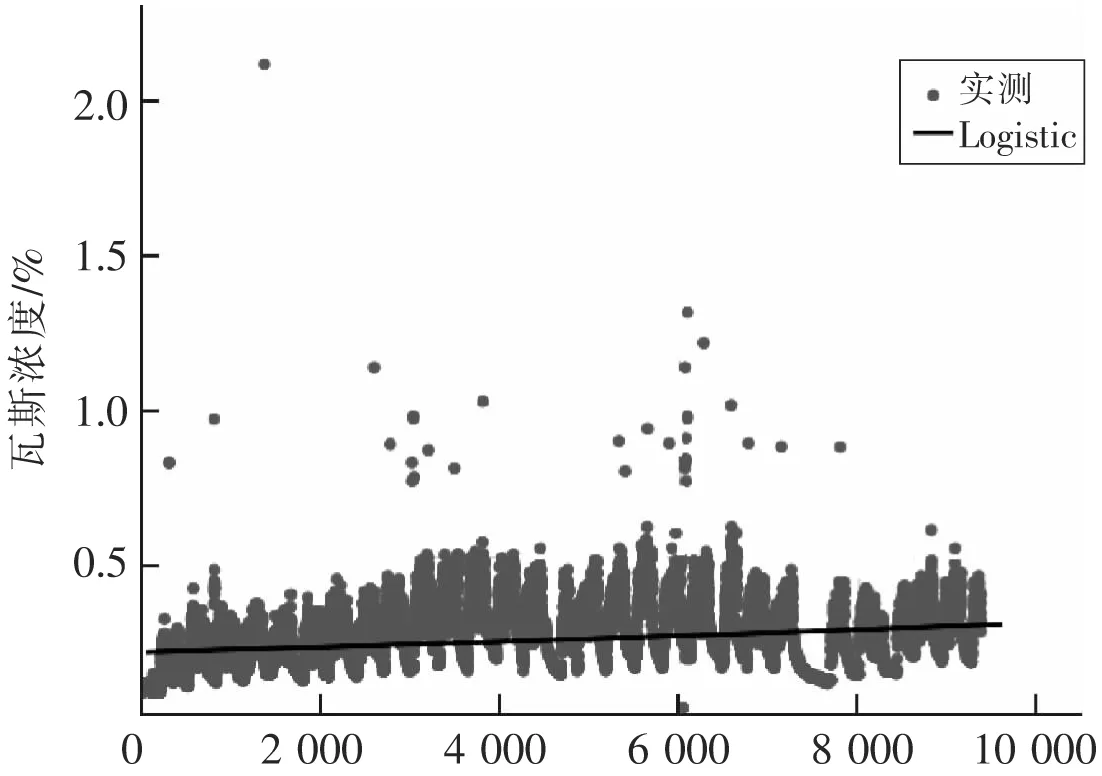
图11 训练数据进行逻辑回归预测

3.2 模型应用

测试结果：数据组2是在工作面连续采集8 h的瓦斯浓度数据，时间间隔为1 min，作为测试集数据，其中包含15个异常瓦斯浓度数据。该组数据统计范围有0.84%，最大值0.92%，最小值0.08%。用经过训练的Logistics回归模型对其进行分析，如图12所示，阈值取0.4%，预测出相应的瓦斯浓度数值并根据其与实测数据的相对距离来判断是否为异常数据。此组数据共检测出13个异常数据，准确率为0.867%。

图12 逻辑回归模型分析测试数据

异常数据分析：测试集数据情况特殊，在工作面进行检修时，上隅角传感器采集到数据中有异常数据，需要预警。但采煤机没有工作，煤层的应力结构没有遭到人为破坏[12]，因此瓦斯浓度异常数据的产生是由于地壳结构的变化导致瓦斯突出[13]。

4 结论

(1)逻辑回归模型中的随机梯度上升算法是一个在线学习的算法，能减少计算机资源的利用，保证系统的稳定。通过逻辑回归模型对瓦斯浓度的异常值进行检测，判断此时是否有异常情况发生，识别异常数据的正确率达85%以上，能够实现提前预警。

(2)利用一部分数据对逻辑回归模型进行分析，得到相关参数，样本数据随着时间的累加，通过不断检测异常数据的过程，该模型能得到越来越多较好的参数，使得模型对异常数据的检测会越来越准确。

(3)通过试验结论与数据分析，可以利用逻辑回归模型基于不同阈值的情况下，建立一个分级报警的瓦斯浓度异常值检测系统，有效识别未达到阈值上限的瓦斯数据是否存在异常状态，这对优化矿井瓦斯浓度的检测与预警提供了新方法。

本文写作过程中得到了王安虎博士、曹健博士的支持和帮助，在此深表感谢！