基于BAS算法优化的感应电机参数估计

金逸珲 吴滨 顾晓峰 张晓昕

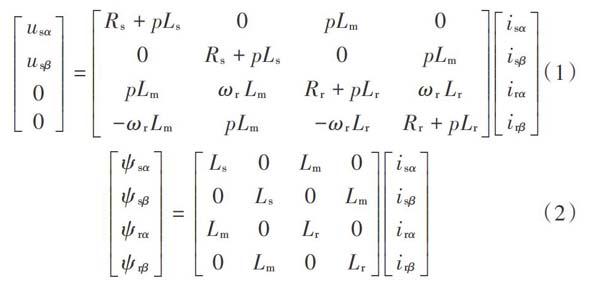
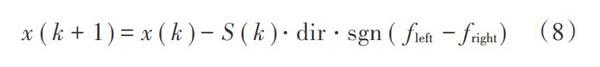
摘  要： 为了提高感应电机系统参数估计与状态监测的准确性和效率，针对感应电机非线性、强耦合、参数易时变的特性，引入带外部输入的非线性自回归（NARX）神经网络时序预测模型。针对传统NARX神经网络初值依赖和收敛速度慢的问题，利用天牛须搜索算法（BAS）对神经网络预测模型进行参数寻优，提高神经网络的收敛速度和预测精度。实验结果表明，该方法能够以较简单的网络结构高效、准确、稳定地预测估计电机参数。

关键词： 感应电机; NARX神经网络; 参数估计; 天牛须搜索算法; 收敛速度; 预测精度

中图分类号： TN98?34; TM346                     文献标识码： A                     文章编号： 1004?373X（2020）03?0112?04

Induction motor parameter estimation based on BAS algorithm optimization

JIN Yihui1， 2， WU Bin1， 2， GU Xiaofeng1， 2， ZHANG Xiaoxin1， 2

（1. Engineering Research Center of IoT Technology Applications （Ministry of Education）， Wuxi 214122， China;

2. Department of Electronic Engineering， Jiangnan University， Wuxi 214122， China）

Abstract： In order to improve the accuracy and efficiency of parameter estimation and condition monitoring of the induction motor system， a time series prediction model based on nonlinear autoregressive with exogenous input （NARX） is introduced in consideration of the characteristics of nonlinearity， strong coupling and time?varying parameters of the induction motor. To solve the problem of initial value dependence and slow convergence speed of traditional NARX neural network， the beetle antennae search （BAS） algorithm is adopted to optimize the parameters of the neural network prediction model and improve convergence rate and prediction accuracy of the neural network. The results of experiments show that the proposed method can predict and estimate the motor parameters efficiently， accurately and steadily with a simple network structure.

Keywords： induction motor; NARX neural network; parameter estimation; BAS algorithm; convergence rate; prediction accuracy

0  引  言

感應电机因其结构简单、维护方便、成本低廉、运行可靠等特点，被广泛应用于交通运输、工业生产、能源发电等领域。然而，在不少应用场景中，电机的工作环境往往比较恶劣，需要对其进行实时监测，保障系统的最优控制和可靠运行，才能保证系统的稳定性及安全性，并对可能出现的问题实现预警。因此，对电机系统进行状态监测，时刻掌握电机准确的运行参数，对电机系统的稳定运行、优化控制、故障预警等具有重要意义。

为了高效、准确地识别电机参数，研究人员提出了多种参数估计与监测方法[1?4]。通过安装辅助传感器能够快速获取电机的关键参数，但是对于复杂工况下的感应电机工作系统，传感器的安装和维护增加了驱动系统的复杂性，降低了系统的可靠性，同时增加了成本。因此，利用已有信号测量电机运行参数的无线传感器技术开始受到重视，其中，包括最小二乘法[5]、卡尔曼滤波[6]、模型参考自适应[7]等方法。不过，这些方法依赖于理想化的电机数学模型，实际运行中的电机系统各项参数易发生时变，这将直接影响算法的精度。

神经网络因能任意逼近连续非线性函数的特点而被广泛研究与应用，但传统BP神经网络[8]采用静态框架进行建模，难以准确描述感应电机这类多变量、非线性、强耦合系统的动态性能。描述系统动态性能的神经网络应具有可以反映系统动态特性和存储信息的能力，即要求网络中存在信息的延时与反馈。针对上述问题，本文引入带外部输入的非线性自回归（Nonlinear Autoregressive with exogenous input，NARX）[9]网络，结合天牛须搜索（Beetle Antennae Search，BAS）算法[10]优化网络权重和阈值，简化网络结构。结果表明，该方法能准确、稳定、动态地预测估计电机参数。

1  感应电机数学模型

感应电机在两相静止坐标系下的电压方程与磁链方程[11]可表示为：

式中：[u]为电压;[i]为电流;[ψ]为磁链;下标中的[s]，[r]分别代表定子、转子;[α]，[β]分别代表坐标系的两轴;[Ls]，[Lr]，[Lm]分别表示定子电感、转子电感和定转子间的互感;[R]为电阻;[p]为微分算子;[ωr]为转速，可由电压、电流表示为：

式中：[σ=L2m-LsLr];[u′sα=usα-Rsisα]。

电磁转矩与负载可表示为：

由上式可知，电机转速与定子的电压、电流及其他一些参数之间存在着复杂的非线性关系。给定电机的定子电压、电流和其他参数后，即可由式（3）进行转速估计。根据得到的转速信息，可以进一步估计电机的转矩负载等其他电气参数。由于电机参数受工况影响会发生时变，而参数的变化会直接影响预测结果，因此基于电机数学模型的参数估计精度难以保障。

2  基于BAS算法优化的NARX神经网络参数估计

2.1  NARX神经网络

NARX神经网络是一种基于时间序列的非线性动态循环网络，它由输入层、隐含层、输出层和时延反馈组成，其网络结构如图1所示。

NARX神经网络的输入、输出之间并不只是静态的映射关系，它在BP神经网络的基础上将网络输出通过延时节点反馈到输入端。由于延时节点存储了前几个时刻的输入、输出信息，因此，该网络模型具有良好的动态特性[9]。网络的动态行为可描述为：

式中：[y（t-1），y（t-2），…，y（t-n）]是输出延时项;[u（t-1），u（t-2），…，u（t-n）]是输入项;[y（t）]是网络预测估计值。当前输入与过去输出的反馈通过隐含层的权重与偏置计算回归量，进而通过非线性函数[fh]与线性函数[fo]估计预测值。

2.2  天牛须搜索算法

尽管NARX神经网络具有良好的动态特性，但其对初始权值的依赖影响了模型训练的稳定性，并且传统的神经网络训练算法收敛较慢。针对上述问题，文献[12]利用粒子群算法（PSO）优化NARX网络权值，对于一般问题的优化，粒子群算法具有速度快、精度高等优点，但是对于高维多参数问题，其计算速度与优化效果明显变差。为了提高NARX网络的收敛速度与精度，本文引入BAS算法对NARX网络进行参数寻优。

BAS算法是最近提出的一种类似于群体智能算法的仿生优化算法，它不需要知道目标函数的具体形式或梯度信息，就可以实现高效寻优。由于BAS算法只需要设置一个个体，所以相较于一般的多参数群智能算法，计算量低、速度快、易于实现，适用于工程应用。

BAS算法由天牛觅食原理启发而来：对于未知食物源，天牛通过头前两须接收到的食物气味强弱来觅食，根据两须气味强弱的差异改变前进方向，逐渐飞向目标，找到全局气味最强的点。BAS算法具体步骤如下：

1） 将在三维空间搜索的觅食行为引申到[n]维空间，对应[n]维优化问题。设置天牛中心位置为[x]，两须分别位于中心左右两边，设为[xleft]，[xright]，间距为[d]，其中，[x]，[xleft]，[xright]均为[n]维向量。

2） 设置天牛每前进一步之后的方向随机，也即右须指向左须的方向随机，避免陷入局部最优。生成一个[n]维单位随机向量，表示其右须指向左须的方向：

式中[rands（n，1）]表示生成[n]维随机向量，则左右两须的位置分别为：

式中：[x（k）]，[d（k）]分别表示第[k]次迭代时的中心位置与两须距离。

3） 根据当前所在位置与目标优化函数[f]计算两须相应的适应度值[fleft]，[fright]，以其大小关系确定下一步的前进方向：

式中[S（k）]表示第[k]次迭代時的前进步长。

根据以上三步迭代直到满足计算终止条件，所得到的中心位置[x]即为目标函数的最优解。

2.3  基于BAS优化的NARX网络训练流程

初始化NARX网络结构与权值，将权值参数的集合设为BAS算法搜索空间，将网络误差函数MSE设为目标优化函数，按照2.2节的步骤迭代即可得到全局最优解。基于BAS算法采用固定步长搜索最优解;文献[13]在每次迭代时对步长乘以衰减系数来提高搜索精度。对于拥有多个参数的NARX网络，各参数差值较大，数值大小也不与目标函数的适应度值直接相关。固定步长无法兼顾每个参数，易使算法早熟收敛;带有衰减系数的变步长能细化参数搜索，但是当迭代次数较高后，步长在衰减系数的影响下会变得过小而无法改变参数。

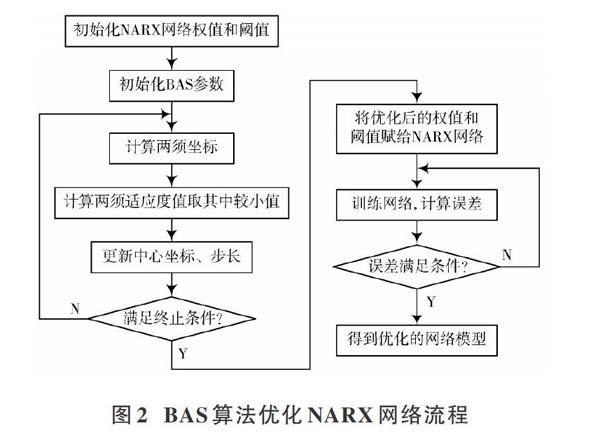
本文中，对于有[n]个参数的目标函数，根据初始化参数设置对应的初始步长[Si]，最小步长[S0i]和衰减系数[wi]，其中，[i=1，2，…，n]。迭代过程中，如果当前步长能使适应度值减小，表明当前步长有效，则保持该步长不变。基于BAS算法优化的NARX网络流程如图2所示。

3  仿真验证

为了验证上述算法对电机参数预测的性能，采用Matlab/Simulink对感应电机系统建立仿真模型，并对NARX神经网络和BAS算法进行仿真实验。仿真中所用感应电机参数如下：额定电压[U=]380 V，额定电流[I=]10 A，额定频率[f=]50 Hz，定子电阻[Rs=]1.41 Ω，转子电阻[Rr=]1.39 Ω，定子电感[Ls=]0.178 0 H，转子电感[Lr=]0.178 0 H，互感[Lm=]0.172 2 H，转子极对数[np=]2，转动惯量[J=]0.013 1 kg·m2。

3.1  数据预处理

利用定子电压与电流作为训练样本，电机模型产生的转速作为训练目标，训练NARX神经网络，可以得到转速估计模型。由于电机参数的时变性，真正工况下的输入信号频率必然会有所波动，这将减弱网络预测估计的鲁棒性，造成恒定输出在频率上的失调。本文将更为稳定的电压、电流有效值及与转速高度相关的瞬时功率作为参考，利用瞬时无功功率和转速信息训练神经网络，提高训练速度和稳定性，同时简化网络结构。

3.2  算法验证

本文对NARX，PSO?NARX，BAS?NARX三种网络训练效果进行比较，以确定训练模型，其中，PSO算法采用文献[14]中带惯性权重与变异因子的粒子群算法。训练样本采用电机空载启动的前0.4 s输入输出信号，设置最大迭代次数1 000次，误差评价标准为均方误差MSE，分别训练50次取平均值。训练结果如图3所示。

从图3可以看出，NARX与PSO?NARX网络初期收敛速度较快，传统NARX网络在均方误差达到0.01后，收敛速度迅速下降;PSO算法收敛曲线有明显的平台阶段，表明算法陷入局部最优，只有依靠变异因子跳出局部最优时才能进一步收敛;BAS算法虽然初期收敛速度较慢，但是能以稳定的速度收敛到全局最优解，得到精度最好的网络模型，证明了BAS算法对NARX网络的参数寻优是有效的。

3.3  仿真分析

利用训练得到的神经网络模型对电机参数进行预测估计。为了验证所得模型对变化转速的跟踪性能，进行转速阶跃工况的仿真。设置电机初始转速为600 r/min，0.4 s时转速阶跃至1 400 r/min，0.7 s时阶跃至1 000 r/min。

转速阶跃工况的仿真结果如图4所示。可以看出，网络模型能够很好地跟踪转速变化，尽管在转速阶跃变化时会产生相应的超调量，但能快速到达目标值。转速跟踪的误差如图5所示。可以看出，模型估计值在短暂震荡后恢复稳态，建立时间小于0.04 s，稳态误差小于0.6 r/min。

为了验证所得模型对负载变化的应对能力，进行了负载阶跃工况的仿真。设置电机初始负载为2 N·m，0.4 s时转速阶跃至10 N·m，0.7 s时阶跃至6 N·m。

负载阶跃工况的仿真结果如图6所示。可以看出，电机转速随着负载的增大而减小，随着负载的减小而增大，网络模型都能快速响应负载变化，稳定估计转速。负载变化时的速度估计误差如图7所示。可以看出，启动阶段最大超调量约为1 r/min，运行阶段负载变化时最大误差为0.1 r/min，证明了模型的稳定性和准确性。

图8为利用估计转速进一步得到的负载估计。结果表明，负载估计直接受到电机转速的影响，会由于转速突变而产生相应的阶跃变化，但能在极短时间内恢复稳定，得到准确的估计值。由此证明本模型具有良好的响应速度和估计精度，同时具有良好的泛用性。

4  结  语

针对采用静态框架的传统神经网络难以准确描述感应电机这类多变量、非线性、强耦合系统动态性能的问题，本文引入NARX神经网络模型，通过优化网络的输入参数简化网络结构，利用BAS算法优化神经网络的训练权值，加快网络收敛。结果表明，本文方法能够以较简单的网络模型、较少的训练次数和较短的训练时间，得到高效、动态、准确、稳定的预测模型，实现对感应电机的参数估计。

参考文献

[1] 雷杨，谷立臣，刘沛津.电力拖动设备三相电信号实时监测系统开发[J].机械科学与技术，2013，32（8）：1149?1152.

[2] 王晨辉，郭英军，仝浩，等.基于ARM和Linux的嵌入式异步电机监测系统[J].仪表技术与传感器，2011（11）：68?70.

[3] PATIL R R， DATE T N， KUSHARE B E. ZigBee based parameters monitoring system for induction motor [C]// 2014 IEEE Students′ Conference on Electrical， Electronics and Computer Science. Bhopal： IEEE， 2014： 1?6.

[4] 刘朝华，李小花，张红强，等.基于并行动态学习型免疫算法的永磁同步电机状态监测[J].自动化学报，2015，41（7）：1283?1294.

[5] AHN H J， LEE D M. A new bumpless rotor?flux position estimation scheme for vector?controlled washing machine [J]. IEEE transactions on industrial informatics， 2016， 12（2）： 466?473.

[6] YIN Z G， ZHAO C， ZHONG Y R， et al. Research on robust performance of speed?sensorless vector control for the induction motor using an interfacing multiple?model extended Kalman filter [J]. IEEE transactions on power electronics， 2014， 29（6）： 3011?3019.

[7] ZBEDE Y B， GADOUE S M， ATKINSON D J. Model predictive MRAS estimator for sensorless induction motor drives [J]. IEEE transactions on industrial electronics， 2016， 63（6）： 3511?3521.

[8] 刘云飞，李兵，姚明林.基于PSO优化的模糊神经网络的直接转矩控制[J].现代电子技术，2018，41（19）：117?120.

[9] ISMEAL G A， KYSLAN K， FED?K V. DC motor identification based on recurrent neural networks [C]// Proceedings of the 16th International Conference on Mechatronics?Mechatronika. Brno： IEEE， 2014： 701?705.

[10] ZHU Z， ZHANG Z， MAN W， et al. A new beetle antennae search algorithm for multi?objective energy management in microgrid [C]// 2018 13th IEEE Conference on Industrial Electronics and Applications. Wuhan： IEEE， 2018： 1599?1603.

[11] 顾海勤，杨奕，张蔚，等.[αβ]?[dq]?0坐标系下高压电机起动特性的分析[J].现代电子技术，2018，41（17）：116?118.

[12] MOHAMAD M S A， YASSIN I M， ZABIDI A， et al. Compa?rison between PSO and OLS for NARX parameter estimation of a DC motor [C]// 2013 IEEE Symposium on Industrial Electronics and Applications. Kuching： IEEE， 2013： 27?32.

[13] 邵良杉，韩瑞达.基于天牛须搜索的花朵授粉算法[J].计算机工程与应用，2018，54（18）：188?194.

[14] 李琳，张栋栋，沙林秀，等.基于粒子群算法的钻进参数多目标优化[J].现代电子技术，2014，37（10）：24?27.