自重作用下吹填土地基的大变形固结分析

邱长林，于博文，闫澍旺，纪玉诚

（天津大学 建筑工程学院，天津 300072）

引 言

天津等沿海城市的人工吹填造地，其主要材料为吹填泥浆等超软土。由于吹填泥浆含水率高、强度低，需要对吹填地基预处理后再通过真空预压等方式加固。预处理的一般做法是让吹填地基在自然风干的条件下自重固结。本课题组通过试验发现，在吹填土自重固结过程中，自然风干的方法由于在表层形成一密实的硬壳层而阻碍了下部土体的固结，而如果在表层保持一定厚度的覆水将不会形成硬壳层，从而将有可能使整个吹填土地基含水量降低更快。为了评价这种预处理方法的效果并为设计提供依据，迫切需要建立吹填土地基在自重作用下的固结理论。

由于吹填土孔隙比大、压缩性高，吹填土地基在自重作用下固结变形非常大，同时泥面不断下降也有效减小了吹填地基中超孔隙水的渗透路径，所以吹填土地基的变形是一个大变形固结问题，需要采用大变形固结理论。目前的大变形固结理论一般可以划分为两种[1]，即 Gibson等[2-4]发展的一维大变形固结理论和Carter引进的、建立在非线性连续介质力学理论基础之上的大变形固结理论[5-11]。其中，非线性连续介质力学大变形固结理论虽然理论上比较严谨、扩展性强，但是该理论的固结方程形式复杂，工程应用上受到一定的限制，而 Gibson提出的一维大变形固结理论形式简单、物理意义明确，且经过长期深入的研究，已形成了较为完整的理论体系。但是该理论以孔隙比e为场变量，无法与传统 Terzaghi固结理论及 Biot固结理论进行衔接，不便于在这几种理论之间进行比较，且该理论一般采用常规固结压力作用下的固结特性，这和吹填土体在自重固结过程中应力较小的特性不符合。

目前对冲填土自重固结问题进行的研究非常少[12]，其设计也主要采用小变形理论的Terzaghi固结理论。为此，本文通过室内试验研究吹填土在小固结压力作用下的压缩特性，在Gibson理论的基础上，建立以超孔隙水压力为场变量的大变形固结方程，并通过模型试验对计算结果进行验证，以期能为吹填土地基的设计及寻求加快其自重固结的途径提供理论依据。

1 吹填土压缩特性

1.1 吹填土小荷载作用下的压缩试验

为了研究吹填土在小固结压力作用下的固结特性，需对常规固结仪进行改制，使其固结压力通过在改制的加压上盖上直接添加砝码的方法施加，从而可以对土体施加小数值的固结压力。

试验所用土样取自天津港，其液限为46 %，塑限为23 %，塑性指数为23。土样的制作采用土膏法，初始含水率分别为88 %、96 %和117 %。

试验采用一个土样施加不同等级固结压力的试验方法，荷载等级为2.5 kPa、3.5 kPa、4.5 kPa、6.5 kPa、8.5 kPa、10.5 kPa、15.6 kPa和 20.7 kPa等。变形稳定的标准为每小时压缩量小于0.01 mm。

1.2 试验结果分析

小固结压力作用下的固结试验得到的孔隙比和固结压力之间的关系如图1所示。从图中可以看出，吹填土在小固结压力作用下的压缩特性和常规固结压力作用下的固结特性不同。当固结压力小于10.5 kPa时，土体的孔隙比和固结压力之间并不存在一一对应关系，而是和初始含水率有关，即含水率越大，在相同固结压力作用下的孔隙比也越大。随着固结压力的增加，不同初始含水率土样的孔隙比之间差值逐渐减小。当固结压力超过10.5 kPa后，不同初始含水率的土体的孔隙比和固结压力之间存在一一对应的关系，即和一般土体的固结特性相同。该结果表明，在小固结压力作用下，吹填土存在一个临界压力，只有当固结压力超过该临界压力后，它的孔隙比和有效应力之间才存在一一对应关系，而在此压力之前孔隙比和固结压力的关系与初始含水率有关。在本试验中，临界压力为10.5 kPa。

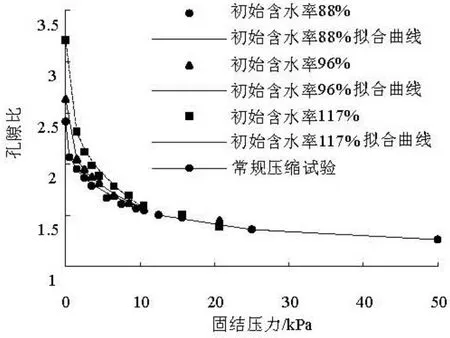
图1 吹填土压缩试验曲线

上述试验结果表明，吹填土体的固结压力和孔隙比之间的关系可以分为两段，即：

式中：e为孔隙比；σ′为固结应力；e0为初始孔隙比；σ*和e*分别为临界压力和该压力所对应的孔隙比；Cc为压缩指数；N为拟合参数。

图1中给出了本次试验三个土样在0～σ*范围内的拟合结果，其中N为 0.307，e*为 1.57，σ*为10.5 kPa，拟合结果和试验结果非常接近。因此有：

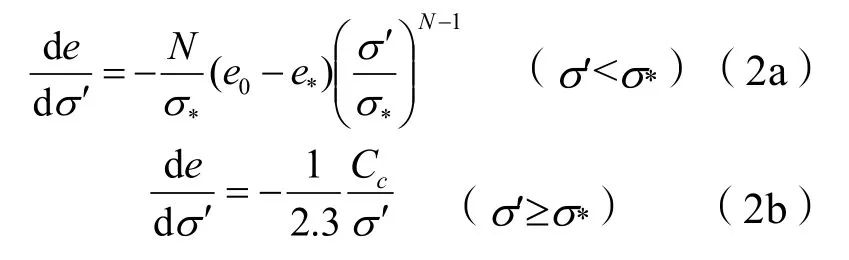
2 吹填土一维大变形固结理论

2.1 坐标系

在初始坐标系，即拉格朗日坐标系中，饱和软黏土地基的初始坐标状态如图2（a）所示。在该坐标系中，地基表面为a=a0，不可压缩层顶面为a=0。在该地基的坐标位置为a处取一微分体A0B0C0D0，其厚度为da，面积为1，孔隙比为e0。该地基在自重作用下固结，经过时间t后该地基在流动坐标中的状态如图2（b）所示。在该坐标系中，地基厚度变为z(a0,t)，选取的微分体变为 ABCD，其坐标位置为z(a,t)，厚度为dz，孔隙比为e，面积仍为1。根据微分体范围内土颗粒重量在变形前和变形后相同的条件，可以得到：

图2 固结理论坐标系

2.2 大变形固结方程

假定土体饱和，土颗粒和水不可压缩，土体的压缩和水的渗流只在竖向，且水和土颗粒的移动速度之差满足达西定律，根据饱和土体的变形连续条件可以得到在流动坐标系下土体的固结方程为：

式中：u为超孔隙水压力；γw为水的重度；k为渗透系数。

将式（3）代入式（4），可以得到在拉格朗日坐标系下的固结方程为：

对于图2所示的地基，如果泥面保持在水位线以下，则根据有效应力原理可知，流动坐标系中位置为z处的有效应力为：

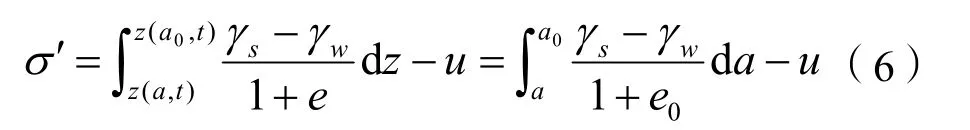
式中：γs为土颗粒的重度。

将式（6）代入式（5），可以得到：

式（7）即为拉格朗日坐标系下以超孔隙水压力u为场变量的固结方程。

对于图2所示的吹填土地基的重力固结问题，在初始坐标系下其边界条件和初始条件分别为：

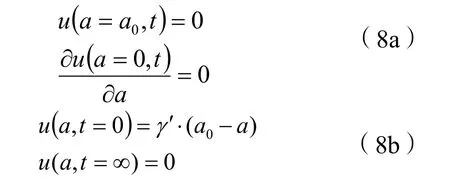
3 模型试验及理论分析结果

3.1 模型试验

为了研究表层有覆水情况下吹填泥浆在自重作用下的固结沉降过程。试验用的模型槽为一1.5 m×1.5 m×1.5 m的铁槽。试验用的吹填土液限为44 %，塑限为27 %。吹填泥面初始的高度为1.35 m，平均含水量为180 %。

泥浆吹填后静置，不经外界干扰，凭其自然固结，只是在试验过程中将表层的水抽出一部分。因此，在固结过程中吹填泥浆表层一直有水覆盖。在此过程中测量吹填泥浆表面的固结沉降量，直至泥面的沉降达到稳定。试验时间约持续1年。

3.2 理论分析模型

本研究通过有限元方法求解式（7）及式（8a）、式（8b）来模拟分析上述模型试验，其中，土体的比重取为 2.74，e0为 4.9，e*为 1.3，σ*为 10.5 kPa，N为0.2。

吹填土的渗透系数采用指数模型，即：

式中：k为渗透系数；k0和A为与土体塑性指数相关的拟合系数。根据渗透试验结果，k0取为1.7×10-7cm/s，A为 1。

为了比较，本分析同时采用常规设计中的Terzaghi固结理论对该模型进行了固结分析，固结系数的取值为地基中间位置处在固结结束时应力状态所对应的固结系数，即为0.0586 m2/Month。

3.3 分析结果

1）模型计算和试验的沉降结果对比

泥面固结沉降随时间变化的计算和试验实测结果如图3所示。图3表明，泥面在固结开始时沉降速度很大，随着时间的增加，沉降速度逐渐减小，计算结果在18.5个月时完全达到稳定值，最终沉降为 0.56 m。从图中可以看出，实测的最终沉降为0.62 m，试验结果和计算结果基本吻合，证明本计算结果的可靠性。

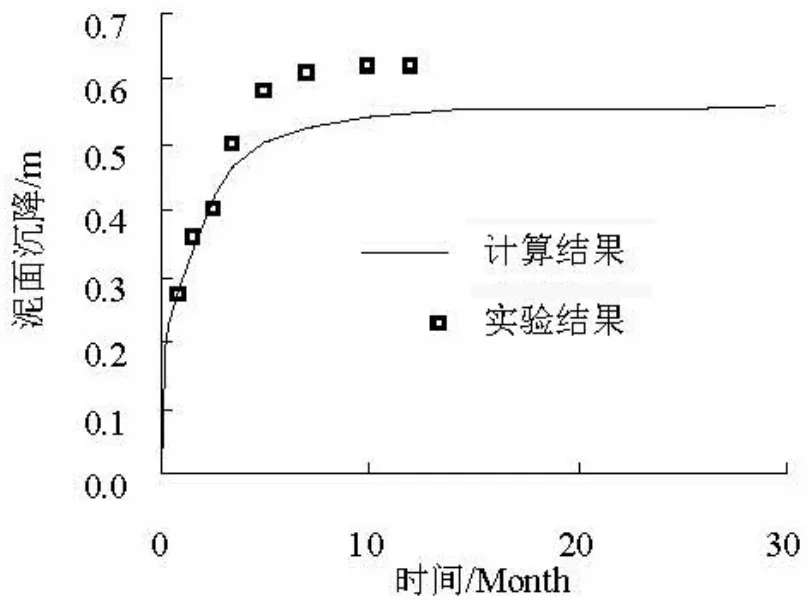
图3 泥面沉降变化

2）超孔隙水压力

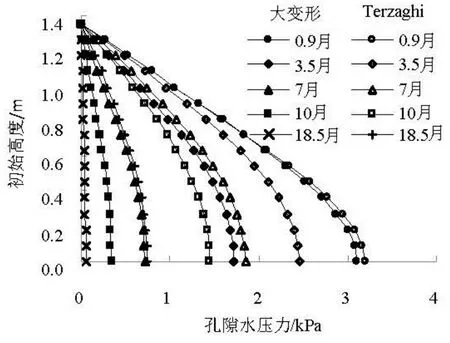
图4 孔隙水压力消散曲线

新吹填地基由于没有经历任何固结过程，其初始超孔隙水压力沿高度的分布为一条直线，该直线的斜率为泥浆的有效重度。随着固结时间的增加，地基中的超孔隙水压力不断消散，图4为不同初始高度处超孔隙水压力随时间的分布。该结果表明，在泥面的顶部，超孔隙水压力保持为 0，而泥面下的土体的超孔隙水压力由于土体的固结而逐渐消散减小。从图中可以看出，在相同的固结时间里，下部土体的超孔隙水压力消散值大于上部土体的消散值，特别是地基底部的超孔隙水压力降低值为最大，因此地基中超孔隙水压力沿初始高度的分布曲线向内弯曲。随着固结时间的增加，底部的超孔隙水压力消散速度开始变慢，最后完全消散为 0。图中数据表明，在18.5个月以后，地基的超孔隙水压力基本消散完毕。

图4同时绘制了常规Terzaghi固结理论计算得到的超孔隙水压力分布。从图中可以看出，当固结时间分别为0.9个月、7个月和18.5个月时，大变形固结理论计算得到地基底部的超孔隙水压力分别为3.11 kPa、0.71 kPa和0.05 kPa，而Terzaghi固结理论计算得到的超孔隙水压力分别为3.20 kPa、1.84 kPa和0.74 kPa。这表明，大变形固结理论计算得到的超孔隙水压力消散的速度远大于Terzaghi固结理论计算的结果。

3）固结度

图5为分别根据泥面位移和超孔隙水压力分布计算得到的平均固结度随时间的变化过程。从图中可以看出，一维大变形固结理论采用这两种方法计算得到的固结度并不相同，采用位移表示的固结度要远大于采用超孔隙水压力计算得到的固结度，如当固结时间分别为0.9个月、7个月和18.5个月时，采用位移表示的固结度分别为 50.9 %、94.9 %和99.7 %，而采用超孔隙水压力计算得到的固结度分别为7.8 %、78.2 %和98.5 %。这是由于土体的压缩系数是一个不断变化的参数，土体在固结的初始阶段，由于土体的孔隙水压力大，有效应力小，所对应的压缩系数大，在消散相同的孔隙水情况下压缩变形大；随着超孔隙水压力的消散，有效应力不断增加，压缩系数不断减小，在消散相同的孔隙水情况下压缩变形量逐渐减小。

图5 固结度比较

结果表明，吹填土在自重作用下的固结过程可以分为两个阶段。在开始阶段，即对应于位移固结曲线中的7个月以前和超孔隙水压力固结曲线的14个月以前，固结速度非常快。在随后的固结过程中，地基的固结速度则非常缓慢。

从图5由Terzaghi固结理论[13]计算得到的固结度变化曲线可以看出，Terzaghi固结理论计算得到的固结度远小于大变形固结理论计算得到的结果。因此，Terzaghi固结理论将严重低估吹填泥浆地基的固结速度。

如果以不同位置处的超孔隙水压力消散程度为该位置处的固结度，则可以得到不同高度处的固结度如图6所示。从图中可以看出，固结时间相同时，土体的固结度随着高度的增加而减少，即底部土体的固结速度大于上部土体的固结速度。这个规律说明，虽然地基的排水面在泥面，但是在地基固结的初始阶段，地基底部的超孔隙水压力消散的速度较快，而顶部的超孔隙水压力消散较慢。这主要是由于顶部的超孔隙水消散的比较小，因此其孔隙比变化小，渗透系数一直比较大，这有利于底部土体超孔隙水压力的消散。

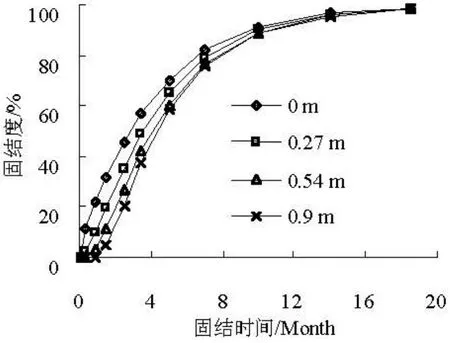
图6 不同高度处的固结度

4 结 语

通过吹填土的室内小围压固结试验，建立了吹填土的孔隙比和固结压力之间的关系，并建立了以超孔隙水压力为变量的一维大变形固结方程。通过对模型试验进行一维大变形固结理论分析，得到如下结论：

1）吹填土体在小荷载作用下的压缩特性和常规荷载作用下的压缩特性不同。在小荷载作用下，吹填土的压缩曲线存在一个临界应力，当固结压力小于该应力时，孔隙比和有效应力之间的关系与土体的初始孔隙比有关，只有大于该临界应力时孔隙比和固结压力的对数之间才是一一对应的线性关系。

2）吹填土自重固结过程中，当泥浆保持在水位以下时，底部的超孔隙水压力和孔隙比降低较快，固结过程中上部土体的渗透系数大于下部的渗透系数，这有利于吹填土体中孔隙水向泥面排出。因此，固结时间相同时，底部土体的固结度比上部土体的固结度大。

3）按沉降计算得到的固结度大于按超孔隙水压力消散程度计算得到的固结度。大变形固结理论计算得到的孔隙水压力消散速度和固结度都远大于常规Terzaghi固结理论计算得到的结果。因此，用Terzaghi固结理论计算吹填土在自重作用下的固结将严重低估吹填土的固结程度。