栏杆对钢引桥受力的影响
2020-08-04唐艺航黄晔卉
唐艺航,黄晔卉
(中交上海航道勘察设计研究院有限公司,上海 200120)
关键字:钢引桥;有限元
引 言
在港口工程中,关于钢引桥的使用已经相当广泛[1]。栏杆作为其附属结构,设置在行车道板上,用以封闭沿线两侧,防止车辆以及行人越出桥外。
在钢引桥结构设计中,一般不考虑栏杆对该结构受力的影响,只是将栏杆当成外部荷载与其它荷载一同施加在结构上。但大量研究表明,栏杆对桥梁结构受力有一定影响[2-4]。若不考虑栏杆的作用,其计算结果不完全符合钢引桥结构的实际受力情况,计算结果过于保守。关于栏杆对钢引桥结构受力的影响,目前还没有相关研究成果。
基于以上情况,本文以某工程钢引桥为研究对象,利用通用有限元软件 ABAQUS分别建立考虑栏杆作用和未考虑栏杆作用的实体有限元模型。在相同设计荷载工况作用下,对比分析栏杆对钢引桥结构的刚度,应力以及模态的影响,并为以后该类结构的设计及结构检测提供依据。
1 工程概况
1.1 结构型式
本文的研究对象为某工程钢引桥。该钢引桥结构由纵横梁格、桥面板及锚栓拉杆组成。
该结构跨度为12.8 m,其中计算跨度为12.5 m,横向宽度为1.5 m。主梁采用拼接工字钢,主梁中心距为1.25 m,其受力为简支受力体系。该结构的平、立面,跨中断面以及支座处断面见图1~图3。各结构构件采用的截面形式如表1所示。
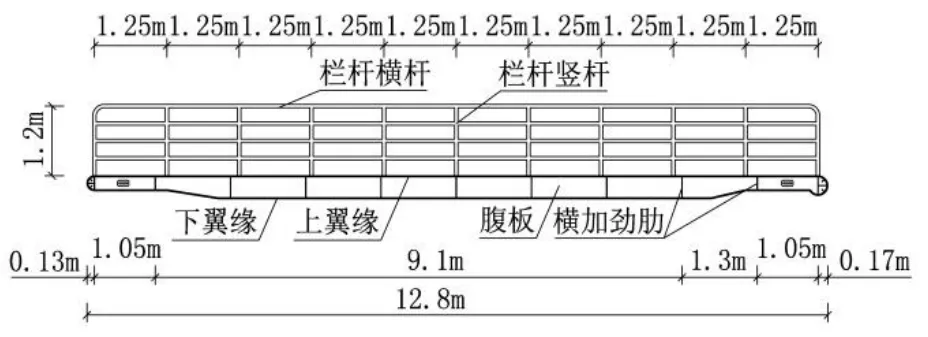
图1 钢引桥立面示意
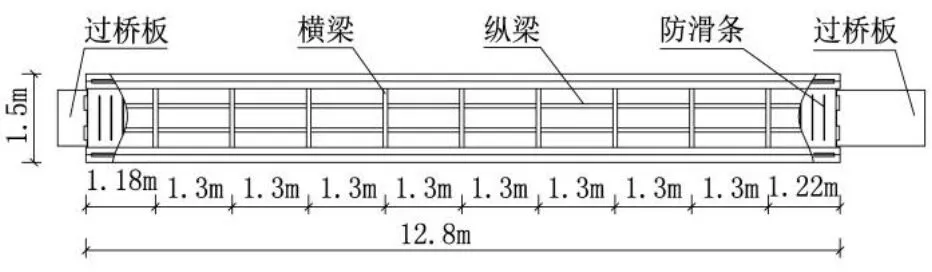
图2 钢引桥平面示意
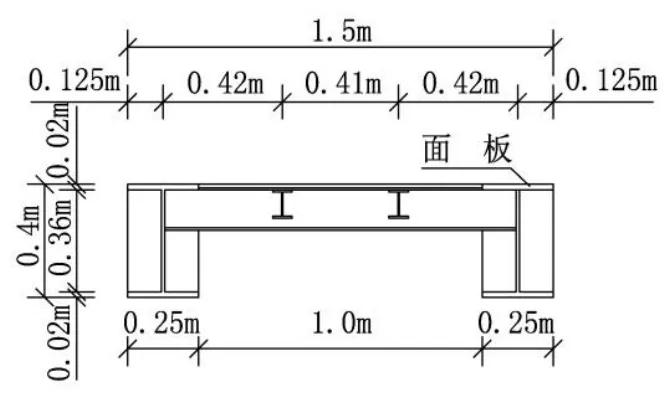
图3 钢引桥典型断面
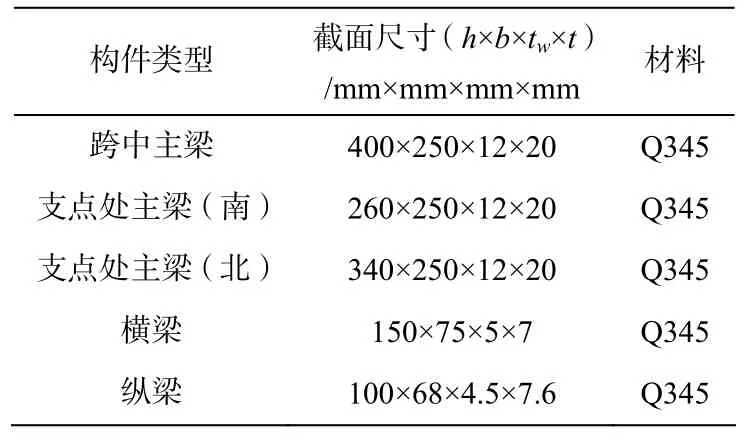
表1 钢引桥构件截面形式
1.2 栏杆构造
本工程钢引桥采用钢管防护栏杆,栏杆横竖向规则布置,钢管材料为 Q345,直径为 60 mm,厚度为3.5 mm,竖向钢管水平间距为1.25 m,横向钢管竖向间距 0.3 m。栏杆节点采用角焊缝连接,坡脚尺寸为6 mm。栏杆与钢引桥采用角焊缝连接,坡脚尺寸为8 mm。
1.3 荷载条件
钢引桥主要承受的荷载有:本身自重以及人群荷载,其中人群荷载取3 kPa。
2 有限元建模过程
2.1 有限元介绍
有限元法是一种高效能、常用的数值计算方法,现在已经广泛运用于结构的数值模拟。有限元模型按照其单元类型可分梁单元模型,实体单元模型,板壳单元模型等。
实体单元可以通过其任意表面与其他单元连接,故该模型几乎可以模拟任何结构形式。通常认为,当单元划分足够精细,并且单元无明显畸变时,其计算结果较贴合实际情况,即在一定程度上其计算结果可认为是精确解。
2.2 有限元建模
根据上述已有参数,主梁、横梁及纵梁采用Q345钢,材料的弹性模量取2.06×105MPa,泊松比为0.3,容重为76.93 kN/m3。利用通用有限元软件ABAQUS分别建立考虑栏杆作用和未考虑栏杆作用的实体单元模型。结构离散模型见图4。
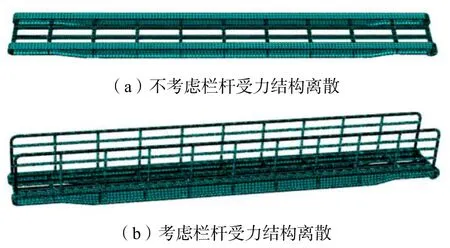
图4 钢引桥实体单元有限元模型
在单元选择方面,钢引桥结构主体采用ABAQUS中提供的C3D8R单元,即八结点线性六面体单元,该单元可以以较小的费用得到较好的结果。栏杆结构由于节点处结构不规则,故采用ABAQUS中提供的C3D10单元,即十结点二次四面体单元,该单元能有效模拟节点处受力情况。本文采用ABAQUS中提供的绑定约束方法来模拟栏杆节点及栏杆与钢引桥连接处焊缝连接。
3 计算结果及分析
3.1 挠度结果对比
1)荷载工况
本文挠度分析时荷载组合采用标准组合,即1.0自重+1.0人群。
2)对比点布置
在钢引桥结构设计时,主要通过保证主梁下缘竖向挠度值小于设计要求以此来保证结构刚度满足规范要求,故本文只分析栏杆对主梁下缘挠度的影响。
为了更全面的了解栏杆对钢引桥主梁挠度的影响,本文在主梁下翼缘上设置了11个对比点,对比点的具体位置和编号如图5所示。
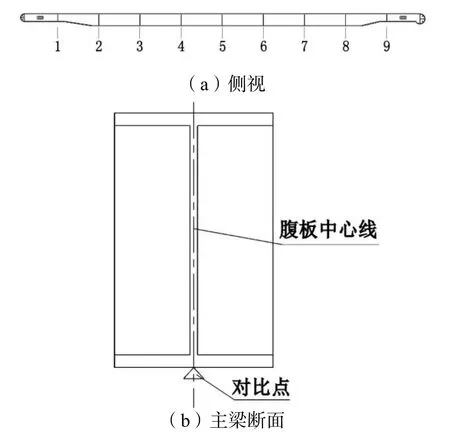
图5 主梁对比点布置
将荷载工况下挠度值计算结果进行对比,结果见图6,具体数据见表2。由表2可看出,考虑栏杆参与受力后各对比点挠度值可减小30 %以上。由此可知,考虑栏杆参与受力后对结构的竖向刚度有较大的影响,其作用不可忽略。
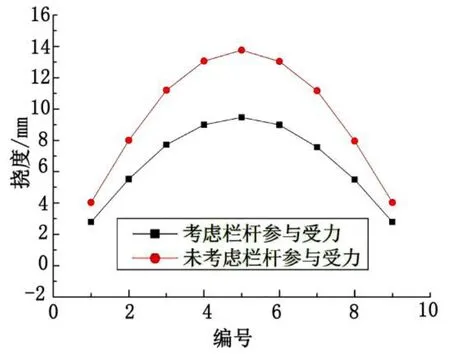
图6 设计工况下挠度对比
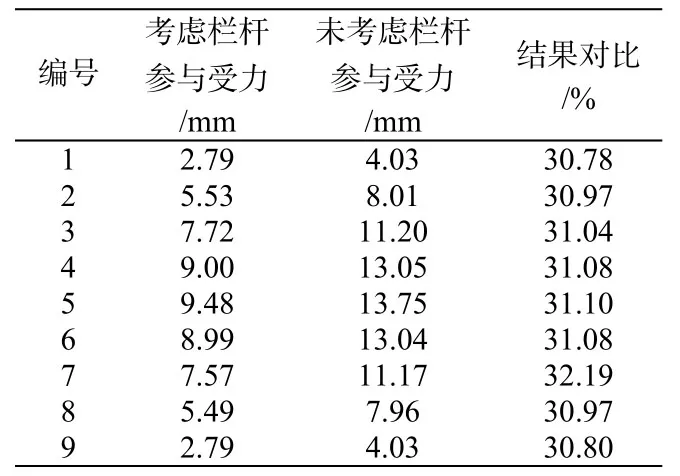
表2 挠度对比结果
3.2 应力结果对比
本文钢引桥结构主要受力构件为主梁以及横梁,纵梁只是起到增强横梁间的连接,提高钢引桥的整体性的作用。故本文主要分析栏杆引起的主梁和横梁的内力变化情况。
在进行应力结果对比分析时,荷载工况采用基本组合,即1.2自重+1.4人群。本文中的应力值均为Mises应力。
1)主梁应力分析
为了全面了解栏杆对结构主梁应力的影响,本文分别对比11个对比点处上下翼缘所受的应力。对比点的具体位置如图7所示。
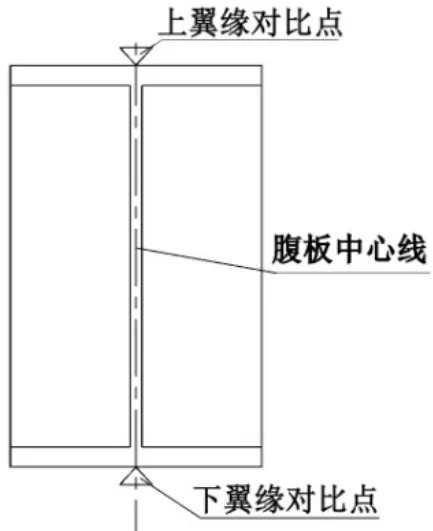
图7 对比点位置
将设计荷载工况下应力计算结果进行对比,结果见图8,具体数据见表3~表4。
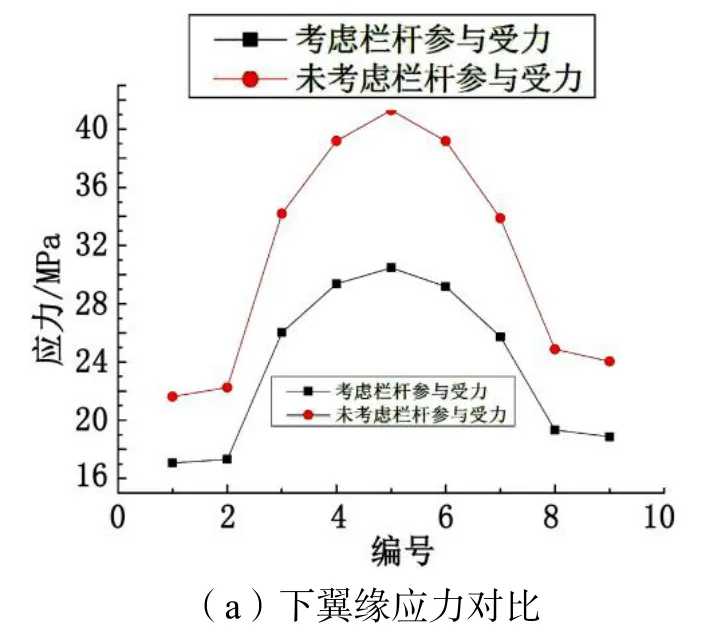
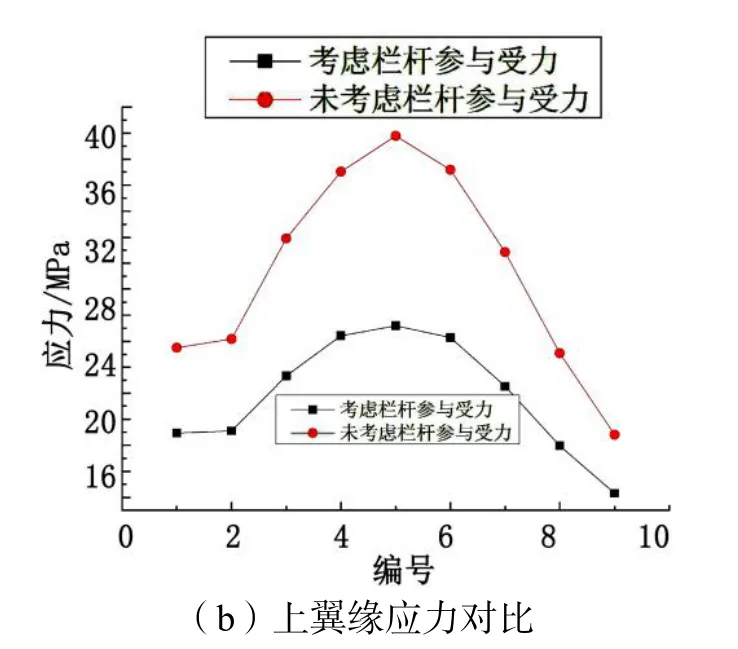
图8 设计工况下应力对比
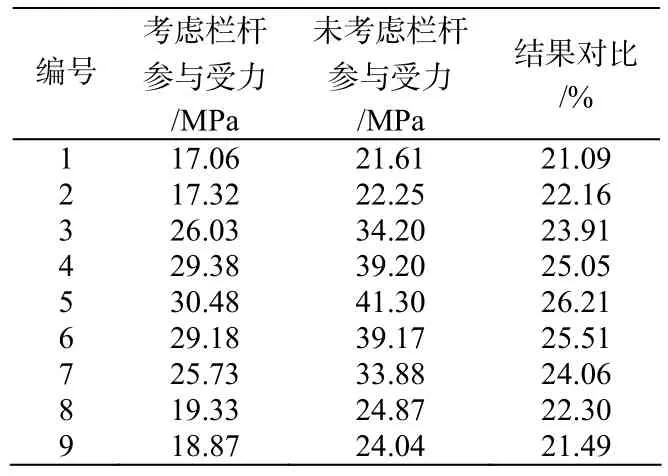
表3 下翼缘应力对比
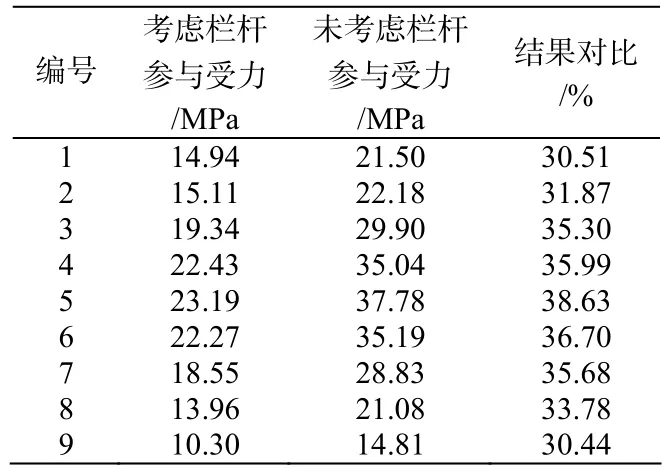
表4 上翼缘应力对比
从表3可知,考虑栏杆作用后,各位置处主梁的下翼缘应力值都有所减小。其中5号点位置即跨中位置处应力值降幅最大,为26.21 %。1号点位置应力值即支座位置处降幅最小,为 21.49 %。从表中还可以看出,越接近跨中位置,栏杆对应力值影响越大。
从表4可知,同下翼缘受力情况类似,考虑栏杆作用后,各位置处应力值都有所减小。其中5号点位置即跨中位置处应力值降幅最大,为38.63 %。1号点位置即支座位置处降幅最小应力值降幅最小,为30.51 %。且越接近跨中位置,应力值减小程度越大。对比分析表3、表4可以考虑栏杆作用后,与下翼缘相比,上翼缘应力值减小程度更显著。
2)横梁应力分析
由于横梁个数较多,且受力情况类似,故本文着重对比分析设计荷载工况下受力最大的横梁(受力最大指应力最大)。通过计算发现,支座处的横梁为受力最大的横梁。故对比分析该横梁的应力。
为了全面了解栏杆对结构横梁应力的影响,本文在横梁设置了5个对比点,分别对比该点些上下翼缘所受的应力。对比点的具体位置和编号如图9所示。
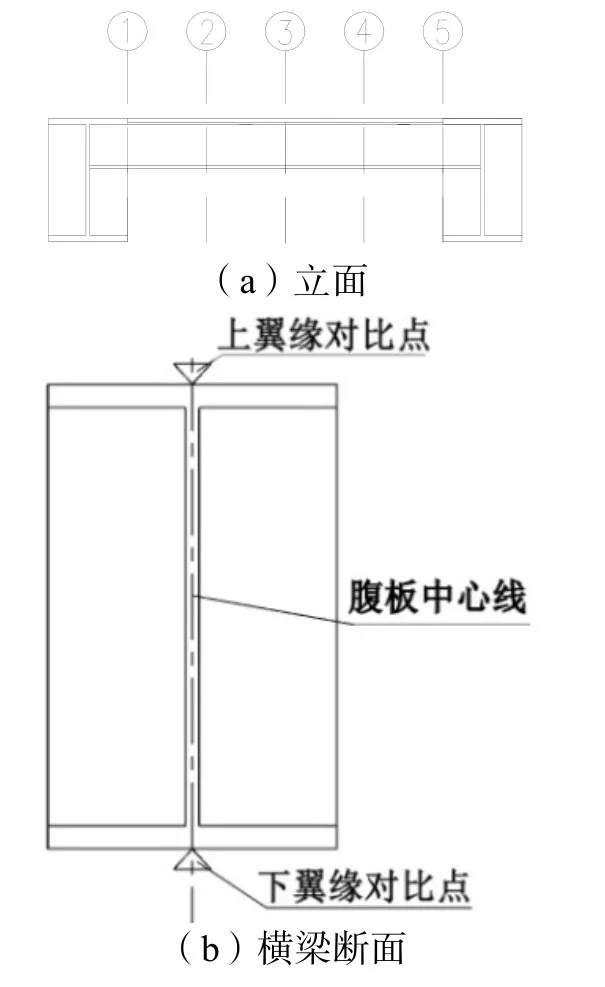
图9 横梁对比点布置
将设计荷载工况下应力计算结果进行对比,结果见图10,具体数据见表5~表6。
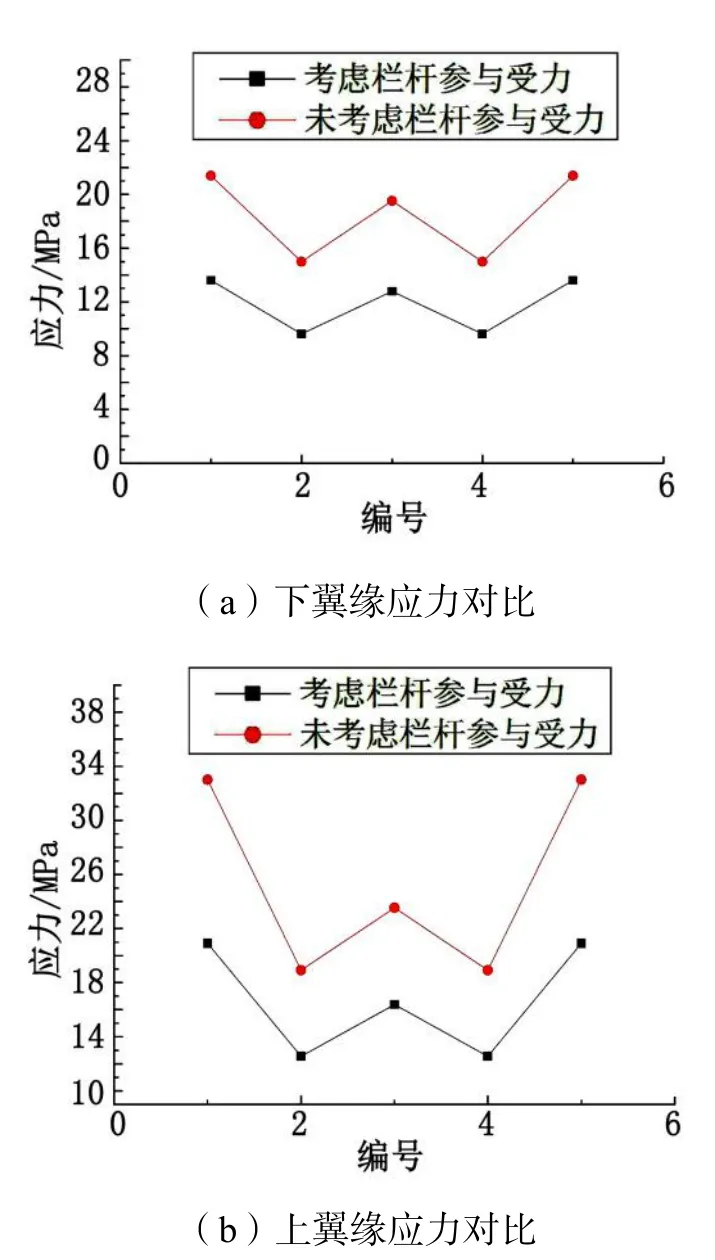
图10 设计工况下横梁应力对比
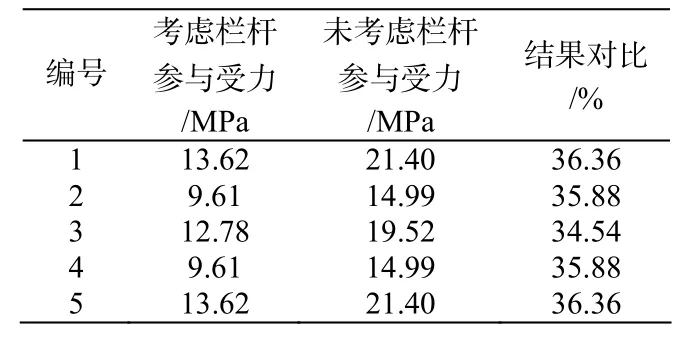
表5 下翼缘应力对比
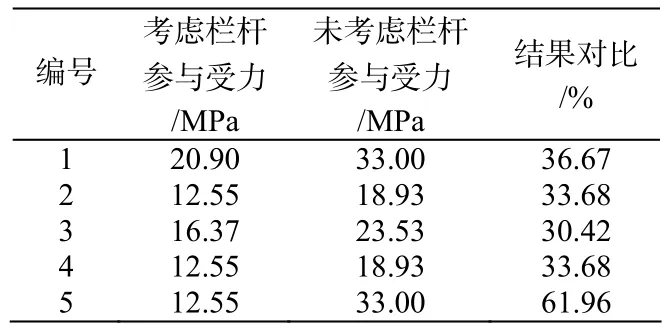
表6 上翼缘应力对比
从表5可知,考虑栏杆作用后,各位置处横梁的下翼缘应力值都有所减小。其中1和5号点位置即节点位置处应力值降幅最大,为36.36 %。3号点位置即跨中位置处应力值降幅最小,为34.54 %。同时可以看出,越接近节点位置,栏杆对应力值影响越大。
从表6可知,考虑栏杆作用后,各位置处应力值都有所减小。其中1和5号点即节点位置处应力值降幅最大,为36.67 %。3号点即跨中位置处应力值降幅最小,为30.42 %。与下翼缘情况类似,越接近节点位置,栏杆对应力值影响越大。
3.3 特征值分析
结构自振周期只与自身质量以及结构刚度有关。当质量一定时,自振周期可以反映结构刚度大小。故可采用计算自振周期的方式研究栏杆对结构横向刚度及抗扭刚度的影响。
本文通过通用有限元程序软件 ABAQUS计算得到钢引桥前4阶固有振型以及其结构的自振周期,周期结果对比见表7。
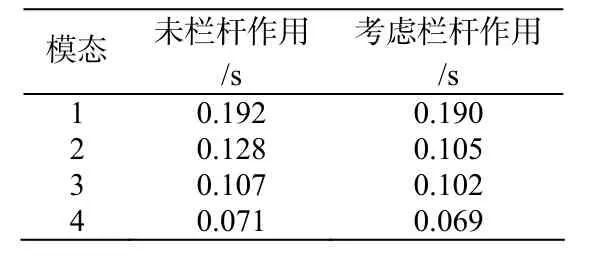
表7 特征值周期结果对比
从表7可知,考虑栏杆作用后对结构振型影响不大。在自振周期方面,除二阶模态所对应的周期相差较大,误差达到15 %以外,其余周期均在4 %以内。说明了栏杆对结构竖向刚度影响较大,但对结构的横向刚度及抗扭刚度影响较小。
4 结 语
通过通用有限元软件 ABAQUS分别建立考虑栏杆作用和未考虑栏杆作用的实体有限元模型,在相同设计荷载工况作用下,对结构进行受力分析,得到以下结论:
1)考虑栏杆作用后,在相同荷载作用下结构主梁挠度有明显减小,说明栏杆对结构的竖向刚度有较大的影响,其作用不可忽略。
2)考虑栏杆作用后,主梁的上下翼缘应力值均有所减小,减小幅度在30 %以上,且越接近跨中位置,应力值减小程度越大。较下翼缘相比,上翼缘应力值减小程度更显著。
3)考虑栏杆作用后,横梁的上下翼缘应力值均有所减小,减小幅度达到30 %以上,且越接近节点位置,栏杆对应力值影响越大。
4)栏杆对结构振型影响不大。在自振周期方面,除了二阶模态所对应的周期相差较大,误差达到15 %,其余周期均在4 %以内。说明栏杆主要影响结构的竖向刚度,但对结构的横向刚度及抗扭刚度影响较小。
5)在结构设计不考虑栏杆的作用,其计算结果较保守,偏于安全。但在结构检测时若不考虑栏杆的影响,其结果偏于不安全,故在检测时,应结合栏杆实际结构形式及布置情况,考虑栏杆对结构受力的影响。
