基于粒子群优化的神经网络算法的英语翻译

孙 荧, 王 荆

(1.西北工业大学外国语学院, 西安 7100722;2.国网陕西省电力公司电力科学研究院， 西安 710100)

中国具有世界最庞大的英语学习群体。然而，由于师资力量的不均以及地区教育的差异，中国的英语学习者所接受到的英语教育水平存在着较大的差异。基于人工智能的教育教学模式是解决这一问题的良好途径[1-2]。人工智能系统通过学习采集到的大量样本数据，可以达到一定的智能程度，例如在图像识别、无人驾驶、语音识别等领域，人工智能已取得出色的成绩，在某些方面，尤其是英语翻译等，完全可以取代人类的工作[3-4]。近年来，基于人工智能的英语翻译模式一直是业界的焦点。Hameed等[5]学者研究智能系统通过采集并学习大量的学生学习状态、性格及年龄等相关信息，建立一个学习能力的分析模型，并利用这种模型分析人在英语翻译中的特点，为英语翻译算法提供帮助。随着信息技术的发展，这种英语翻译系统可以在一定程度上消除英语教育资源的不均所带来的教育差异[6]。所以对英语翻译算法的研究是十分必要的。在英语实际应用场景中，Behnamian[7]基于人工智能建立听力资源的语料库，可以自动分配听力资源，同时也可以实现情境交互，从而增强了翻译的准确性。基于云平台的人工智能技术是另外一个研究热点之一，Moradi等[8]研究者利用云平台的大数据处理计算能力，将人工智能引入翻译，云平台系统可以追踪人工翻译的译文，及时准确地了解每个语言场景的翻译特点从而量化的输出翻译结果[9-13]。基于此，探索人工智能能否在英语翻译活动中作用，用粒子群优化算法加速神经网络的训练，使其可以更快地收敛。用真实教学样本数据进行测试，从而验证方法的可行性。

1 粒子群优化算法的分析研究

1.1 粒子群优化算法的数学模型

假定粒子群中i粒子的粒子坐标为Xi=(xi1,xi2,…,xin),最佳位置是记为p1,所有粒子的最佳记录位置为p2,粒子的移动速度为Vi=(vi1,vi2,…,vid)。在粒子的搜索过程中，每一次迭代过程，粒子在空间中的轨迹如式(1)和式(2)所示。

(1)

(2)

式中：c1和c2分别为加速度常数，其目的是使粒子更快地向最佳位置和所有粒子的最佳位置移动；rand()为[0,1]的随机数；粒子移动速度的最大值为Vmax。当粒子的速度达到最大值Vmax时，速度不会增加，但会保持速度不变。设定粒子速度最大值的目的就是为了在整个搜索过程中提高搜索精度。当粒子速度过高时，会导致粒子错过当前解空间的最优值；当粒子速度过小时，粒子会陷入局部最优解。因此，这种设置是必要的。

从式(1)可以看出,粒子的速度主要由三部分组成，第一部分是粒子的初始速度运动,描述粒子的运动状态,在没有任何干扰,粒子的速度将保持不变。第二部分是粒子的认知能力，这个过程可以模拟鸟类的认知行为。第三部分是信息的共享，在优化过程中粒子之间会有相互作用，可以使整个粒子群共同进化，体现了粒子的社会学特征。

1.2 粒子群优化算法的流程

大多数优化算法都是基于梯度信息进行优化的，但粒子群优化不需要梯度信息，粒子群优化是一种利用概率模糊搜索的方法。在实际优化过程中，虽然需要大量的评价函数来确定粒子的适应度，但与传统的进化算法相比仍有许多明显的优势。

在粒子群优化过程中，问题的整体解的质量不会受到个体的影响，因此具有较高的鲁棒性。此外，整个粒子群中的个体之间的信息交换并不是直接进行的，因此可以保证整个系统具有良好的可扩展性。在求解粒子群优化算法的过程中，可以采用分布式处理模式，通过协调多处理器进行并行计算，提高了整体求解的效率。粒子群优化算法不需要问题的特定连续性，与传统的智能算法相比具有更高的可扩展性。粒子群优化算法的一般流程如图1所示。

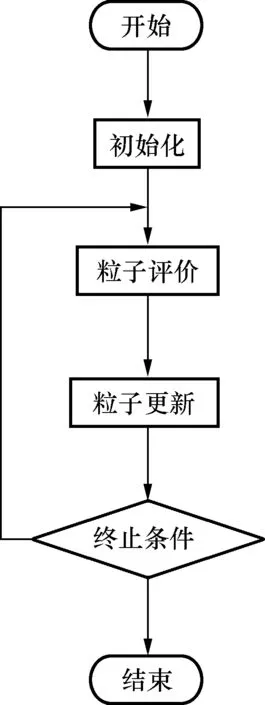
图1 粒子群优化的步骤Fig.1 General steps of particle swarm optimization

2 基于粒子群优化神经网络的英语翻译的应用分析

2.1 人工神经网络模型

人工神经网络通常由多个神经元和多个节点组成，多层前馈神经网络模型是应用最广泛的神经网络模型，主要包括输入层、输出层和隐藏层。输入层主要是从外部获取所需信息，然后将获取的信息输入到神经网络中，等待后续处理；隐藏层是指加工的过程；输出层是将处理的结果输出到所需的位置。

2.2 英语翻译应用模型

在英语翻译的教学过程中，如何获得客观的数据并利用这些数据进行正确的分析是非常重要的。因此，提出一个应用模型来分析学生在英语翻译教学过程中的学习能力,即学习能力分析模型，如图2所示。

图2 学生学习能力分析模型Fig.2 Analysis model of students learning ability

学习能力分析模型的目的是分析学生在英语翻译学习过程中的一些与学习相关的特点，通过分析得出学生学习状态的相关信息，并且利用分析的结果，为学生制定有针对性的教学任务，从而促进英语翻译教学的发展。在数据采集阶段，主要通过问卷调查的方式进行初步的数据采集。在数据提取阶段，需要对原始数据进行预处理，消除无用数据对整个分析过程的干扰。由于原始数据的部分缺失和遗漏，不完整，需要按照一定的标准填写填充过程，然后将处理后的数据输入神经网络进行分析。

再者，需要确定神经网络模型的拓扑结构、输入层的节点数、输出层的节点数和隐藏层的节点数。隐藏层节点的计算公式如式(3)所示。

(3)

式(3)中：J为隐藏层节点数；M为输出层节点数；N为输入层节点数。根据式(3)可以得到网络训练次数与隐藏层节点数之间的关系。为了简化两者之间的关系，绘制网络训练次数和隐藏层节点数。如图3所示，当神经网络隐藏层的节点数为4时，整个网络模型的训练次数最短。

图3 隐藏层节点数和训练次数的关系Fig.3 The relation of the training time and hidden layer node number

2.3 基于粒子群优化神经网络的应用求解

将粒子群算法的优化原理引入神经网络，增强了算法的全局寻优能力;该复合算法利用粒子的移动和更新来寻找初始阶段神经网络的最优解，算法的执行流程如下。

Step 1对特征数据的预处理。

在人工神经网络的学习过程中，为了消除大值数据对基于模型的预测或诊断的影响，对数据进行归一化处理。数据的变化被限制在一定范围内，通常是在(0,1)。因为Sigmoid函数用作神经网络的输出层的转换函数，Sigmoid传递函数具有特殊的特征，当x接近正值时或负无穷大，输出值将接近0或1，因此输出变量范围为(0,1)。没有规范化数据，小值神经元对网络的影响可能远远小于大值神经元，从而影响训练结果，归一化公式如式(4)所示：

(4)

对输出值进行反归一化处理,反归一化公式如式(5)所示：

(5)

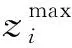
Step 2设置神经网络相关参数。

采用BP(back propagation)神经网络对代价模块进行估计，其中BP神经网络有几个重要参数，包括隐藏节点数、隐藏层数、激活函数、学习率、动量系数。

(1)隐藏节点数：隐藏节点越多，收敛速度越慢，但误差可能越小，尤其是“训练样本”误差。但是，当数量增加到一定程度时，再增加数量也不能减少错误，执行时间可能会突然延长。采用式(3)计算隐藏层节点数。

(2)隐藏层数：隐藏层数对于网络的收敛速度有着重要的影响，通常1～2层较为理想且可以解决大多数应用问题。采用一层进行训练。

(3)激活函数：Sigmoid函数用来作为激活函数,其计算公式如式(6)所示:

(6)

式(6)中：t为Sigmoid函数的自变量。

(4)学习率及动量系数：学习率对网络的收敛速度有显著影响,通常取η=0.1～1.0,一般情况下，学习算法会附加一个动量系数，即加入一定比例的之前的权值变化，以减弱收敛中的振荡，加速收敛。设置η+μ=1.0。

Step 3随机生成粒子群的初始速度和位置

设置Xi=(xi1,xi2,…,xin)为粒子i初始位置,设置Vi=(v1,vi2,…,vid)为粒子i初始速度，Pg=min{P0,P1,…,Ps}为所有粒子的最佳位置记录,即局部最优位置,粒子群在n维空间中的速度和位置向量在(0,1)随机生成。

Step 4计算神经网络前向的输出向量。

隐藏层输出向量H如式(7)、式(8)所示。

(7)

(8)

式中：th表示第h层的输入加权和；aih为第i层与第h层之间的联接参数；xi为第i层的激活值；θh表示第h层的偏置量。

计算输出层的向量Y如式(9)、式(10)所示：

(9)

(10)

式中：tj为第j层的输入加权和；Yj为第j层的输出量。

Step 5计算反向差δ:

δj=Yj(1-Yj)(Tj-Yj)

(11)

(12)

Step 6计算权重矩阵Δw及偏置向量Δθ变化量：

Δwhj=-ηδjHh

(13)

Δθj=-ηδj

(14)

更新权重矩阵与偏置向量，得：

(15)

(16)

Step 7计算每个粒子的适应度。

根据问题特定的目标函数估计每个粒子的适应度，将适应度函数值与记忆中的最佳函数值进行比较，然后粒子根据记忆中的最佳值修改下一阶段的搜索速度。误差平方和(sum of squared error，SSE)如式(17)所示：

(17)

式(17)中：Ti为算法拟合出的数据；Ei为原始数据。

Step 8记录粒子位置并更新其位置速度向量。

将粒子最佳值与全局最佳值进行比较，如果粒子最佳值优于全局最佳值，则修改内存中的全局最佳值,同时每个粒子修正位置速度,为下一次全局搜索准备。

(18)

(19)

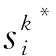
Step 9应用粒子群优化的神经网络算法模型对英语翻译教学效果进行验证。

当粒子群达到全局最优状态时,网络训练完成,得到训练集的平均误差数据,用样本集数据进行测试得到误差数据.

3 案例应用和结果分析

应用粒子群优化的神经网络算法模型对英语翻译教学效果进行了验证。首先，完成对学生英语翻译学习特征的样本采集，然后分两个步骤进行，第一步利用粒子群优化算法对神经网络进行训练；第二步对模型的有效性进行评估和测试。

数据集作为神经网络算法实现中关键的一环，对模型输出结果的可信起着决定性的作用。从阿里巴巴公司的Tianchi Data Sets中获取2 000条学生英语翻译数据，在保证样本多样性的前提下剔除数据集中没有对应翻译结果、显示模糊、无法提取特征点的数据；同时，为了在不影响模型有效性的前提下增加数据量，提高模型的泛化能力，对数据进行了增加噪声等数据增广操作，使数据集中包含有4 500条可测试的数据。通过上述过程获得的数据集，能够最大程度的保证英语翻译特征样本采集结果的准确性和多样性。

当使用粒子群优化算法对神经网络进行训练时，不仅需要对已有的数据进行处理，还需要设置一些参数。将早熟因子设置为0.01，其他参数以随机形式产生。根据粒子群算法选择粒子群规模的惯例，设置3个不同的粒子数，即5、10、20，并分析3种不同粒子数的运行效率。当迭代次数分别达到243、437、295时，算法输出的结果与训练样本、测试样本之间的误差以足够小，并保持一段时间没有更优的解出现。因此此时结果即为最优解，随即停止迭代，记录相关数据如表1所示。

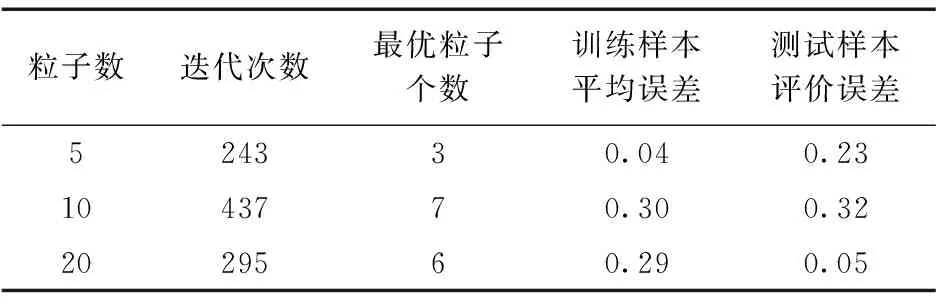
表1 粒子群优化的神经网络模型的案例结果Table 1 Experimental results of the particle swarm optimization algorithm to train the neural network

结合英语翻译的实践，由表1可以看出,采用粒子群优化算法对神经网络进行训练，可以得到不同粒子数种群的最优解，并且误差值较小。基于所提出的学习分析模型，可以用样本训练好的粒子群优化的神经网络模型对学生的英语翻译能力进行正确程度的分析，帮助教师估计学生的翻译能力水平，为下一步的教学提供参考。

4 结论

通过研究粒子群优化算法的数学模型和算法流程，以及人工神经网络模型的基本原理；并基于粒子群优化的神经网络模型，提出了学习能力分析模型，确定了该模型的神经网络的拓扑结构和隐藏层的节点数；基于英语翻译教学的样本数据，建立了研究模型。通过对实验结果的分析，发现本文方法可以帮助教师估计学生的翻译能力能力水平，为学生进一步提高英语翻译水平提供参考。所提出的应用人工智能算法帮助英语教学的研究方法，随着计算机技术的进一步发展，可以在广泛推广至英语教学的众多方面。