基于TSK型递归模糊神经网络的加工中心双直线电机交叉耦合同步控制
2020-08-04方昱璋张晓梅张海文
方昱璋, 张晓梅, 张海文
(国网甘肃省电力公司经济技术研究院, 兰州 730050)
科技的飞速进步使伺服系统对于高速度高精度镗洗加工技术的要求越来越高,通常需要对大型零件和复杂的几何型面进行高精密加工[1-2]。移动式龙门镗铣床克服了传统固定式镗铣床受工作地点约束、体积质量大的缺点,在多电机协同系统受到更大的关注。而移动式龙门镗铣床加工机构需要两台完全相同且相互平行的永磁直线同步电动机(permanent magnet linear synchronous motor,PMLSM)构成,尽管安装在X轴的两台电机具有相同的结构与参数,但在PMLSM加工制造过程中难免会出现结构上的细微差异,以及在两台PMLSM运行过程中受参数变化、外部扰动等不确定性因素的影响,都会造成系统控制性能的降低[3]。在机床实际运行过程中,加在工作台上的负载质量变化,也会导致两台PMLSM之间存在受力不平衡的现象,致使两个PMLSM子系统输出不同步,从而产生同步误差[4]。
为提高双直线电机伺服系统的同步跟踪精度,中外学者进行了深入研究,主要研究方向为提高单轴PMLSM跟踪精度和双电机同步精度两方面[5]。文献[6]中将一种概率模糊神经网络控制器应用于PMLSM伺服系统,虽然具有强大的在线学习能力,但隐含层节点数目太多,导致神经网络控制器在设计时较为复杂。文献[7]针对加工中心双直线电机系统设计了自适应模糊滑模控制器,保证了系统的跟踪性,但其单轴PMLSM子系统仅采用PI控制器,性能有待提高。文献[8]将积分滑模控制应用于双永磁同步电机中,解决了电机受负载扰动而转速不同步的问题,但其采用的积分滑模控制仍存在抖振现象。文献[9]从龙门平台的结构上出发,在建立了精准的龙门平台数学模型的基础上,提出了一种直接考虑附加旋转动力学的自适应鲁棒同步控制方案,该方法带有在线参数估计器,不仅能使两台并联电机的运动同步,而且还能调节电机的转速。
为提高龙门镗铣床加工中双直线电机伺服系统的同步跟踪精度,采用一种TSK型递归模糊神经网络(TSK-type recurrent fuzzy neural network,TSKRFNN)与交叉耦合控制(cross-coupled control,CCC)相结合的控制方法。该方法充分考虑了双直线电机伺服系统的特点,分别从单轴和双轴两方面提高系统性能。利用TSKRFNN提高系统鲁棒性;同时利用CCC消除机械耦合引起的同步误差。实验结果表明,该方法有效地提高了双直线电机的同步运行精度,适于应用在同步控制中。
1 PMLSM数学模型
由于两台PMLSM完全相同,因此,仅以一台PMLSM为例建立数学模型。PMLSM的简化电磁推力方程为
Fei=Kfiiqi
(1)
Kfi=3πnpiλPMi/2τi
(2)
式中:Fei为PMLSM的电磁推力;Kfi为电磁推力系数;iqi为q轴电流;i=1,2,分别表示PMLSM1和PMLSM2。
PMLSM的动态方程为
(3)
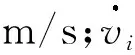
2 基于TSKRFNN的双直线电机交叉耦合控制系统设计
针对双直线电机系统易受不确定性因素的影响,且系统运行过程中由于负载力的变化以及环境的变化等会存在参数不匹配,不平衡力等耦合问题,采用基于TSKRFNN的双直线电机CCC方法以解决以上问题。基于TSKRFNN的双直线电机CCC方法系统总框图如图1所示。从图1可以看出,两台PMLSM采用并行控制方式,对两台电机输入相同的位置给定信号,同时每个轴均采用相同的传感器装置、伺服驱动器等组成控制回路。
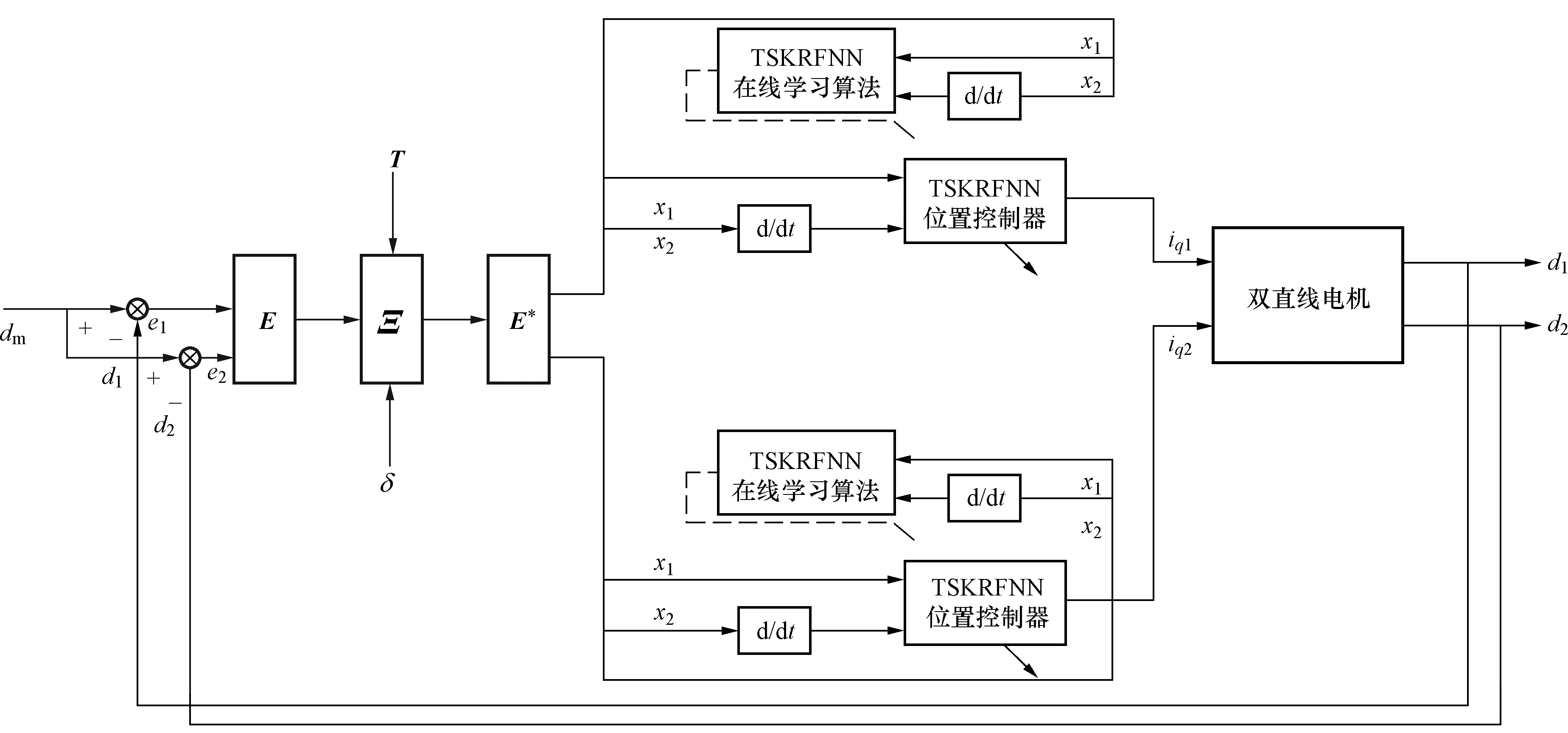
图1 基于TSKRFNN的双直线电机CCC方法系统总框图Fig.1 Block diagram of dual linear motor based on TSKRFNN and CCC
2.1 CCC设计
采用CCC方法消除双轴之间存在的同步误差,CCC方法能够将两个子系统产生的单轴位置跟踪误差按照一定比例分配到两轴中,从而达到平衡。首先,定义单轴PMLSM位置跟踪误差为
ei=dm-di
(4)
式(4)中:ei为两台电机的位置跟踪误差;dm为直线电机给定位置;di为实际位置。
为减小同步误差,需找到同步误差与单轴位置跟踪误差之间的关系。定义两轴间同步误差为
(5)
式(5)中:ε1、ε2为双直线电机的同步误差,即两台PMLSM的跟踪误差的差值。为方便分析控制器的设计,将式(5)表示为

(6)
为同时减小两台PMLSM的跟踪误差和同步误差,得出两者间关系为

(7)
式(7)中:E*为耦合误差,且E*=[x1x2]T;δ为耦合参数,且δ>0。将式(6)代入式(7)得:
E*=(I+δT)E
(8)
式(8)中:I为单位阵;(I+δT)为正定矩阵。
2.2 TSKRFNN设计
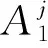
图2为TSKRFNN的结构框图。每层网络具体介绍如下。
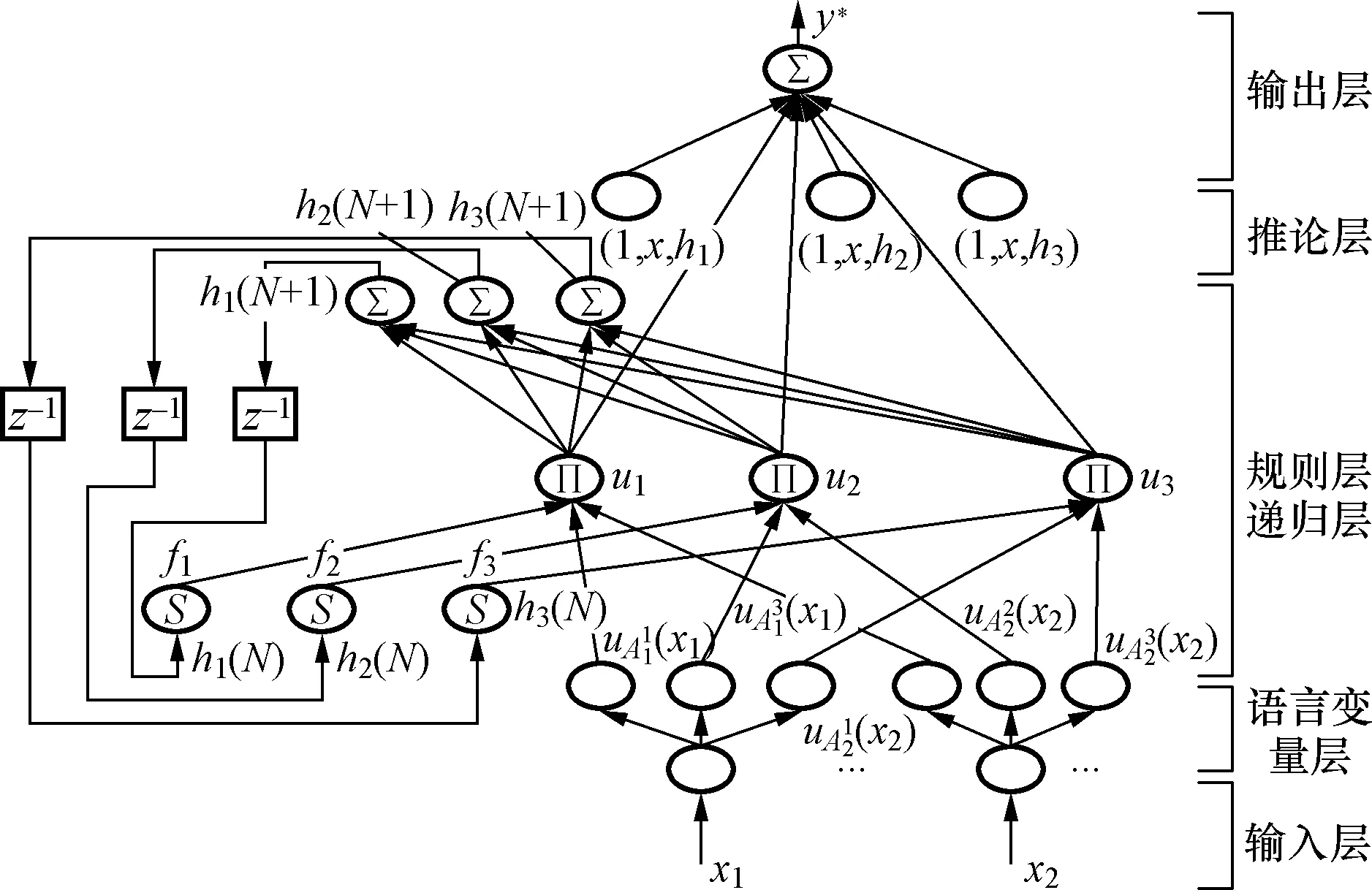
图2 TSKRFNN结构框图Fig.2 Structure diagram of TSKRFNN
输入层:TSKRFNN为双输入神经网络。耦合误差x1和耦合误差的微分x2作为网络的输入。
语言变量层:此层中隶属函数采用高斯函数为
(9)
式(9)中:mij和σij分别为高斯函数的平均值和标准差。
规则层:将内部变量hk以S型隶属函数的形式可以描述为
(10)
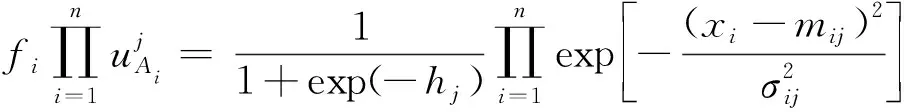
(11)
推理层:本层中节点采用线性加和的方式进行传播。节点j描述为
(12)
式(12)中:Tj=(1,x,hj);aij为可以调整的参数值,i=0,1,…,n+1。
输出层:此层输出信号y*表示为
(13)
定义能量函数V表示为
(14)
TSKRFNN可以对双直线电机系统中存在的不确定性因素的值进行估计,同时根据估计值对网络中参数进行在线调整。TSKRFNN可以利用一定的规则进行参数优化,具体描述如下。
输出层:输出层误差δ5描述为
(15)
(16)

(17)
(18)
aij、θjk、mij和σij的更新律分别表示为
(19)

(20)
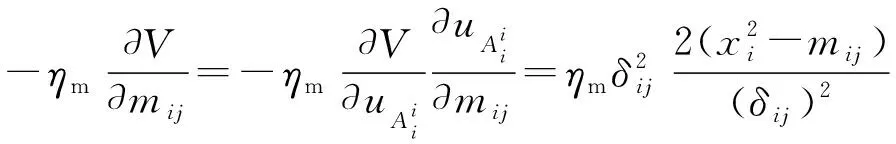
(21)

(22)
式中:Δaij、Δθjk、Δmij和Δσij为aij、θjk、mij和σij的更新律;ηa为连接权重;ηθ为递归权重;ηm为平均数的学习速率;ησ为标准差的学习速率。
隶属度函数和权重的平均数和标准差优化为
aij(N+1)=aij(N)+Δaij
(23)
θjk(N+1)=θjk(N)+Δθjk
(24)
mij(N+1)=mij(N)+Δmij
(25)
σij(N+1)=σij(N)+Δσij
(26)
式中:N为迭代次数。
3 实验结果及分析
利用数字信号处理器(digital signal processor,DSP)DSP作为控制核心,对系统进行实验。实验装置如图3所示。实验中所选PMLSM参数:M=5.8 kg,B=2 N·s/m,Kf=10.97 N/A。TSKRFNN中选取网络参数:ηa=1.25,ηθ=0.17、ηm=0.34和ησ=0.05。

图3 实验装置Fig.3 Experimental setup
为验证所提出的TSKRFNN双直线电机CCC方法的有效性,在参数变化(实际动子质量Ma=2M,实际黏滞摩擦系数Ba=1.5B)的情况下对双直线电机伺服系统给定如图4所示的梯形位置信号。基于TSKRFNN和TSKRFNN+CCC的位置跟踪误差曲线及同步误差曲线分别如图5、图6所示。对比两条曲线可以看出,在仅有TSKRFNN控制时,两台电机的位置跟踪误差均较大,从而导致同步误差在-1.5~1.5 μm之间波动。而在TSKRFNN+CCC控制下, 两台电机的位置跟踪误差和同步误差均得到了改善,同步误差约为-0.7~0.7 μm。因此,针对含有不确定性和耦合问题的双直线电机系统,所提方法能够有效减小跟踪误差和同步误差,提高同步控制精度。

图4 梯形位置给定信号Fig.4 Trapezoidal position given signal
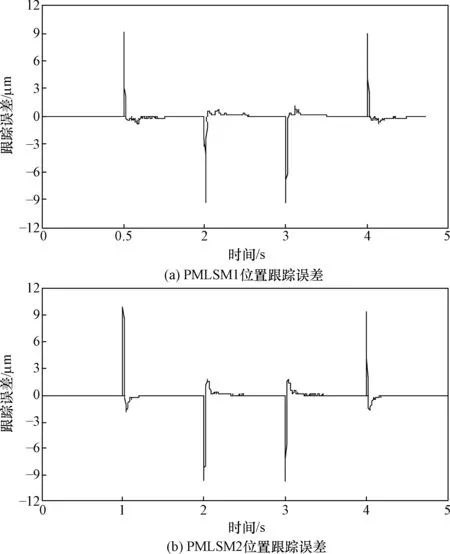
图5 基于TSKRFNN的双直线电机伺服系统位置跟踪误差及同步误差曲线Fig.5 Position tracking error and synchronization error curves of dual linear motor servo system based on TSKRFNN
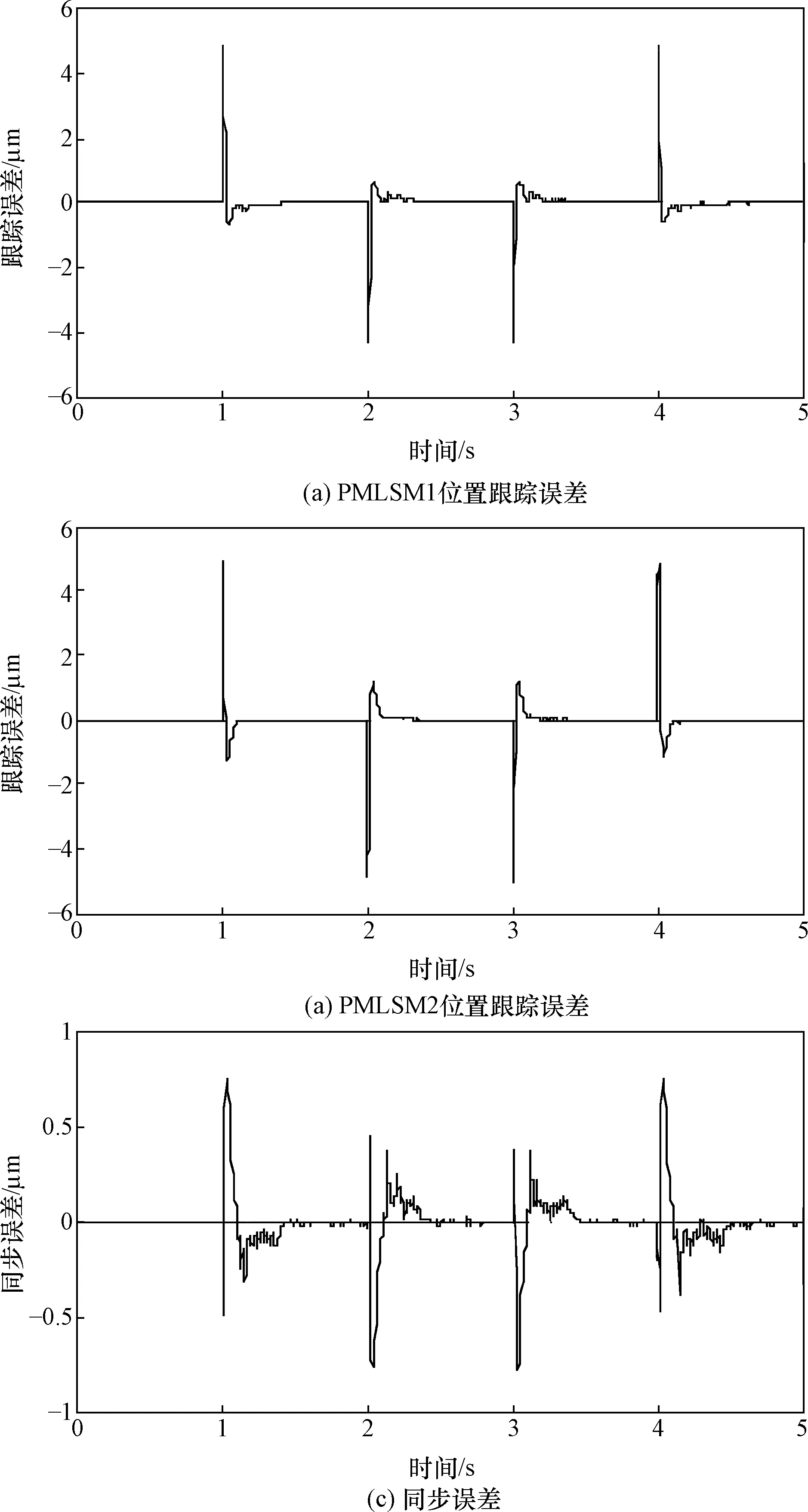
图6 基于TSKRFNN+CCC的双直线电机伺服系统位置跟踪误差及同步误差曲线Fig.6 Position tracking error and synchronization error curves of dual linear motor servo system based on TSKRFNN+CCC
4 结论
针对双直线电机中存在不确定性以及耦合现象的问题,提出一种TSKRFNN与交叉耦合控制相结合的同步控制方法。利用TSKRFNN强大的自学习能力,估计系统中不确定性并在线调整网络参数,保证单轴PMLSM伺服系统的控制性能。同时,将交叉耦合控制方法加入到双直线电机系统中以解决系统中存在的参数不匹配等耦合问题。仿真结果表明,该方法行之有效,可极大地削弱不确定性因素对系统的影响,从而实现双直线电机伺服系统的精准位置控制。
