四轮独立驱动FSEC 赛车稳定性控制*

宋成镖 李刚

（辽宁工业大学）

随着汽车技术的不断进步，关于车辆稳定性控制的研究也十分丰富[1]。在控制方法方面已经从最初的差动制动扩展到主动前轮转向控制、四轮转向控制、直接横摆力矩控制等[2]。应用控制理论从PID 控制、最优控制扩展到自适应控制、模糊逻辑控制以及人工神经网络控制等[3-5]。由于大学生电动方程式赛车是近几年兴起的[6]，对其稳定性控制方面的研究较少，但是由于其在安全性方面的重要作用，已逐渐被重视。为充分利用四轮独立驱动FSEC 赛车四轮力矩独立可控的优势，文章选取直接横摆力矩控制方式对赛车进行稳定性控制，配合目前最成熟，应用最为广泛的PID 算法，能够最大程度地保证控制算法的实时性，提升控制效果。

1 直接横摆力矩控制器搭建

直接横摆力矩控制器结构，如图1 所示。采用分层式结构，包括信号采集层、决策计算层、控制分配层和执行机构层。在信号采集层，模拟驾驶员操纵命令，通过PID 控制车辆的总驱动力矩，控制车速变化；决策计算层通过车速和驾驶员的转向盘转角输入，计算出目标横摆角速度，并与实际横摆角速度值做差，输入PID控制器，给出附加横摆力矩；控制分配层根据来自信号采集层的总目标驱动力和所需的附加横摆力矩，通过差动驱动规则对四轮驱动力进行分配；输出的4 个车轮的驱动力，通过执行机构层的四轮轮毂电机实现稳定性控制。

图1 横摆力矩控制原理图[7-8]

1.1 参考模型

线性二自由度车辆动力学模型能够很好地反映车辆的稳定性参数状态，并且在运算简便性与实时性方面具有一定优势[9-10]，因此被众多车辆操纵稳定性研究选为理想模型，如图2 所示。

图2 线性二自由度模型

根据模型可以看出，车辆稳定性问题可由车辆侧向运动与横摆运动表征，其微分方程为：

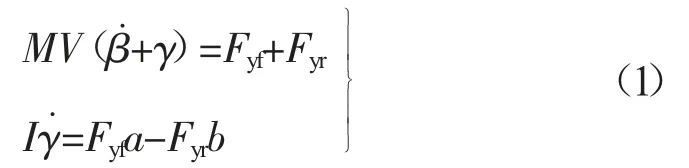
式中：M——汽车总质量，kg；

V——速度，m/s；

I——车辆绕Z轴的转动惯量，kg·m2；

Fyf——前轮的侧向力，N；

Fyr——后轮的侧向力，N；

β——质心侧偏角，rad；

γ——横摆角速度，rad/s；

a，b——重心与前、后轴之间的距离，m；

βf，βr——前、后轮胎侧偏角，rad。

设前后轮的侧偏刚度分别为Kf和Kr，并设Fyf和Fyr分别与前后轮的侧偏角βf和βr成正比，即轮胎在线性区工作，那么轮胎侧向力，如式（2）所示。

将式（2）代入式（1）中，并设前轮转角为 δf，另外在稳态转向条件下，车辆质心侧偏角β、横摆角速度γ 均不变，即可得：

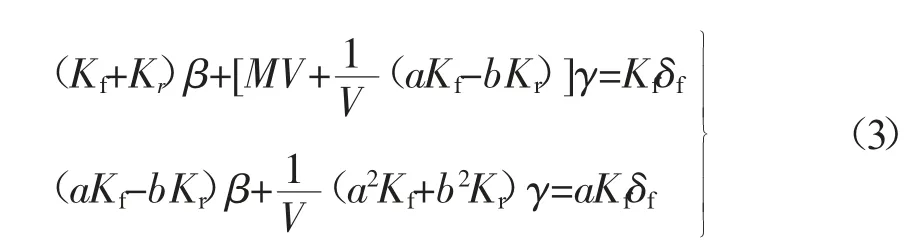
通过式（3）可知，表征车辆稳定性的参数是关于β，γ，δf，V的方程组，其中速度V与前轮转角 δf都由驾驶员控制输入，而质心侧偏角β 在实际车辆控制中获取较困难，因此最后选取横摆角速度表征车辆的稳定状态，关系为：

式中：K——稳定性因数，s2/m2。

1.2 横摆力矩决策控制器

通过上述对参考模型的分析可知，车辆的稳定性控制问题可用质心侧偏角与横摆角速度表征，但是实际车辆控制中质心侧偏角获取比较困难。另外，质心侧偏角不超过一定范围时，横摆角速度完全能够反映车辆的稳定性状态。因此文章选取横摆角速度为控制目标量。控制原理，如图3 所示。

图3 横摆力矩决策算法原理图

定义实际与理想横摆角速度偏差为：

所需附加横摆力矩为：

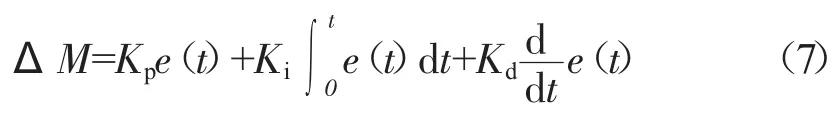
式中：e（t）——横摆角速度偏差，rad/s；

γ*——目标横摆角速度，rad/s；

γ——实际横摆角速度，rad/s；

ΔM——附加横摆力矩，N·m；

Kp，Ki，Kd——比例系数、积分系数、微分系数。

1.3 驱动力分配器

4 个车轮驱动力矩可通过各轮驱动电机的转矩换算得到：

式中：Fxi——某车轮驱动力，N；

Txi——某轮驱动力矩，N·m；

R——车轮滚动半径，m。

当车辆直线行驶时，四轮驱动力相等。当车辆转弯时，根据决策出的附加横摆力矩符号对车辆状态进行判断：当附加横摆力矩大于0 时，认为车辆需要逆时针的附加横摆力矩，此时应适当增大右侧车轮驱动力，减小左侧车轮驱动力；当附加横摆力矩小于0 时，认为车辆需要顺时针的附加横摆力矩，此时应适当增大左侧车轮驱动力，减小右侧车轮驱动力，具体的分配规则为：

当 ΔM=0 时：

当 ΔM＞0 时：

当 ΔM＜0 时：

式中：Ff1，Ff2，Fr1，Fr2——汽车左前轮、右前轮、左后轮、右后轮的驱动力，N；

B——轮距，m；

FTarget——油门请求驱动力，N。

2 仿真试验验证

2.1 CarSim 车辆模型建立

基于车辆动力学仿真软件CarSim 中的方程式赛车模型进行仿真试验，更新赛车参数并将传动系统与发动机系统用Simulink 模型代替，主要参数如表1 所示。

表1 基于CarSim 软件进行仿真试验的赛车参数情况

2.2 仿真试验

CarSim 与Simulink 联合仿真试验选取2 个典型的试验场景，分别是快速移线仿真试验与蛇形保持仿真试验。

2.2.1 快速移线仿真试验

车辆速度为70 km/h、高附着系数路面、闭环双移线转向控制，在70 m 时实施变道动作，向左移动3.5 m，随后变更回原来车道。试验结果，如图4 和图5 所示。

图4 快速移线仿真试验横摆角速度曲线

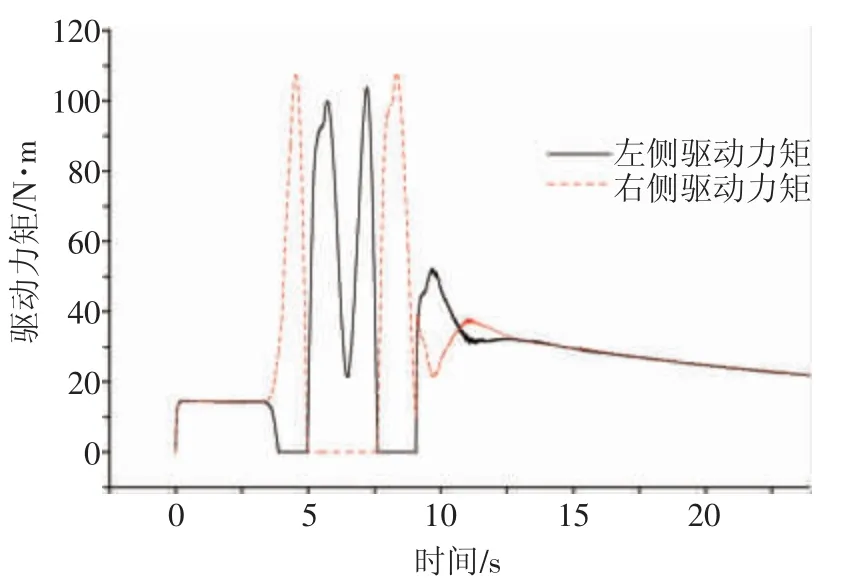
图5 快速移线仿真试验驱动力矩曲线

从横摆角速度仿真结果中可以看出，施加控制车辆可以较好地跟踪目标横摆角速度。从驱动力分配曲线可以看出，施加控制后车辆的左右侧车轮转矩差异明显，控制效果显著。

2.2.2 正弦保持仿真试验

车辆初始速度为80 km/h、高附着路面、闭环正弦转向输入，幅值1.5 m，每隔30 m 设置1 个桩桶作为参考标识。试验结果，如图6 和图7 所示。

图6 正弦保持仿真试验横摆角速度曲线

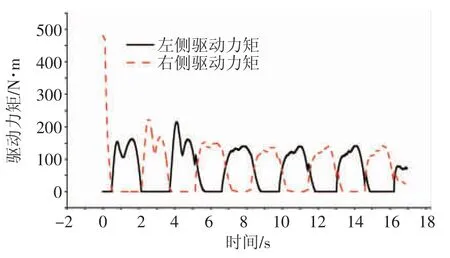
图7 正弦保持仿真试验驱动力矩曲线

从横摆角速度仿真结果可以看出，在频繁的转向输入下车辆已经不能很好地跟踪目标横摆角速度，但是相对于无控制车辆，施加控制的车辆依然能够在响应速度与跟踪幅度上占有一定优势。从驱动力分配曲线图可以看出，施加控制后，车辆的左右侧车轮转矩变化十分均匀，控制效果稳定。

3 结论

文章利用四轮驱动电动方程式赛车驱动力矩独立可控的优势，基于PID 控制理论设计直接横摆力矩稳定性控制算法，对驱动力进行合理分配，能够有效提升车辆操纵稳定性。选取双移线与正弦保持试验工况对算法进行仿真试验，结果表明施加控制的车辆能够较好地跟踪目标横摆角速度，实现车辆的良好控制。文章提出算法是建立在参考模型线性区间的，下一阶段应将非线性因素加入进来，建立更加完善的稳定性控制算法。