基于SPSS 竖直埋地换热器性能影响因素分析

赵宏

黑龙江省水利水电勘测设计研究院

0 引言

直接膨胀式地源热泵系统地埋管换热器是热泵与土壤换热设备，还充当蒸发器/冷凝器，其换热性能对整个地源热泵系统的能效起到决定性作用[1]。由于地下换热系统占用场地较大，钻井与回填的工作量也很大，在产品研发阶段进行大量试验研究存在很大困难，数值模拟是对这个复杂的两相流换热过程进行研究的重要方法。

文献[2-3]建立了修正的两相流混合物模型，对地下换热系统供热工况的三维流场和换热过程进行了数值模拟，发现工质参数（进口质量流量、干度、蒸发温度）对出口温度，出口总压恢复系数和出口蒸汽体积分数存在不同程度的影响。本文基于SPSS 统计软件通过方差分析的方法，检验进口工质参数对出口温度，出口总压恢复系数和出口蒸汽体积分数的影响程度。通过回归分析的方法求解进口工质参数对出口工况参数的相关模型。提出减小地下换热系统埋深的设计思路，并利用最佳工况效果多目标规划模型求解蒸发充分发展段最佳换热性能对应的工况参数。

1 因素敏感性分析

1.1 干度、质量流量对出口温度的影响

模拟计算中，干度取0，0.1，0.2，0.33，0.4，0.5 和0.6七个值，质量流量取0.009 kg/s，0.012 kg/s，0.015 kg/s，0.018 kg/s 和0.021 kg/s 五个值，分别对应计算出35 个出口温度。进口干度，质量流量和出口温度三者关系具体如图1 所示，出口温度随着干度的增加有一定的上升，出口温度随质量流量的变化规律不易直观获得。

通过双因素方差分析来检验干度和质量流量是否对出口温度存在显著影响。利用SPSS 软件分析得到结果如表1 所示：在0.05 的显著性水平下，干度对出口温度存在非常显著的影响（F=20.693，p＜0.05），而质量流量对出口温度不存在显著的影响（F=0.198，p＞0.05）。

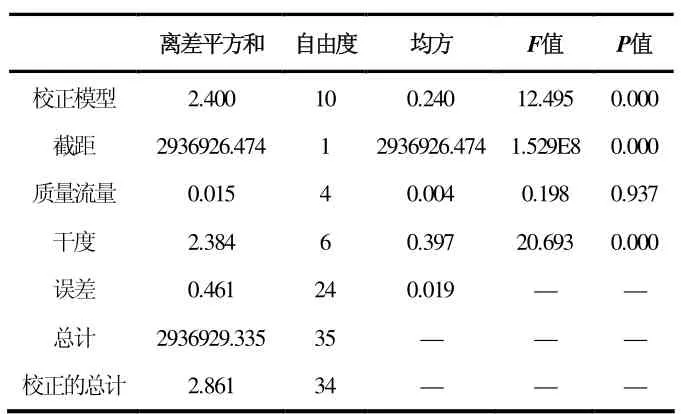
表1 干度和质量流量对出口温度的方差检验

1.2 干度，质量流量对总压恢复系数的影响

将干度取七个值，质量流量取五个值，得到对应的35 个出口总压恢复系数值，三者的变化关系如图2所示，随着干度、质量流量的增大，总压恢复系数减小，说明干度和质量流量对总压恢复系数存在较明显的影响。

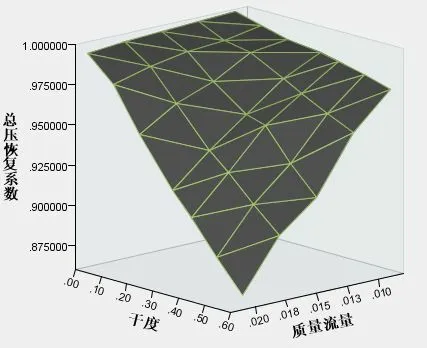
图2 干度，质量流量和总压恢复系数三者关系

通过SPSS 双因素方差分析检验干度和质量流量对总压恢复系数的影响，得到结果如表2 所示：在0.05的显著性水平下，干度（F=14.304，p＜0.05）和质量流量（F=15.227，p＜0.05）对总压恢复系数存在非常显著的影响。

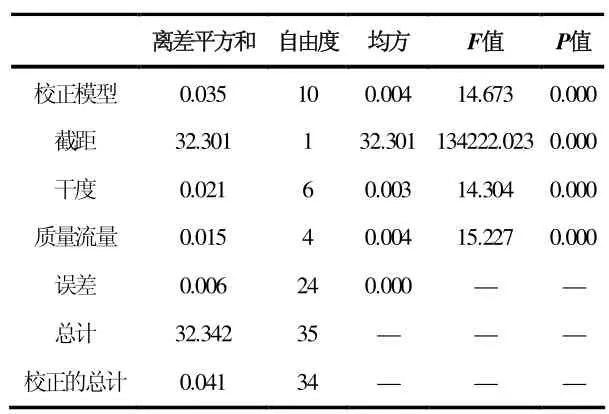
表2 干度和质量流量对总压恢复系数的方差检验

1.3 干度、质量流量对蒸汽体积分数的影响

将干度取七个值，质量流量取五个值，得到对应的35 个出口蒸汽体积分数值，三者的变化关系如图3 所示，随着干度增大，蒸汽体积分数呈现随之增加的变化规律。而随着质量流量增加，蒸汽体积分数基本保持不变。

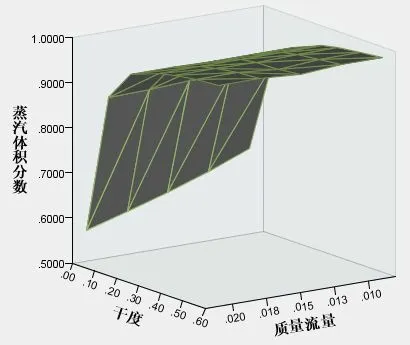
图3 干度，质量流量和蒸汽体积分数三者变化情况

通过SPSS 双因素方差分析检验干度和质量流量对蒸汽体积分数的影响，得到结果如表3 所示：在0.05的显著性水平，干度对蒸汽体积分数存在显著的影响（F=272.578，p＜0.05），而质量流量对蒸汽体积分数不存在显著的影响（F=1.211，p＞0.05）。

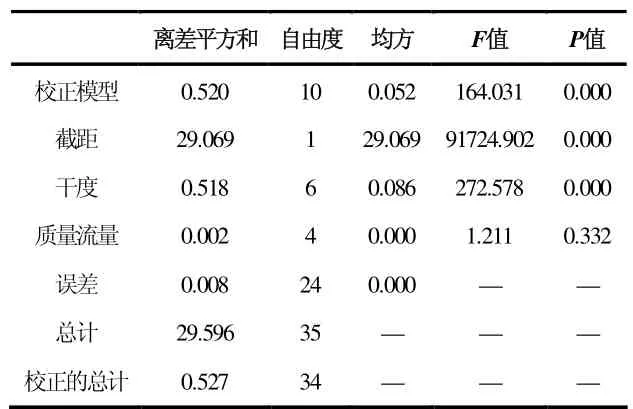
表3 干度和质量流量对蒸汽体积分数的方差检验

2 因素回归分析

通过敏感性影响分析已经了解到干度对出口温度，总压恢复系数和蒸汽体积分数都存在非常显著的影响，而质量流量只对总压恢复系数存在显著的影响，下面通过回归分析的方法找出各因素对出口温度，总压恢复系数和蒸汽体积分数的影响规律。

2.1 干度对出口温度的回归分析

由图1 可以看出随着干度的增加，出口温度并不是呈现出线性增长规律。因此将干度作为自变量，出口温度作为因变量，通过二次回归模型，三次回归模型和增长模型分别进行拟合，对比三者拟合效果，从而得到干度对出口温度的影响模型。通过SPSS 回归分析得到结果如表4，三个模型都通过了显著性检验，都可以用来表示干度与出口温度之间关系。三个模型的F 值非常接近，三次模型的R2值最高，说明三次模型更加接近原始数据的变化规律。故选择三次模型作为干度与出口温度的拟合模型，即：

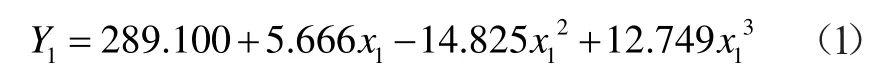
式中：Y1为出口温度，x1为干度。

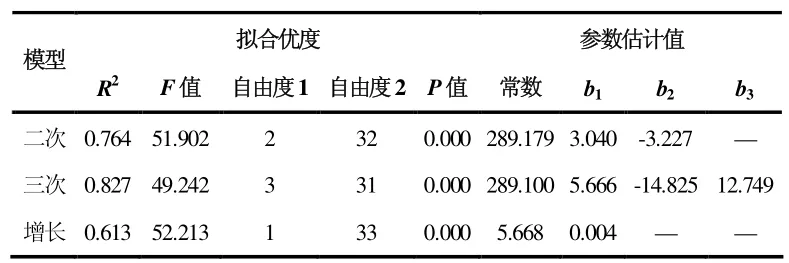
表4 干度对出口温度的回归模型检验

2.2 干度、质量流量对总压恢复系数的回归分析

在因素敏感性影响分析中，知道干度和质量流量对总压恢复系数都存在非常显著的影响，将这两个因素同总压恢复系数建立多元回归模型。结合图2 可知，随着干度、质量流量的变化，总压恢复系数呈现出近似线性的变化，因此建立多元线性回归模型。考虑到干度和质量流量之间可能存在多重共线性，采用SPSS逐步回归法进行分析，得到结果如表5、表6：通过两次迭代分别选择干度、质量流量进入模型，得到的回归模型的F 值统计量为95.597，对应的概率P 值小于显著性水平0.05，说明模型可以用来表示干度，质量流量和总压恢复系数之间的关系。

表5 多元回归模型方差检验表

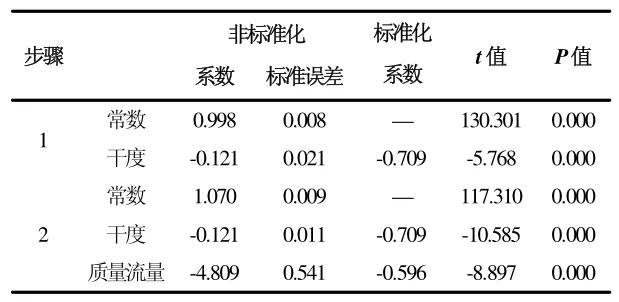
表6 多元回归模型参数检验表

模型参数检验显示，干度和质量流量对总压恢复系数都呈现显著的负作用，即随着干度、质量流量的增加，总压恢复系数会不断降低。得到干度，质量流量与总压恢复系数的多元线性回归模型：

式中：Y2为总压恢复系数，x2为质量流量。

2.3 干度对蒸汽体积分数的回归分析

图3 显示，随着干度的不断增加，蒸汽体积分数也呈现逐渐增大的趋势，但是增大速度在不断减缓，并且蒸汽体积分数越来越接近于1。选择二次，三次和增长模型与Logistic 回归模型进行对比，如图4 所示，通过SPSS 回归分析得到分析结果见表7。

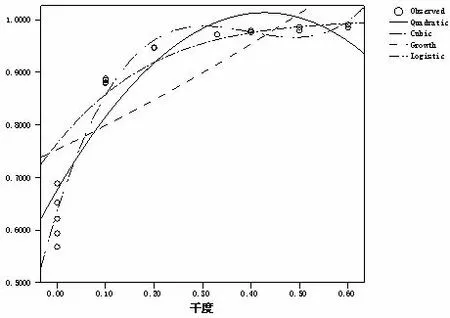
图4 干度与蒸汽体积分数的四种拟合模型对比

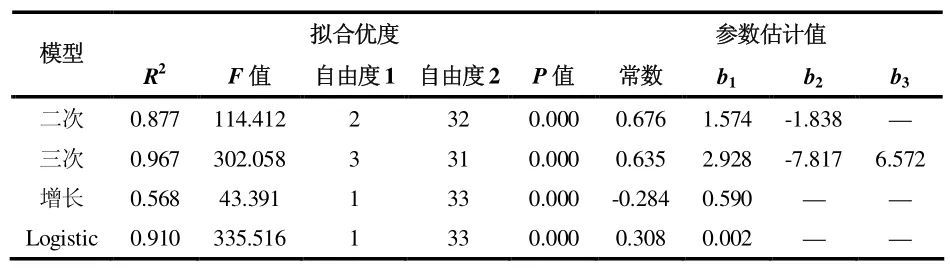
表7 干度对蒸汽体积分数的回归模型检验

干度与蒸汽体积分数的回归模型检验结果显示，二次，三次，增长和Logistic 回归模型的方差检验都通过显著性检验。从模型拟合优度检验可见，三次和Logistic 模型拟合的最好，其中三次模型的R2大于Logistic 模型，而Logistic 模型的F 值大于三次模型，说明三次模型对原始数据拟合更好，而Logistic 模型更能接近原始数据的变化特征，当干度大于0.6 时，三次模型预测蒸汽体积分数将大于1，出现非物理现象，而Logistic 模型预测随着干度的不断增加，蒸汽体积分数将不断接近、且不超过于1，符合实际。因此选择Logistic 模型来表示干度与蒸汽体积分数之间的关系：

式中：Y3为蒸汽体积分数。

2.4 进口温度对出口温度，总压恢复系数和蒸汽体积分数的回归分析

质量流量0.012 kg/s、干度0.33 工况下，进口蒸发温度与出口温度、总压恢复系数、蒸汽体积分数的关系，如图5 所示：随着进口温度的不断增加，总压恢复系数和出口温度基本呈现出线性增长，而蒸汽体积分数随着进口温度的变化基本保持不变。分别建立进口温度与出口温度、总压恢复系数、蒸汽体积分数三个线性回归模型，利用SPSS 回归分析得到结果如表8、表9 所示。

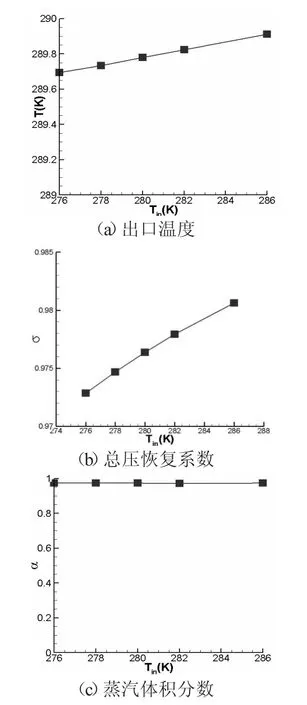
图5 进口温度与出口温度、总压恢复系数、蒸汽体积分数的关系

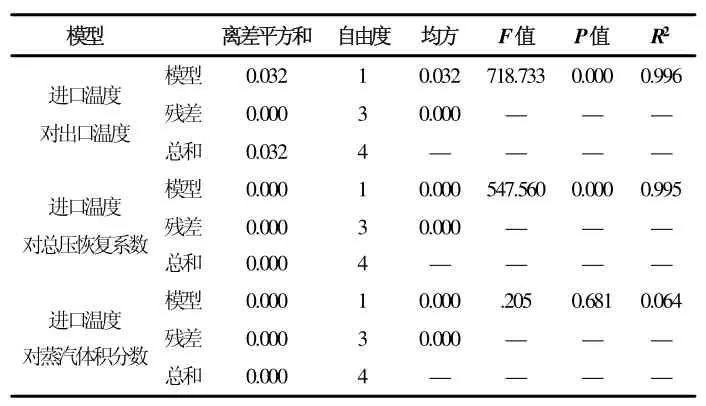
表8 回归模型方差检验表

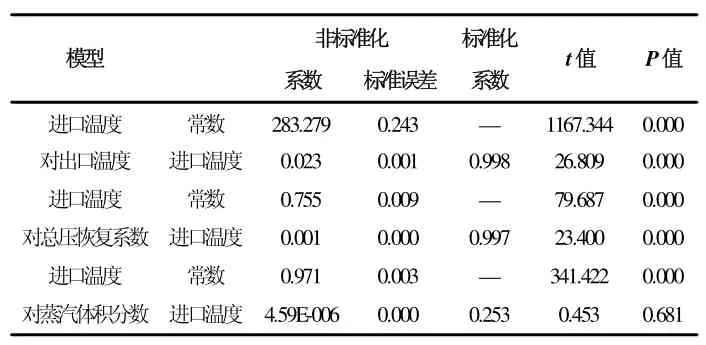
表9 回归模型参数检验表

从模型参数检验结果可知，进口温度对出口温度（β=0.998，p＜0.05）、总压恢复系数（β=0.997，p＜0.05）存在非常显著的影响，对蒸汽体积分数不存在显著影响（β=0.253，p＞0.05）。得到进口温度对出口温度、总压恢复系数两个线性模型分别为：

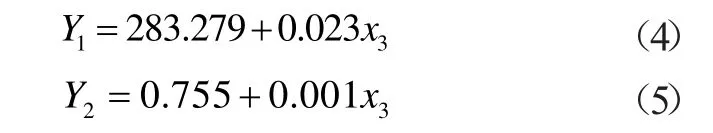
式中：x3为进口温度。

上述各因素的回归分析可知各个因素对出口温度、总压恢复系数和蒸汽体积分数的影响大小：干度对出口温度、总压恢复系数和蒸汽体积分数均存在显著影响，其中干度对蒸汽体积分数的影响最大，其次是对出口温度的影响，影响最小的是总压恢复系数。质量流量对总压恢复系数存在显著影响，判定系数为0.355，对出口温度和蒸汽体积分数没有显著的影响。进口温度对出口温度、总压恢复系数的判定系数分别为0.996、0.995，对两者的影响显著性也非常接近，对蒸汽体积分数不存在显著的影响。

3 蒸发充分发展段的最佳换热工况对应进口参数求解

文献[3]计算发现，对于几何结构如文献[4]中的U型埋地铜管换热器而言，温升主要集中在进口0～15 m管段。对U 型铜管进口段的换热特性计算可知，通过对进口工质参数的控制，在管程5 m 处蒸汽体积分数可高达0.975，判断相变换热基本完成。故本文提出减小地下换热系统设计埋深的想法，并将进口段（U 型铜管进口0～5 m）定义为蒸发充分发展段。

基于多目标规划模型，求解蒸发充分发展段的最佳流动换热工况下的工质进口参数工程。根据上文求得干度、质量流量、进口温度三个影响因素与出口温度、总压恢复系数、蒸汽体积分数之间的关系表达式，结合各影响因素的变化范围，设定目标函数和约束条件，约束条件参考国内外相关学者的研究及计算经验[4-5]给出，具体如下：

目标函数：

①出口温度越高越好：max=Y1；

②总压恢复系数越接近1 越好：min=1-Y2；

③蒸汽体积分数越接近1 越好：min=1-Y3。

约束条件：

①干度值在0～0.4 范围内：0＜x1＜0.4；

②质量流量在0.005～0.03 范围内：0.005＜x2＜0.03；

③进口温度在270～285 范围内：270＜x3＜285；

④总压恢复系数和蒸汽体积分数都不能大于1：Y2＜1、Y3＜1。

将上述多目标规划模型输入到LINGO 软件中，因蒸发充分发展段仅是U 型地埋铜管的进口支管的靠近地表部分，设置目标②的权重为10，目标①和③的权重设置为1，得到：当干度x1=0.4、质量流量x2=0.03 kg/s、进口温度x3=283.28 K 时，三个目标达到最优，蒸发充分发展段出口温度Y1=288.9721 K、总压恢复系数Y2=0.9103、蒸汽体积分数Y3=0.9658。

4 结论

1）基于SPSS 统计软件通过方差分析的方法，检验进口工质参数对出口温度，出口总压恢复系数和出口蒸汽体积分数的影响程度，通过回归分析的方法求解了进口工质参数对出口工况参数的相关模型，即在0.05 的显著性水平下，Y1=289.100+5.666x1-14.825x12+12.749x13；Y2=1.070 -0.121x1-4.809x2；Y3=1/(1 +0.308 ×0.002x1)。求解了进口温度对出口温度、总压恢复系数两个线性模型：Y1=283.279+0.023x3；Y2=0.755+0.001x3。

2）利用了LINGO 软件中最佳工况效果多目标规划模型求解了蒸发充分发展段最佳换热性能对应的工况参数，即当进口干度x1=0.4、质量流量x2=0.03 kg/s、蒸发温度x3=283.28 K 时，换热及流动性能达到最优，出口温度Y1=288.9721 K、总压恢复系数Y2=0.9103、蒸汽体积分数Y3=0.9658。