惠西南地区储层含油气性叠前地震固液解耦识别*

宗兆云 孙乾浩 陈维涛 罗 明 贾培蒙 何 叶 卫 哲

（1.中国石油大学（华东）地球科学与技术学院 山东青岛 266580； 2.中海石油（中国）有限公司深圳分公司 广东深圳 518054）

珠江口盆地惠西南H1地区油气资源丰富，具有多源供烃、多层系含油的特点［1］。其中，惠西南地区位于珠江口盆地珠一坳陷惠西半地堑西南侧，是东沙隆起向珠一坳陷的延伸地带，以构造-岩性复式圈闭勘探为主，产量主要来自珠江组三角洲沉积体系，油气层为K08—K22。由于该工区叠前数据主频较低（约25 Hz）、大角度叠前数据信噪比低且目标砂体纵向变化大、岩性圈闭边界难落实，复式油气藏延展范围难落实，常规的流体识别方法难以排除因孔隙度造成的假“亮点”。

地震岩石物理理论搭建了地震资料与弹性参数之间的桥梁，为利用叠前地震资料进行储层流体识别奠定了理论基础。地震岩石物理驱动的叠前地震流体识别方法是当今勘探地球物理领域中储层含油气性判别的主流方法［2-6］。该方法将与孔隙流体有关的特性表征为流体指示因子，或者基于地震岩石物理构建流体类型与弹性参数的量化关系，并利用地震资料所包含的丰富信息实现流体指示因子的反演或预测［7］，从而达到储层油气识别的目的。

针对常规地震反演方法对孔隙流体类型判别精度低的问题，首先基于目标储层砂体岩石骨架结构、孔隙性质以及流体分布特征，建立了相应的砂泥岩油气储层地震岩石物理模型。其次，基于岩石物理分析结果，优选固体解耦等效流体体积模量作为流体指示因子。最终，推导相应的地震反射特征方程，实现了岩石物理驱动固液解耦油气直接识别。该方法能够有效避免因岩石骨架孔隙度等物性因素导致的流体识别假象，提高叠前地震孔隙流体判识的精度，降低油气勘探开发的高风险。

1 地震岩石物理研究

1.1 地震岩石物理建模

惠西南H1地区的K08—K22储层为砂泥岩储层，在地震岩石物理建模过程中存在以下3个问题：①输入矿物模量未知；②泥岩段缺少孔隙度解释；③Xu-White模型干燥岩石孔隙纵横比不变。本文采用3种策略解决相应的问题：①建立岩石弹性模量与岩石物性参数关系式，使饱和岩石模量误差最小，得到最优矿物组分模量，对相同层位进行多井统计估算；②利用测井数据约束反演孔隙度；③利用DEM模型［8-10］和K-T模型［11］建立变孔隙纵横比的干燥岩石。改进的砂泥岩模型除考虑了砂岩和泥岩影响，考虑到实际岩石中的孔隙纵横比不是固定的，形成了一套变孔隙纵横比的碎屑岩地震岩石物理模型来计算岩石的宏观弹性模量（图1）。

图1 基于岩石物理模型的岩石弹性模量估算Fig.1 Estimation of elastic modulus based on rock physical model

在惠西南H1地区复杂含油气储层岩石物理模型构建的基础上，利用已有的测井解释曲线，如矿物含量、孔隙度、泥质含量以及含水饱和度等，采用测井约束反演修正方法对靶区的横波速度数据进行估算，并与实测横波数据进行对比来验证岩石物理模型的合理性和有效性。针对不同岩性的目标储层，选择性地采用相应的模型来实现关键井的横波速度估算。图2为W1井纵横波速度估算结果，可以看出，本方法预测的横波速度与实测的横波速度吻合很好，说明该岩石物理模型的合理性。同时发现在目标层处仍能够预测较为准确的纵波速度和横波速度，预测误差大概在10%以内，在可接受范围内。

1.2 岩石物理分析

基于1.1节构建的地震岩石物理模型，对H1地区进行多参数岩石物理交会分析，选出几个较好的弹性参数作为备选参数，对工区内W1井的岩性进行交会分析。图3为不同弹性参数交会分析结果，可以看出，砂岩显示为低弹性阻抗（小角度部分叠加）和低密度，泥质砂岩显示为较低的弹性阻抗，2个参数都可以区分砂岩和泥质砂岩，并能识别砂岩，为开展弹性阻抗反演提供了岩石物理理论支撑。图4为W1井的流体参数交会分析结果，可以看出，固液解耦等效流体体积模量Kf能够区分水层和油层。

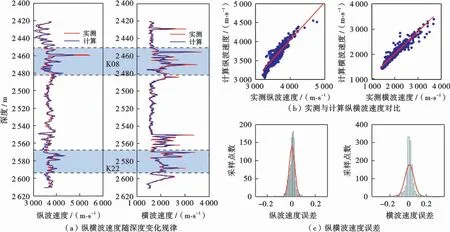
图2 H1地区W1井纵横波速度估算结果Fig.2 Results of the estimated P-wave and S-wave velocity of Well W1 in H1 area

图3 H1地区W1井不同弹性参数交会结果Fig.3 Intersection results of different elastic parameters of Well W1 in H1 area

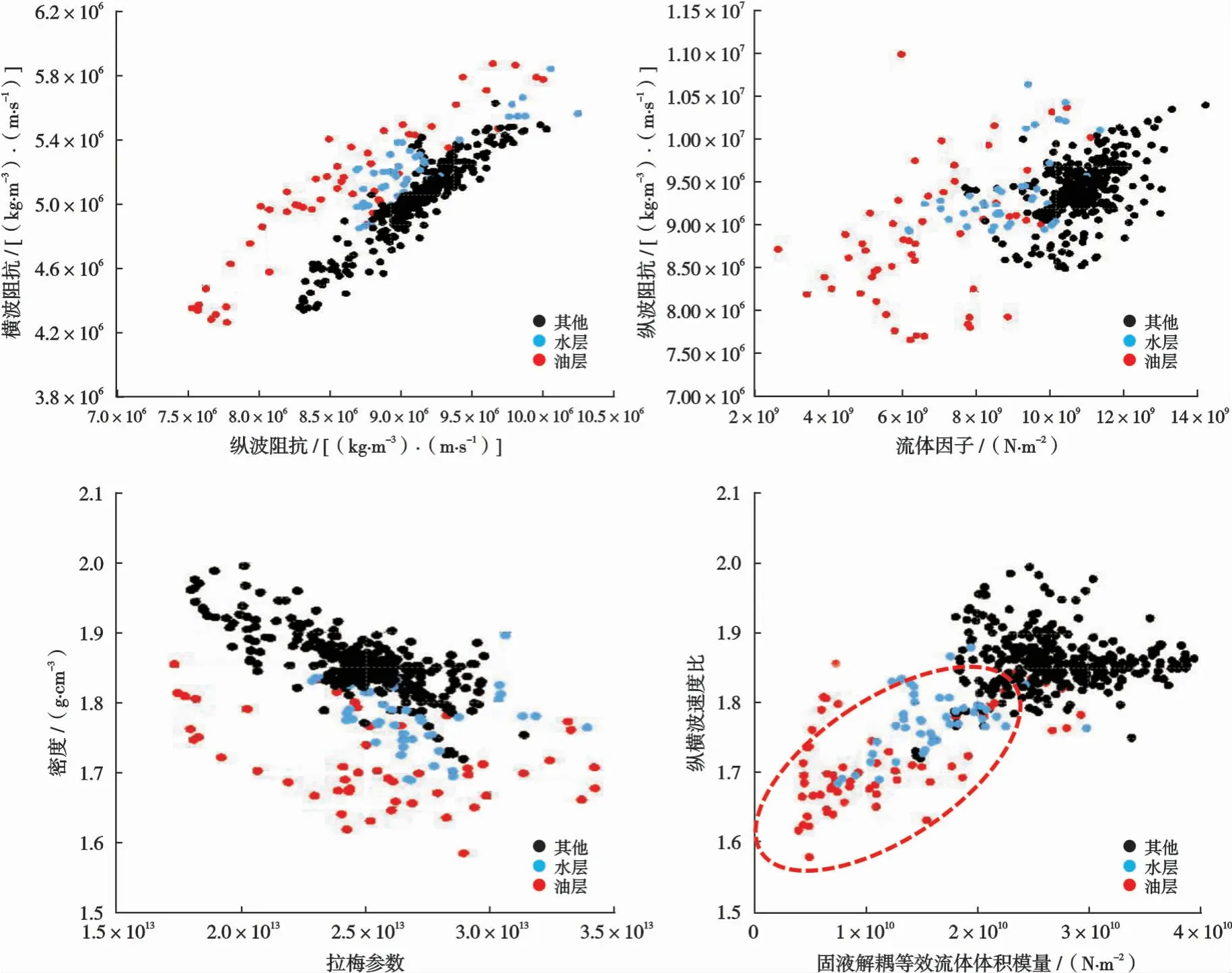
图4 H1地区W1井不同流体参数交会结果Fig.4 Intersection results of different fluid parameters of Well W1 in H1 area

1.3 储层敏感性参数分析

针对惠西南H1地区的优质储层评价领域，成熟油区目前以构造-岩性复式圈闭勘探为主，常规的地震勘探手段往往不够可靠稳定。首先需要选择对目标储层流体反映敏感的弹性参数，这对储层预测和流体识别意义重大，选定合适的参数可以减小地震优质储层评价的不确定性和多解性。图5对W2井弹性参数和储层物性参数进行了对比分析，弹性参数：①K22层油气砂体VP降低明显；②K22层弹性参数稳定；③密度明显降低；④固液解耦等效流体体积模量Kf递低（渐变模式）。储层物性：①K22层有效孔隙度约8%～20%；②K22层水饱和度10%～95%；③K22层气层物性较好。

一般情况下，流体类型的检测具有多解性，因此，需要选择对流体敏感性高的弹性参数作为流体指示因子。此处，利用测井中横波信息，对目标工区的弹性参数进行流体敏感性分析，流体的敏感性可根据下式计算：

式（1）中：Λf表示弹性参数对流体的敏感系数；m气为含气层的弹性参数值；m水为含水层的弹性参数值；s气为含气层的弹性参数标准差。

目标工区的流体敏感性分析结果如图6所示，IS为横波阻抗，VS为横波速度，λρ为拉梅参数和密度的乘积，μρ为剪切模量与密度的乘积，f为Gassmann孔隙流体项，σ为泊松比，VP为纵波速度，IP为纵波阻抗，Kf为固液解耦等效流体体积模量。通过流体敏感性对比分析可知，固液解耦等效流体体积模量Kf在区分水层和气层方面具有最大的潜力。

图5 H1地区W2井弹性参数和储层物性参数分析Fig.5 Analysis of elastic and physical parameters of Well W2 in H1 area

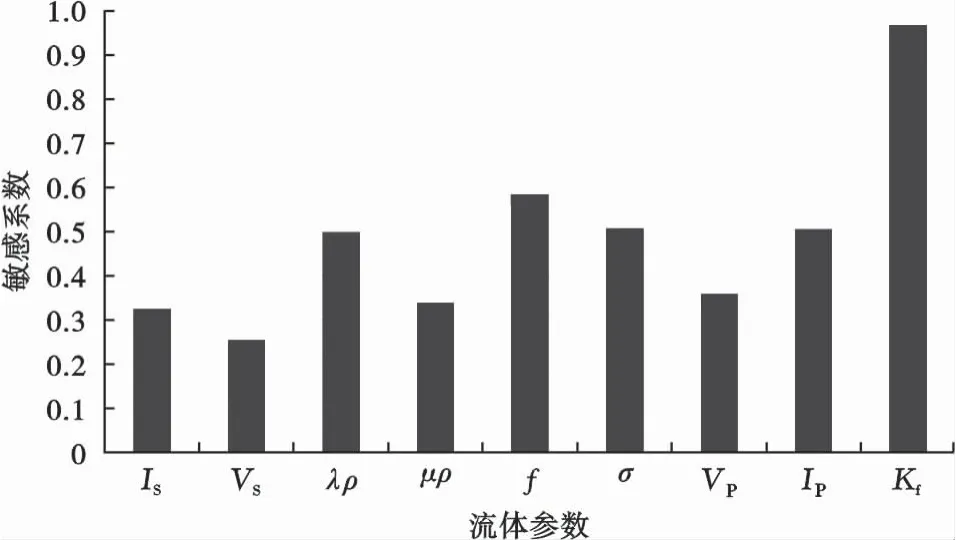
图6 H1地区地震岩石物理流体参数敏感性对比分析Fig.6 Comparative analysis of sensitive of the rock physical fluid parameters in H1 area

2 固液解耦等效流体体积模量直接提取

基于构建的地震岩石物理模型，对含流体储层进行正演模拟分析，获取流体的地震响应特征，并将这种响应特征表征为流体指示因子，用于地下储层流体类型的识别。因此，构建物理意义明确且对流体敏感性高的流体指示因子具有重要意义。

双相介质理论因其能够更好地表征孔隙流体的弹性特征而被广泛应用于流体识别中。Russell等在消除了密度项的影响后［12］，直接给出Gassmann流体项f的表达式，即

式（2）中：Kd为岩石骨架的体积模量，Ks为岩石基质的体积模量，Kf是固液解耦等效流体体积模量，对于有多相流体则可以利用Wood公式进行计算，计算公式为，Ko、Kg和Kw分别表示油、气和水的体积模量；So、Sg和Sw分别表示含油、气和水饱和度，且Sw+So+Sg=1。

通过分析式（2）可以发现，Gassmann流体项f不仅与流体的弹性特征有关，还受岩石固体参数（刚性参数）的影响，例如，矿物基质模量、干岩骨架模量以及孔隙度等，即固体相和液体相的弹性特征是耦合的。Dehua Han和Batzle等［13］利用统计岩石物理对碎屑岩进行了分析，研究了Biot-Gassmann理论中孔隙流体与岩石骨架间的耦合关系，将固液解耦等效流体体积模量Kf从耦合关系中解耦出来得［4］

基于临界孔隙模型的岩石物理经验公式［13-15］，得AVO线性近似公式为［4］

式（5）中：fm=φμ为固体刚性参数；γ2dry与γ2sat分别为干岩石与饱和岩石的纵横波速度比的平方；Kf为介质的固液解耦等效流体体积模量；μ为介质的剪切模量；ρ为介质的密度；φ为介质的孔隙度。借鉴Connolly推导弹性阻抗的思想［16］，用弹性阻抗表示为

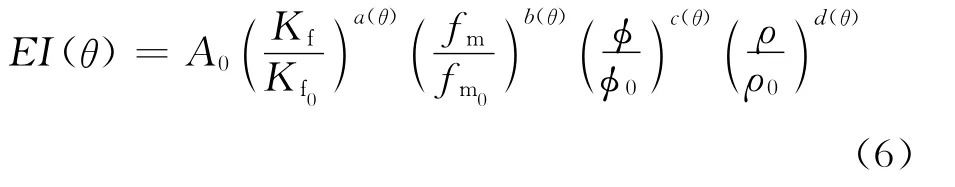
式（6）中：A0是标准化因子，具体表达式为

由式（7）可知，当入射角θ=0时，弹性阻抗与波阻抗的值相等，当入射角非零时，弹性阻抗数值发生变化，但其量纲仍然与波阻抗保持一致，为后续参数提取提供了保证。

弹性阻抗数据体的获取是弹性参数提取第一步，通常弹性阻抗数据体可通过常规的叠后地震反演来获取，获得弹性阻抗数据体后，需要利用式（6）对弹性参数进行提取。经过标准化的弹性阻抗方程如式（6）所示，为了简化求解方法，对公式进行对数变换，将其转化为线性形式［7］

其中：EI0=A0。

根据式（8），在获得弹性阻抗数据体以及孔隙度数据体时，利用

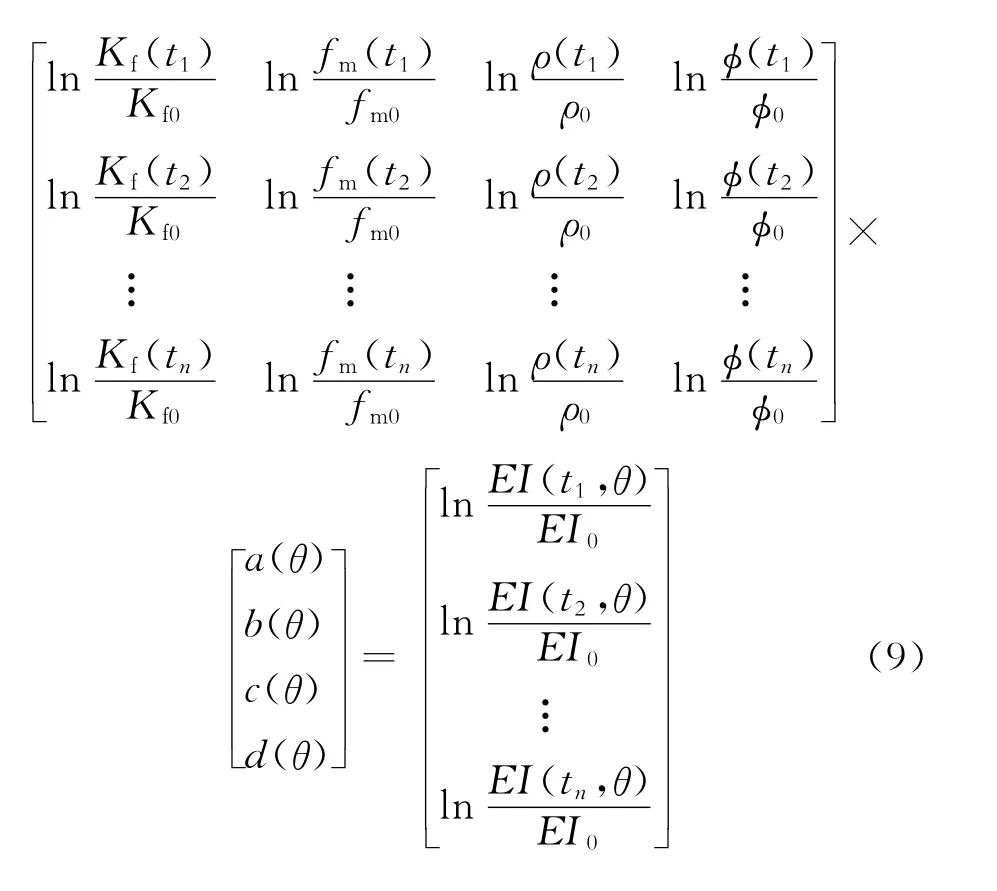
求解以上矩阵，即可获得适用于研究工区的系数a（b）、b（θ）、c（θ）和d（θ）的数值，n为每一道对应的参数个数。针对不同的入射角度分别计算，便可得到4个角度（分别为θ1、θ2、θ3和θ4）对应的16个系数，即a（θ1）、b（θ1）、c（θ1）、d（θ1）；a（θ2）、b（θ2）、c（θ2）、d（θ2）；a（θ3）、b（θ3）、c（θ3）、d（θ3）；a（θ4）、b（θ4）、c（θ4）、d（θ4）。

将16个系数代入方程组（10），可得到任意采样点处的固液解耦等效流体体积模量、固体刚性系数以及密度参数。

3 实例应用

为了避免通过纵、横波速度间接计算导致的误差累积，基于式（6）开展了固液解耦等效流体体积模量直接提取的弹性阻抗反演方法。图7为过6口井的部分角度叠加地震剖面。A井K08层为干层，K22up层为气水界面，K22为油层；B井K08层为含气水层，K22up层为差气层，K22为气层；C井K08层为油水，K22层为含油水层；D、E、F井发育气层。

图8为弹性阻抗的反演结果，可以看出弹性阻抗在6口井储层发育位置显示出明显的低值异常，砂岩显示低值异常，弹性阻抗会随着泥质含量的增高而增高，泥质砂岩弹性阻抗值较砂岩和含泥砂高。 图9为反演的弹性阻抗直接提取的固液解耦等效流体体积模量剖面，可以看到含气区显示明显的低值，含油区低值程度次之，含水区低值程度较弱，这一结果与测井解释结果吻合，证明基于固液解耦等效流体体积模量的叠前地震直接提取方法不仅可以有效识别储层，还可以识别流体类型。

图7 H1地区部分角度叠加地震剖面Fig.7 Seismic profile of partial angle stack of H1 area

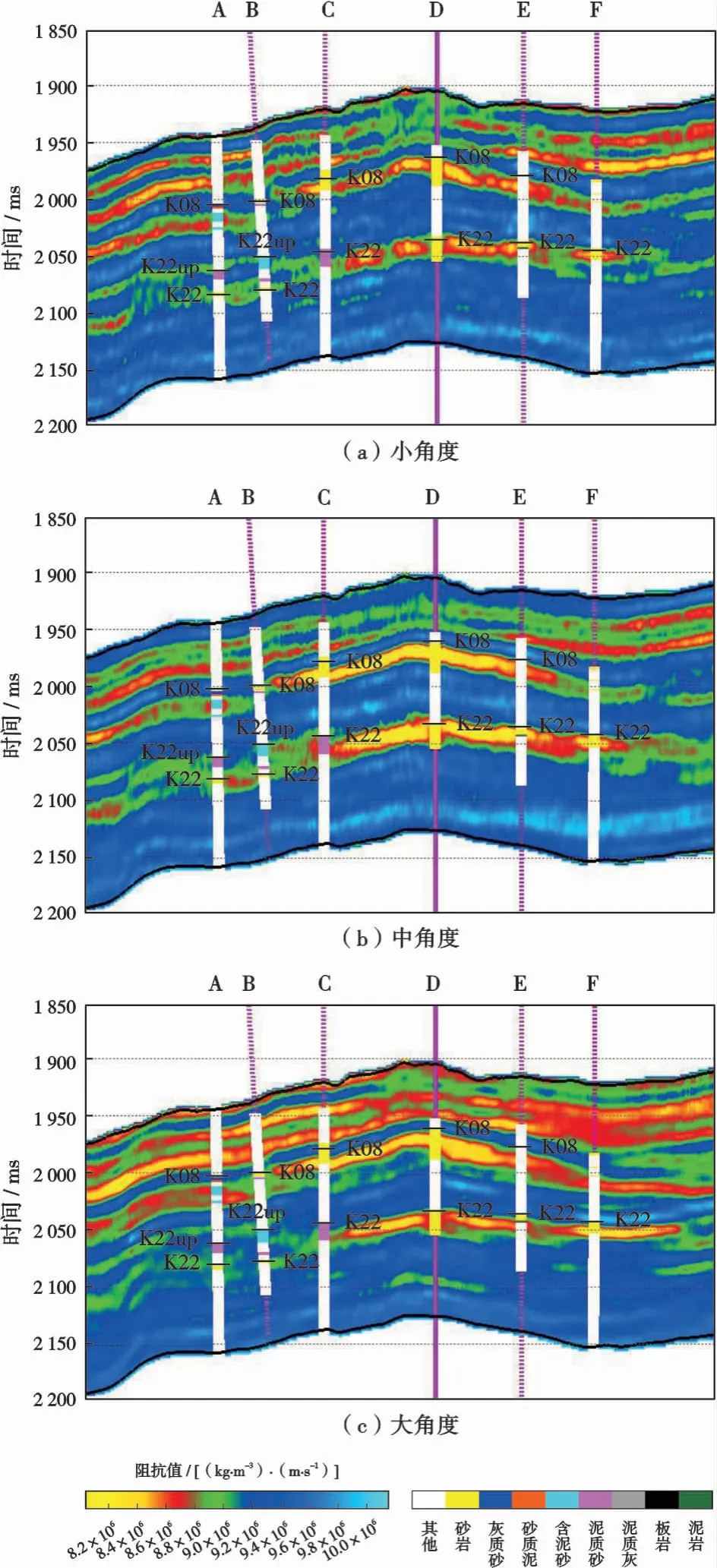
图8 H1地区弹性阻抗剖面Fig.8 Elastic impedance of H1 area

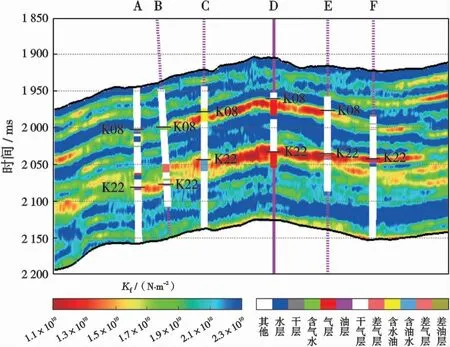
图9 H1地区固液解耦等效流体体积模量剖面Fig.9 Profile of solid-liquid decoupling fluid factor of H1 area

图10为沿K22层提取的小角度弹性阻抗均方根切片，为H1地区储层砂体展布范围。图11为沿K22层提取的固液解耦等效流体体积模量均方根切片，为预测的流体展布范围。可以看出，惠州D井区域有较强的能量响应，发育大范围储层并具有含流体性，与实际钻井结果吻合。惠西南地区发育部分储层，具有一定的含流体性。预测结果与地质认识吻合，证明了该方法对于储层刻画和流体识别的有效性。

图10 H1地区沿K22层提取的小角度弹性阻抗均方根切片Fig.10 RMSslice of small angel elastic impedance along K22 layer of H1 area

图11 H1地区沿K22层提取的固液解耦流体因子均方根切片Fig.11 RMSslice of solid-liquid decoupling fluid factor along K22 layer of H1 area

4 结论

1）在分析该工区岩石物理特征的基础上，构建了符合工区特点的变孔隙度砂泥岩岩石物理模型，并采用了基于测井约束反演修正的横波预测技术进行横波预测，预测横波与实测横波吻合，证明岩石物理模型的有效性。

2）通过地震岩石物理交会分析，对不同参数的岩性以及流体敏感性进行分析，认为小角度弹性阻抗和固液解耦流体因子可作为敏感性储层和流体参数，为储层描述和流体识别工作提供了有力支撑。

3）本文基于弹性阻抗利用直接反演的思想，实现了固液解耦流体体积模量的直接提取。该方法综合利用了地质信息、测井数据以及叠前地震AVO信息，既保证了常规弹性阻抗反演的抗噪性，又避免了间接反演的误差累积和孔隙度等物性的影响，可以更有效地识别储层及流体类型。