大伙房水库供水调度规则制定研究

2020-08-03王振辉

黑龙江水利科技 2020年7期

王振辉

(辽宁省丹东水文局，辽宁丹东 118001)

0 引言

优化算法与计算机技术的快速发展，推动了水库调度优化及模拟的研究，经模型演算后大多数水库均可获取适用的调度规则。

当前，水资源配置中的水库调度规则模块已被成功应用于多个商业软件，例如SPWATER、MIKE BASIN、HEC-ResSim、RIBASIM等软件，而获取水库调度规则的有关研究还比较少。智能算法的快速发展为获取水库调度规则提供了技术支撑，更多的智能算法逐渐得到应用，如Shiau[1]、Chang[2]、Chen[3]、Wang[4]等为获取更加合理的调度规则，深入探究了遗传及协同演化算法；尹正杰[5]等在制定调度规则时充分考虑了各行业用水信息，结合供水调度制定合理的运行机制；张双虎[6]等将遗传算法与差分演化算法相结合，以乌江水库群优化调度为例构造了梯级发电量最大的目标函数；黄家文[7]等综合应用免疫粒子群算法、水库蓄供水控制线和判别系数法，合理优化了蓄供水控制线。水库供水调度图为以往学者相关研究中最实用、最常见的调度规则，将优化与模拟相耦合形成了一套获取调度图的混合式方法。然而，在提取调度图过程中发现粒子群算法易陷入局部最优，模拟过程中该算法存在一定缺陷，为达到较优的结果求解时设定的迭代次数或粒子数一般较大[8]。

鉴于此，以大伙房水库为例，为制定合理的水库调度规则提出了混沌粒子群算法，通过实证分析验证了其可靠性与适用性。

1 水库供水调度模型

1.1 调度模型供水规则

设定用水户A、B、C为水库的供水对象，为便于调度分析设供水保证率最高者为A、最低者为C、用水户B居中。图1为调度图，按照设计供水保证率高低与供水目标的优先等级，将兴利库容分解为多个调度区并自下而上依次排列限制线。其中，调度图中时间和蓄水位不具备真实的意义，仅代表水库蓄水位随时间的变化规律。

水库运行过程中对每个用水户的供水规则，见表1，应充分考虑各调度区与水库蓄水量间的关系。

1.2 目标函数

1)设N、T为用水户数和水库供水的时段数，用水户i在时段t的缺水量、需水量和供水量△DEi(t)、WDi(t)、WSi(t)，则缺水量最少的目标函数可表示为：

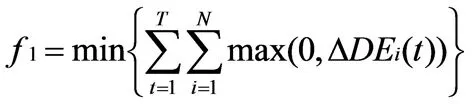
(1)

式中：△DEi(t)=WDi(t)-WSi(t)；∀t∈T，∀i∈N。

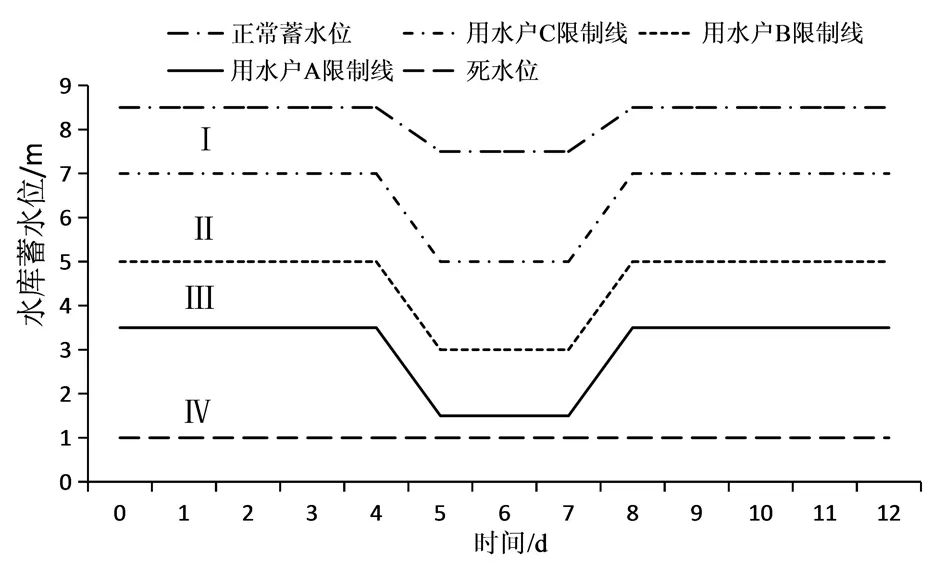
图1 水库运行调度图

表1 水库供水规则

2)引入Pi、Ratioi为用水户i的设计供水保证率和实际保证率，引入指标Mi(t)描述用水户i供水是否满足，则供水保证率最高的目标函数为：

新课程标准要求学生学习的数学内容必须是有挑战性的，有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动。教材把表内乘法分为两部分，第一部分主要是乘法算理理解以及2～6的乘法口诀，第二部分是7～9的乘法口诀，这样的编排不利于学生的思维连续性。有必要对表内乘法进行改进。要根据学生已有的认知特点，对教材进行适当的重组和补充，积极探索。

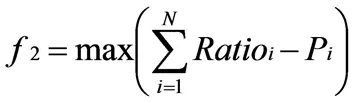
(2)

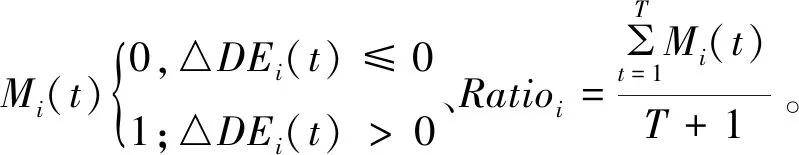
1.3 决策变量

实际上水库供水调度图上的各控制水位线就是决策变量，因此结合限制供水系数及水库蓄水状态，可以将调度图概化为以下表达式：

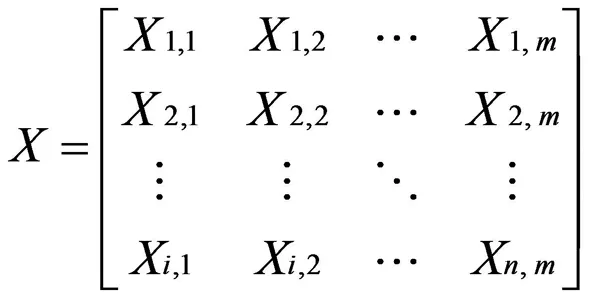
(3)

式中：m、n为单条调度线点数和调度线条数；Xi,j为调度线i上点j的控制水位。

1.4 约束条件

水量平衡、水库库容为水库调度模型的主要约束条件，此外涉及水库供水时还要考虑供水约束，各类约束的具体表达式为：

1)水量平衡约束条件。引入I(t)、L(t)为t时段入库水量与水库损失水量，S(t)、EC(t)为t时段水库的弃水量和坝下水环境需水量，S(t)、S(t+1)为t时段的初、末库容，以上各参数单位为万m3。因此，水库水量平衡约束可表示为：

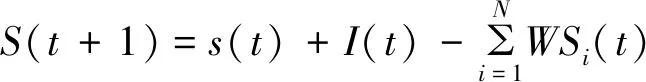
(4)

2)水位约束条件。设定Zmax(t+1)、Zmin(t+1)为t时段末水库运行的允许最高与最低水位，即非汛期正常蓄水位或汛期汛限水位与死水位，单位m，由此构造的水位约束条件为：

Zmin(t+1)≤Z(t+1)≤Zmax(t+1)

(5)

3)水位库容约条件束。设t时段初水库面积、水位和库容依次为A(t)、Z(t)、S(t)，单位为万m2、m、万m3，因此形成的库容约束函数如下：

(6)

4)供水、调度县不交叉约束。引入αi为用水户i的限制供水系数，则供水约束和调度线不交叉约束条件为：

WSi(t)≥αi×WDi(t)

(7)

Xi,j≥Xi+1,j

(8)

5)非负约束条件。根据以上各约束条件，水库供水调度各变量均为非负值。

1.5 模型求解

模拟过程中，后期收敛速度慢、前期收敛速度快为粒子群算法存在的典型特征，各粒子在种群中相差较小，并且随随着迭代次数的增大种群的多样性不断减少，由此呈现出显著的“趋同性”，这种现象加大了局部极值的发生概率，为增加种群的多样性必须此案去分群、扰动、变异等措施，算法所求的最优解即为粒子群趋同的点。

设定合理的步数阈值N作为进化停滞条件，当进化停滞步数n超过阈值时随机选取20%的粒子开始混沌变异，原聚集性粒子群利用新的运算公式驱散，由此实现增加种群多样性及解决早期收敛的问题，混沌变异算法的运算流程如图2。

2 实证分析

2.1 水库概况

大伙房水库坐落于抚顺市境内，控制面积5437km2，是一座兼顾灌溉、防洪、发电、供水、养殖等功能的大型水利工程，同时也是全国九大重点城市供水水源地之一。水库总库容21.87亿m3，防洪库容11.82亿m3，汛限水位126.4m，最高水位138.8m，最大水深37.0m，死水位108.0m，库区水面最宽达4km、东西长35km，最大蓄水面积114km2，枢纽总泄量16.295m3/s。输洞长251m，底板高程94m，洞径6.5m，一支和二支洞设置于主洞末，溢洪道设置有宽10.4m、高8.7m的5个闸门。电站总装机容量3.2万kW，年发电量5600kW·h，库区水产养殖规模大有自然“大水缸”之称，承担着辽阳、盘锦、鞍山、沈阳、抚顺、沈营口、大连等城市和2300万人口生活供水任务[9-17]。