高温复杂疲劳工况下10%Cr钢寿命特性

崔 璐， 康文泉， 吴 鹏， 罗 浩， 魏文澜， 李 臻

(西安石油大学机械工程学院， 西安 710065)

高温设备在运行时都承受着复杂循环载荷,如低周疲劳(low cycle fatigue, LCF)、高周疲劳(high cycle fatigue, HCF)以及高低周复合疲劳(combined cycle fatigue, CCF)[1-9]。作为超超临界汽轮机组的关键大型部件,例如汽轮机转子在高温运行过程中除了承受引起蠕变损伤的蒸汽压力、离心力等载荷外,还有机组启停过程中温度或大幅度负荷变化引起的低周疲劳载荷[10-11],以及由例如自重、惯性等引起的高频振动载荷[2,12-13]。几种载荷相互叠加交互会引起汽轮机转子表面开裂,机组的寿命会大幅下降。在传统的寿命设计中,通常将由温度场引起的低周疲劳损伤和由振动等因素引起的高周疲劳损伤分别考虑。虽然相对于温差引起的大幅值低周疲劳载荷,高频振动的载荷幅值很低并且可控,然而当高频振动与低周疲劳载荷交互时,材料寿命会大幅降低[1-6]。因此,对高低周复合载荷下材料疲劳损伤特性研究,可以为发挥设备零部件最大潜能或者避免设计余量不足而带来的极大不安全隐患提供理论依据。为了准确描述和预测高温部件复杂蠕变疲劳交互作用下的寿命问题,复合高频振动载荷成为继恒温低周疲劳、变温低周疲劳(thermomechanical fatigue, TMF)等研究之后的下一个热点研究方向[2]。近年来,对高低周复合疲劳载荷下的疲劳损伤研究有了很大进展,研究问题主要集中在高低周复合载荷下的疲劳性能[7,12]、高低周复合载荷下的裂纹扩展和裂纹萌生[2,14]、高周疲劳载荷下的裂纹扩展门槛值[2]、高低周复合疲劳寿命估算和微动磨损等[2-7]，以及高周疲劳载荷频率、应变幅、平均应力[15-16]和热机疲劳的温度对寿命产生的影响等方面[1]。

目前对于高低周复合载荷下材料寿命模型的研究主要是基于裂纹扩展机理模型和累积损伤模型。Schweizer等[2]、Metzger等[3]提出了一种基于裂纹扩展机理的模型,对常用于高温设备的10%Cr钢和用于内燃机气缸盖的3种铸铁材料进行了寿命预测,并与实验结果进行了对比,指出HCF与LCF的交互作用加速了裂纹扩展速率,降低了构件的疲劳寿命；因此,它可以很好地预测材料的疲劳寿命,且预测结果与实验结果吻合度较好。William等[17]提出了一种概率模型,用来预测带缺口部件的高周疲劳裂纹萌生和裂纹扩展。Norman等[18]提出了一种幂律法则模型来描述高周疲劳载荷对构件寿命的影响,此模型认为疲劳微裂纹的扩展取决于裂纹尖端张开位移水平。Stanzl-Tschegg等[19]使用叠加在LCF上的HCF进行了变幅疲劳测试,实验结果表明,叠加变幅载荷下的疲劳寿命比在定幅载荷下短得多。通过表征高周应力幅值和低周应力幅值对复合疲劳损伤的影响,Zheng等[6]发现高低周疲劳载荷的交互作用会对构件造成一种额外的损伤,为此提出了基于指数衰减定律的高低周复合疲劳交互寿命预测模型,此模型应用指数规律来近似描述疲劳交互损伤的演化,考虑了高低周疲劳载荷的交互作用,可以较好地评估这种交互作用造成的寿命失效问题。赵振华等[13]对钛合金TC11试件进行了低周、高周和高低周复合疲劳实验,提出了线性和非线性损伤累积模型。通过对比两种模型的估算结果与实验结果,发现考虑了高低周复合疲劳循环比和应力(应变)幅比的非线性模型的估算精度较好,误差分布均匀,与实验值吻合较好。章胜等[20]以Goodman直线模型构造考虑了结构应力集中和材料分散性后的最差件等寿命曲线,将循环应力等效成当量稳态应力,从而建立了相应的高低周复合疲劳寿命分析方法。石欣桐等[21]基于多机制损伤耦合模型,以LY12CZ为研究材料,建立了高低周复合疲劳金属疲劳寿命预估模型,其预测结果较为准确。郭学东等[22]对不同温度、不同应力比下沥青混合料疲劳寿命展开研究,结果表明,温度相同时,应力比的增大使沥青路面疲劳寿命变短,且裂纹扩展寿命占疲劳全寿命的百分比和温度呈指数关系。

可以看到,近几年来,对于高低周复合问题的研究是疲劳领域的重点。在当前的疲劳寿命预测方法中,对由HCF/LCF交替变化导致的交互作用引起的损伤考虑较少,且对于应变比与寿命间的关系研究较少。由于载荷间相互作用会对复合疲劳寿命产生重大影响,在此基础上,以超超临界火力发电厂汽轮机用新型马氏体转子钢的典型代表10Cr-1Mo-1V(10%Cr钢)为研究对象,分别通过实验分析高周、低周和高低周复合疲劳特性,提出了一种高低周复合疲劳寿命预测模型,考虑了交互作用对高低周复合疲劳寿命的影响。

1 实验材料及方案

实验包括低周疲劳实验、高周疲劳实验及高低周复合疲劳实验。其中,低周疲劳实验用于分析低周疲劳分量对疲劳寿命产生的影响,高周疲劳实验用于分析高周疲劳分量对疲劳寿命产生的影响,材料在高低周复合疲劳载荷下的实验用于分析高低周复合疲劳交互作用对寿命产生的影响。

1.1 实验材料

材料选用9%～12%Cr现代铁素体-马氏体耐热钢的典型代表10%Cr钢,由欧盟COST项目研发,主要应用于服役工况高达600 ℃/300 bar(1 bar=100 kPa)的先进汽轮机转子。其化学成分和力学性能分别如表1和表2所示,热处理工艺为奥氏体化1 050 ℃/7 h/油冷+570 ℃/10.25 h/空冷+690 ℃/10 h/炉冷。

表2 10%Cr钢的力学性能Table 2 Mechanical properties of 10%Cr

1.2 实验方案

实验主要分为三大类型:高温低周疲劳实验、高温高周疲劳实验以及高温高低周复合疲劳实验。低周疲劳实验和高低周疲劳实验采用应变控制形式,低周疲劳实验温度分别为600、550、500、450、300 ℃,高低周复合疲劳实验温度分别为600、550、400 ℃。高周疲劳实验采用应力控制形式,分别在300 ℃和600 ℃下进行。载荷谱采用正弦波型,频率为40 Hz。实验进行到试样断裂时结束,断裂时的循环数为试样疲劳寿命。采用螺纹连接型圆棒形试样,实验的过程依据ISO12106[23]标准完成。

2 实验结果与分析

2.1 低周疲劳实验

图1所示为不同温度下的低周疲劳寿命曲线,可以看出,在相同的温度下,试样的疲劳寿命随应变幅的增大而降低。在相同的应变幅下,疲劳寿命随温度的升高而降低,且当温度超过500 ℃时,疲劳寿命降幅较快,如果机械载荷加载过程中也伴随有温度的交变,其寿命会比最恶劣工况(最高温度工况)大幅度降低。

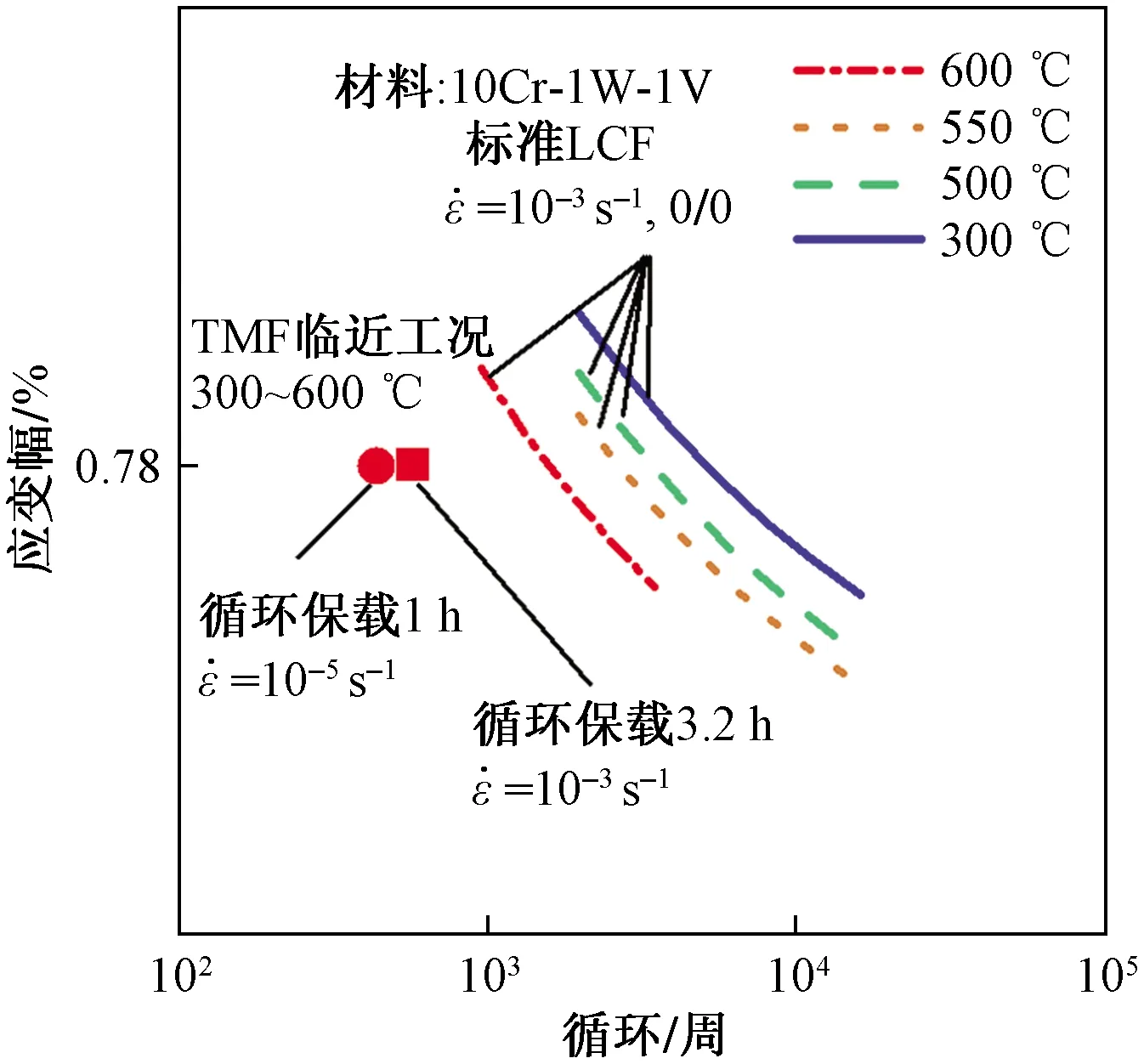
图1 不同温度下的低周疲劳寿命曲线Fig.1 LCF life at different temperatures

2.2 高周疲劳实验

高周疲劳实验分别在300 ℃和600 ℃下进行,该温度是先进汽轮机组的冷启动温度和稳定运行温度。实验结果如图2所示,高周疲劳循环数随载荷应力幅的增大而减小,随温度的增高而降低。图2中箭头表示实验正在进行中,带有台阶型箭头表示实验进行到一定循环后还未出现裂纹,载荷提升10%后继续进行。另外,开展高温高频疲劳实验,除了可以表征热力设备材料的高周疲劳特性,还可以用于图1中所示的辅助低周疲劳特性曲线向低载荷区域外推研究[24]。

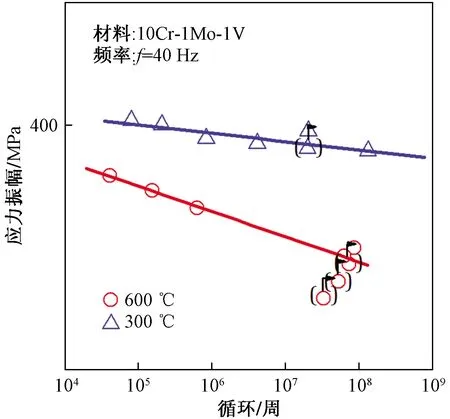
图2 不同温度下的高周疲劳寿命曲线Fig.2 HCF life at different temperatures

图3所示为叠加50 Hz频率高频振动载荷的高低周复合疲劳寿命特征曲线[2],其中纵坐标表示的为载荷谱中低周应变幅。在完全相同的高低周复合载荷谱下,疲劳寿命随温度的升高而降低。如果所叠加的高频振幅的载荷相同,疲劳寿命随着低周振幅的升高而增大[图3(a)]。相对于纯低周疲劳,即使所叠加的高频振动振幅很小,疲劳寿命也会大幅缩短,且寿命缩短可高达100倍[图3(b)]。两种情况下的复合疲劳寿命都小于相应的纯高周、纯低周疲劳振幅时的低周疲劳寿命。与此同时,如果在相同的低周振幅下,疲劳寿命随所叠加的高频振幅的增大而缩短。由此可见,在低周载荷上所叠加的高频振幅与低周应变幅之比,即相对应变幅ΔεHCF/ΔεLCF,与相应低周疲劳寿命的缩短量成反比关系。

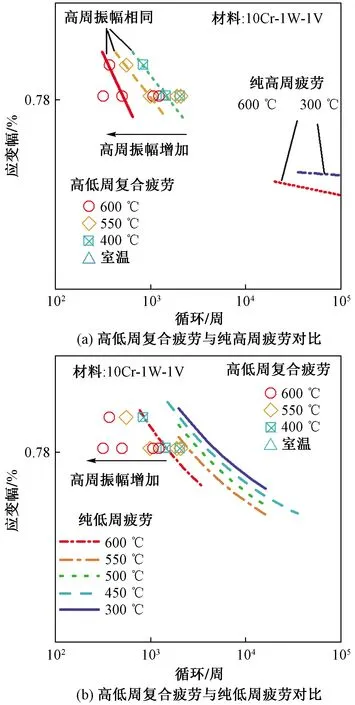
图3 高低周复合疲劳与高周、低周疲劳对比Fig.3 Comparison of CCF with HCF and LCF

2.3 高低周复合疲劳及其寿命模型

相较于大幅值高温低周疲劳载荷,高频振动的载荷幅值相对较低且可控,因此一般在先进机组高温部件寿命设计和可靠性评估中,通常以加大安全系数的方法估算高频振动引起的部件损伤。然而,高频振动与热机疲劳、低周疲劳等复合交互作用不容忽视,且机组的寿命会因此大幅下降。考虑到叠加的高周疲劳载荷会降低材料的疲劳寿命,即高低周复合疲劳寿命小于纯低周载荷下的寿命,则这两种工况下的寿命比NHCF/LCF/NLCF∈(0,1)。另外,由于所叠加高频振动的频率对其复合寿命的影响可以忽略[1],因此高周频率也不会影响到复合寿命与低周寿命之间的比值(NHCF/LCF/NLCF),而高周疲劳应变幅大小是决定高低周复合疲劳寿命减少程度的重要因素,为此做了600 ℃下应变幅比(ΔεHCF/ΔεLCF)-寿命比(NHCF/LCF/NLCF)曲线[2],如图4所示。在双对数坐标下,其规律如散点图所示,对其进行非线性拟合后,发现两者呈幂函数关系[y=a(1-x-b),a=-1.039 58,b=-0.119 75],拟合相似度为0.977 7。此外,500、400 ℃、室温下的实验所得结果,均集中在600 ℃数据拟合曲线附近。

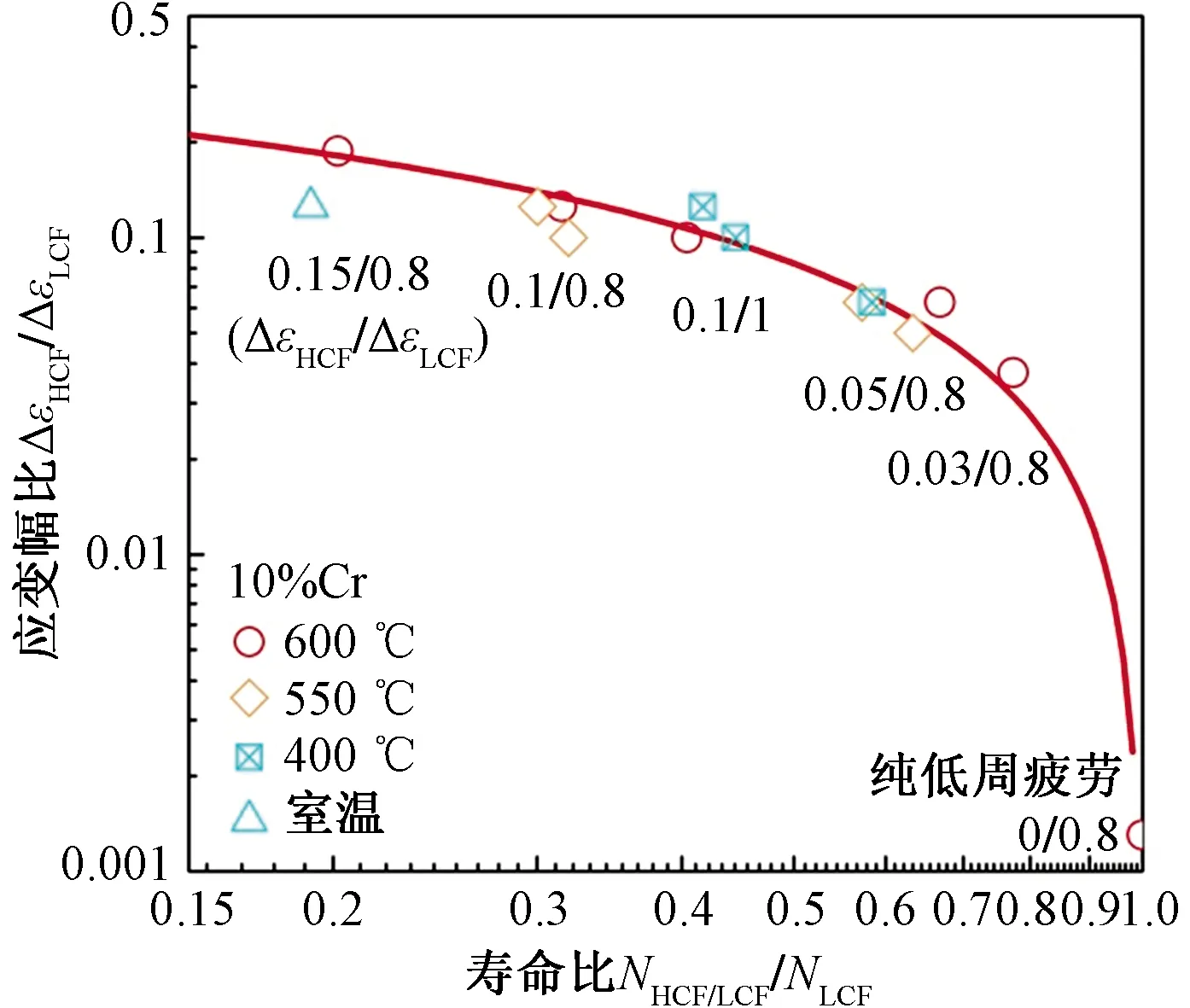
图4 高低周复合疲劳实验下的应变幅比-寿命比曲线Fig.4 Strain amplitude ratio-life ratio under CCF experiment

根据应变幅比与寿命比有：

(1)

式(1)中：NHCF/LCF为高低周复合疲劳寿命，周；NLCF为低周疲劳寿命,周,可由高低周复合疲劳实验对应的低周疲劳实验求得；ΔεLCF和ΔεHCF分别为施加在高低周复合疲劳载荷谱上的低周、高周疲劳载荷应变幅,%；a、b与材料及工况有关。

从图4中可以看出,在相同的低周疲劳载荷振幅下,叠加的高周疲劳载荷振幅越大,材料的寿命越短(ΔεHCF/ΔεLCF=0.15/0.8时的寿命小于ΔεHCF/ΔεLCF=0.1/0.8时的寿命)。同样,高周疲劳载荷振幅相同时,低周疲劳振幅越小,疲劳寿命越小(ΔεHCF/ΔεLCF= 0.1/0.8时的寿命小于ΔεHCF/ΔεLCF=0.1/1时的寿命)。即高周振幅占的相对比例越大,疲劳寿命减小的幅度越大；比值ΔεHCF/ΔεLCF越小,寿命越长。当高周振幅达到或超过门槛值时,随高周振幅的增大,疲劳寿命降低[1]。将此规律延伸，即高周振幅与低周振幅应变幅比ΔεHCF/ΔεLCF存在门槛值,达到或超过该门槛值,才使得高低周复合疲劳寿命大幅度减小。

利用以上的分析模型可以对高低周复合疲劳寿命进行初步估算,借助此方法,可以直接根据高低周复合疲劳应变幅的比值和寿命之间的关系对复合疲劳寿命进行预测。这种直接通过实验条件求出材料疲劳寿命的方法计算简便、方法直接,同时高周疲劳与低周疲劳的应变幅比(ΔεHCF/ΔεLCF)反映了高低周疲劳的交互作用。

由于材料和工况不同,计算式中系数a、b呈现差异。拟合相似度越高,a、b越小,精度越高。将式(1)转化为式(2)的形式,即可求得高低周复合疲劳寿命。当低周疲劳应变幅恒定时,对应的纯低周疲劳寿命NLCF为固定值；此时,随高周疲劳应变幅的增大,高低周复合疲劳寿命NHCF/LCF减小。当低周应变幅恒定时,高周应变幅发生变化,拟合相似度较高；同样,高周应变幅恒定,低周应变幅发生变化,拟合相似度较高。说明高周疲劳、低周疲劳应变幅交替发生变化时,拟合精度更高,而自变量以此形式发生变化正好符合实际工况。

(2)

3 结论

(1)温度恒定,加载不同应变幅值时,试样的低周疲劳寿命随应变幅值的增大而减小；应变幅恒定时,温度越高,试样的低周疲劳寿命越小。同样,高周疲劳寿命随应力幅的增大而减小,随温度的升高而减小。

(2)在相同的低周疲劳载荷振幅下,叠加的高周疲劳载荷振幅越大,材料的复合疲劳寿命越短；高周疲劳载荷振幅相同时,低周疲劳振幅越小,复合疲劳寿命越短；高周振幅占的相对比例越大,复合疲劳寿命减小的幅度越大；应变幅比(ΔεHCF/ΔεLCF)越小,相应的寿命越长。

(3)在双对数坐标中,高低周复合疲劳载荷下,应变幅比(ΔεHCF/ΔεLCF)与寿命比(NHCF/LCF/NLCF)两者呈幂函数关系[y=a(1-x-b)],高低周复合疲劳寿命模型通过高周疲劳和低周疲劳应变幅的交替变化来反映高低周复合疲劳交互作用,进而对寿命产生影响。通过应用此模型,可由已知点推测其他应变幅值下的寿命比,将曲线进行延伸,从而获得整个寿命区间的数据。