熵权-集对分析模型在列车走行性综合评估中的应用
2020-08-03卢永飞陈志敏余云燕
卢永飞,陈志敏,余云燕
(1.西北民族大学 土木工程学院,甘肃 兰州,730030;2.兰州交通大学 土木工程学院,甘肃 兰州,730070)
随着列车行驶速度的不断提高和列车载荷的不断加大,列车通过桥梁的安全性和平稳性问题越来越得到人们的重视.然而由于列车过桥时列车-轨道-桥梁的动力相互作用是一个非常复杂的过程,许多相关因素都具有一定的随机性和模糊性,以致使实测数据不可避免的产生随机误差,对列车运行安全性和平稳性最终评价结果产生一定的影响[1-4].针对该情况采用模糊诊断方法评估该动力相互作用系统的安全性和平稳性是行之有效的.2000年,翟婉明等[5]首次从车辆-轨道相互作用整体系统的角度,运用车辆-轨道耦合动力学理论,对列车走行性受轨道结构刚度的影响规律进行了研究.2002年,曾庆元院士[6]第一次提出了列车脱轨能量随机分析理论,用此理论预报了一货物列车脱轨实例,预报结果与实际脱轨事故分析结果基本一致,并计算了该试验列车最大振动响应,计算结果与测试结果良好接近.在文献[6]的基础上,2002年,向俊等[7]进一步论述了列车脱轨能量随机分析的理论与实践,再次作了实例脱轨分析,提出了预防列车脱轨的措施,得到车轨系统抗脱轨安全系数的计算方法.2011年,周智辉等[8]人运用列车脱轨能量随机分析理论分析了金温线武义江桥列车走行性,并基于该理论,对铁路桥梁行车安全指标分析方法进行了研究.2015年,梁世庆等[9]把物元可拓数学方法、熵权理论和关联度函数运用到轨道交通建设中,建立了轨道交通建设时序决策的熵权物元可拓模型.2018年,刘清漪等[10]将交通、经济、社会和环境作为轨道交通的影响子系统,设计量化模型计算了外部效应对轨道交通线路的影响程度,并对深圳地铁3号线建立灰色聚类模型进行了实例分析.KUMAR K和GORTMAKER S L等人已经将集对分析理论已经广泛应用于多个领域[11-15].借助于指标数据测定的确定性和不确定性分析,本文运用集对分析理论,先对所测列车运行指标进行定性分析,通过计算联系度对列车过桥运行安全性和平稳性做出定量分析,在确定所测列车运行指标权重时,运用数学中的信息熵反映实测数据的效用值,对列车过桥运行安全性和平稳性做出全面、客观的评价,最后通过一实例应用对铁路桥上列车的走行安全性和平稳性做出评估.
1 熵权-集对分析模型
1.1 集对分析原理
集对概念由我国学者赵克勤提出,用来处理不确定性问题的一种数学分析方法.集对分析理论的核心思想:在具体问题背景下,对集合A、B组成的集对进行分析,两组集对得到N个特性,其中有S个为集对A、B所共同具有的元素数,有P个 为A、B中相互对立的元素数,在其余F个特性关系为既不共有也不对立[16],则两个集合的联系度
(1)
其中,(a+b+c=1).式中:μ为集合A、B的联系度;S/N、F/N、P/N分别为集合A与集合B的同一度、差异度、对立度,分别简记为a、b、c;i为差异标记,在[-1,1]区间视不同情况取值;j为对立系数,一般取为-1,也可仅起标记作用.联系度μ与不确定系数i是本理论的核心,该理论对常见的一系列不确定现象均能够进行描述.
1.2 列车过桥走行性评价的集对分析方法
基于集对分析的列车过桥运行安全性和平稳性评价是将列车过桥走行性实测数据与规范或标准中的列车过桥走行性评价指标构成一个集对,分析构成的两个集对,就可以得到安全性和平稳性评价的量化指标.列车过桥运行安全性和平稳性评价常规评价指标有7个,分别为脱轨系数、轮重减载率、轮轨横向力、车体垂向加速度、车体横向加速度、Sperling舒适性垂向指标、Sperling舒适性横向指标,设一组实测样本中优于标准的有S个评价指标,劣于标准的有P个评价指标,未测或缺乏比较的有其余的F个评价指标构成,则各数据样本的联系度可通过式(1)计算出,公式中a、b、c三个数据的大小关系可初步反映该组样本数据所得评价指标的优劣.
列车过桥安全性和平稳性评价指标特性属于越小越优型,其联系度为
(2)
式中S1、S2、S3分别为标准的界限值;t为第t项指标;s为第s个待测样本;x为测点s的第t项评价指标的实测值.
1.3 指标权重系数
在目前已有的列车过桥运行安全性和平稳性评价中,各项评价指标均取等权重,没有考虑到不同指标的相对重要性,不能符合实际列车运行情况,使得走行性评价结果不够准确.指标权重的合理性与安全评价的准确度息息相关,在基于熵权-集对分析的列车过桥运行安全性和平稳性评价模型中,这里采用熵权法来确定各指标的权重,计算步骤如下[17].
(1)先构建m个评价对象,每个评价对象设有n个评价指标,构成判断矩阵R
R=(rst)m×n,(s=1,2,…,m;t=1,2,…,n)
(3)
(2)R归一化处理,得到矩阵B.
越大越优型指标为
越小越优型指标为
(4)
(3)各评价指标的熵为
(5)
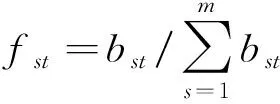
当fst=0时,lnfst无意义,可将其修正为
(6)
(4)计算各项指标的熵权
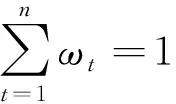
(7)
1.4 基于熵权的集对分析
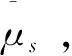
(8)
式中,n为评价指标的个数.
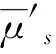
2 实例应用
以文献[1]中武广高速铁路典型桥梁动力特性和列车走行型评估报告中梁家湾特大桥的列车动力响应数据为例,在不同车速下共有6组实测数据,每一组数据样本有7项评价指标分别为脱轨系数、轮重减载率、轮轨横向力、车体垂向加速度、车体横向加速度、Sperling舒适性垂向指标、Sperling舒适性横向指标见表1.依据相关规范将列车走行性状况分为3级[18-19],Ⅰ级为优秀,Ⅱ级为良好,Ⅲ三级为合格,其中轮轨横向力指标门限值根据测试车轮静荷载计算得到,集体分级标准见表2.

表1 列车过桥走行性评价指标实测数值

表2 列车过桥走行性评价指标分级标准
首先根据式(1)以列车走行性分级Ⅰ、Ⅱ、Ⅲ的级别作为分析对象联系度表达式中的同一度、差异度、对立度的取值界限,计算6组测量样本数据的集对分析联系度分别为:
比较6个列车走行性评价样本的联系度可知:样本3、5属于同一级别,列车走行性状况从优到劣依次为1、2、6、3和5、4.为进一步分析实测指标的具体数值与列车走行性分级标准之间的数量关系,需对各测点样本数值做同一、差异、对立的进一步分析.
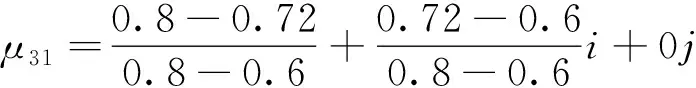
j=0+0.933i+0.067j
μ33=1+0i+0j
i+0j=0.788+0.212i+0j
μ35=1+0i+0j,
i+0j=0.08+0.92i+0j
μ37=1+0i+0j
用MATLAB对熵值法确定权重系数过程(3)-(7)式进行编程如图1,分别输入6种不同的车速对应的6组实测数值,计算得到列车过桥走行性评价指标的各自权重见表3.

图1 MATLAB流程图Fig.1 MATLAB program chart

表3 列车过桥走行性评价指标权重

表4 列车过桥走行性评价结果
各种车速下列车安全性和平稳性状况从优到劣依次为1、2、6、5、3、4.车速序号1、2、6列车过桥车速最小,所得列车安全性和平稳性状况最优,样本4列车过桥车速最大,其安全性和平稳性最差,整个评价结果与实际相符.
3 结论
(1)本文应用数学上的集对分析理论构造列车走行性评价模型,在确定列车过桥运行安全性和平稳性评价的7个常规评价指标权重时引入了信息论中熵值理论,通过信息熵理论计算列车过桥运行实测数据本身的效用值来确定各个指标的权重,使得指标权重的分配有理可依.
(2)与常规列车过桥运行安全性和平稳性的等权重的指标权重评价方法相比,本文的评价方法使轮轴横向力这项指标的权重增大为0.165,该结果更加符合实际情况.
(3)列车过桥运行安全性和平稳性评价是一项比较复杂的工程,需要综合多项测量指标的属性进行判定,本文仅仅考虑了列车过桥运行安全性和平稳性评价的7个常规评价指标,而且列车过桥时要受到风荷载气动影响和温度变化的动态影响,故对其进行综合评价仅仅从权重角度考虑还有待欠缺.
