复变函数法计算圆形盾构隧道周边土体位移
2020-08-03朱艳峰张雪松王和平
朱艳峰,张雪松,王和平
(1.广州番禺职业技术学院 建筑工程学院,广东 广州 511483;2.广东工业大学 土木与交通工程学院,广东 广州 510006)
地铁的建设在大中城市越来越普遍,施工过程中隧道开挖对周围环境影响很大.目前,主要有3种方法计算圆形盾构隧道周围土体的变形:经验法、理论计算和数值模拟.而在理论计算方面主要有双击坐标法、镜像法、复变函数法和Airy应力函数法.
复变函数求解隧道问题的优点为,能够把半无限空间映射为定值圆环,而不会影响解析函数求解,并且无穷远端也被映射到圆弧上一点,通过位移差,可以保证无穷远端位移为零.Verruijtt[1-2]应用复变函数分别推导出了隧道孔洞周围在均布径向位移和应力条件下的解析解.王立忠[3]、童磊[4]、张治国[5]均利用Park[6]或相似的经验边界椭圆化变形形式完成了隧道土体变形复变函数求解.由于经验边界变形形式的引入,使得解析解变得有针对性.
本文在前人研究基础上,利用隧道边界土体和位移协调关系及混凝土衬砌相对空间位置,建立位移函数关系,进一步求出圆形盾构隧道周围土体变形复变函数解,最后采用Matlab软件实现算法.
1 隧道位移函数
1.1 基本假设
为了满足平面应变要求,假定隧道在轴线上无限长;土体为半无限空间弹性体;土体和衬砌相互作用,满足协调变形条件,但二者之间无摩擦力[7];不考虑渗流对变形的影响,假设盾构过程中不排水.半空间单圆孔隧道平面简图如图1所示,采用复数直角坐标系表示,h为隧道中心埋置深度,r0为隧道半径,A为坐标原点,B为无穷远端,C为隧道顶,D为隧道底,R区域为隧道孔洞外区域.
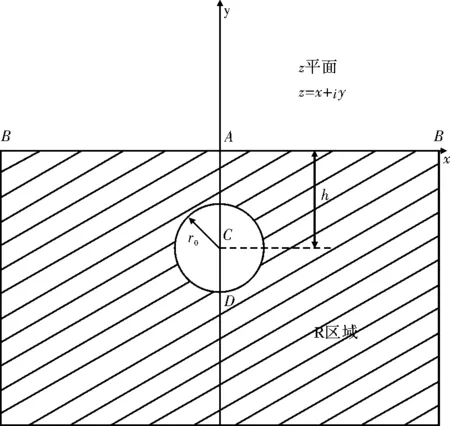
图1 单孔半无限空间Fig.1 The half plane with a circular cavity
1.2 位移函数
根据Muskhelishvili[8]平面问题复变函数解法,可以用R区域内的解析函数φ(z)和ψ(z)来表示土体应力和位移分量.应力公式如下
(1)
(2)
位移公式如下:
(3)
(4)
(5)
式中,G为土体剪切模量,G=E/2(1+υ),E为土体弹性模量,υ为土体泊松比;Ux为土体水平位移,Uy为土体竖向位移;参数κ=3-4υ.


(6)
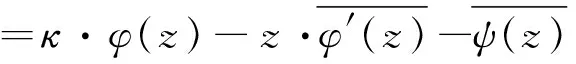
(7)
2 复变函数理论
2.1 共形映射
通过Mobius共形映射公式变换,z平面半无限空间中单孔圆形隧道可以转换为ζ平面中定直径圆环,图2为映射后区域.共形映射表达式为
(8)



图2 Mobius共形映射区域Fig.2 Plane of Mobius conformal transformation
2.2 Laurent级数展开
φ(z)和ψ(z)在R区域内是解析函数,根据复变函数理论中解析函数定理,φ(ζ)和ψ(ζ)在r区域内也是解析函数.φ(ζ)和ψ(ζ)的Laurent双边幂级数展开形式为

(9)

(10)
式中,a0,ak,bk,c0,ck,dk可由后文位移函数确定.
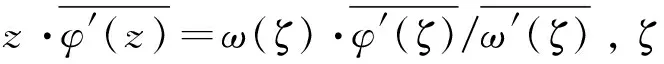
(11)
2.3 确定级数系数
地表应力边界条件,即式(6)改写为
(12)
将式(9)~(11)带入上面式(12),得到
(13)
k=1,2,3…
(14)
k=1,2,3…
(15)
隧道洞口位移边界条件,即式(7)改写为

(16)
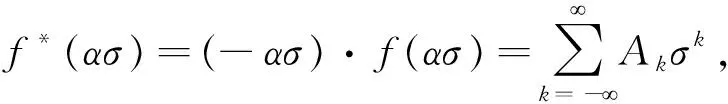
k=1,2,3…
(17)
k=1,2,3…
(18)

(19)

(20)
3 隧道土体变形复变函数解
3.1 隧道土体变形计算模型
盾构隧道开挖面与衬砌之间存在间隙,为反映隧道开挖推进过程和隧道施工造成的地层损失,Lee[9]提出了间隙参数g,其表达式为
(21)

Loganathan[10]等研究发现,圆形隧道地层变形呈椭圆化变形,由此得出地层损失率经验公式;Sagaseta[11]提出隧道边界最终变形由造成地层损失的洞口径向均匀收缩、隧道面竖向沉降以及不引起体积变化的衬砌椭圆化变形组成;Park[6]根据工程经验提出的BC-3和BC-4椭圆化边界变形形式较符合实际;王立忠[3]、童磊[4]、张治国[5]等采用Park[6]或相似的经验变形形式作为边界条件来推导解析解,在一定程度上小弱了解析解的优势.
本文根据混凝土衬砌与隧道孔洞土体相对位置以及位移协调关系,建立函数关系,完成求解.
衬砌与隧道孔洞空间位置如图3所示,实线表示未变形前衬砌和孔洞空间位置,虚线所示的椭圆形为变形后土体与衬砌边界线.
二者位移关系采用极坐标表示为
(21)

图3 隧道土体变形计算模型Fig.3 Deformation modes of tunnel cavity
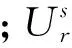
根据Flüegge[12]衬砌位移 - 应力关系(满足假设衬砌厚度远小于隧道半径),得
(22)
(23)
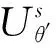
(24)
(25)
式中:Es为衬砌的弹性模量;νs为砌体的泊松比;As为每延米衬砌圆环的截面面积;Is为每延米
衬砌圆环对圆心的惯性矩.
根据土体与衬砌之间无摩擦的假定可知二者接触面上的应力关系为
(26)
(27)

当r=r0时,由式(21)~(23)、(26)和式(27)可得

(28)
求解式(28)微分方程并取特解
(29)
式中,σr为衬砌与土体接触面上衬砌对土体的 应力,浅埋隧道σr=γ(h-r0sinθ′),γ为土体重度,令m=1+F/C和n=Fr0(1-ν2)/E,最终得
Ur|r=r0=m[-u0(1+sinθ′)]+nγ(h-r0sinθ′)
(30)
3.2 复变函数解
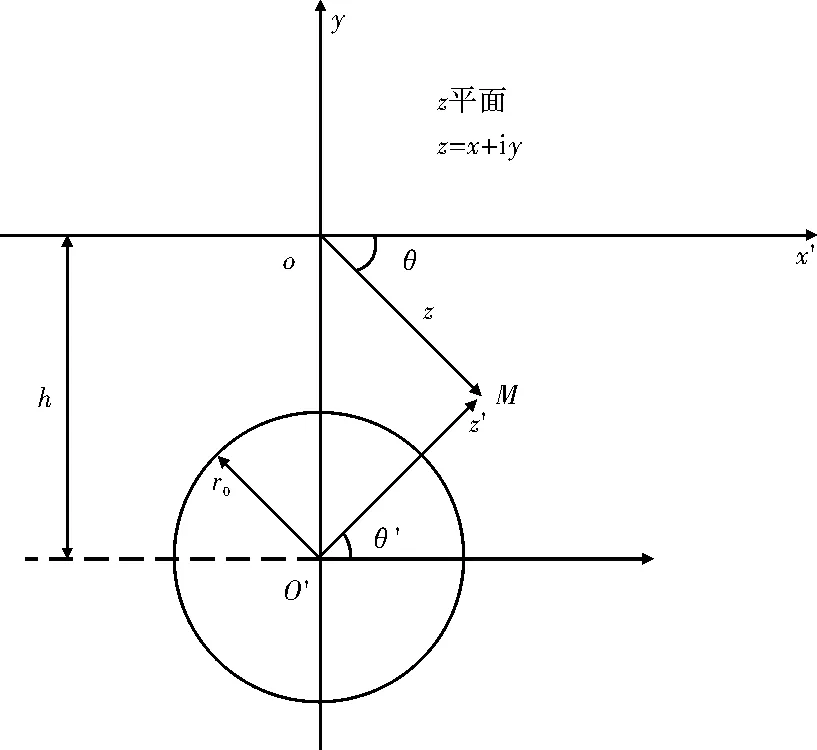
图4 极坐标转换Fig.4 Transformation of polarcoordinate
因为上述x′o′y坐标系与复变函数建立的xoy坐标系不同所以对隧道周边的位移条件变换成如图4所示的形式.二者之间的关系为
z=z′-ih
(31)

(32)
(33)
由式(31)~(33)可得到
(34)
(35)
将式(30)转化到z平面上,得到
(36)
将式(36)转化到ζ平面上,得到

(37)
将式(37)代入式(16),得到
f*(ασ)=(-ασ)·f(ασ)=2(1-ασ)Gu|ρ=α
(38)
则上面各系数为
A0=-(1+α)2mGu0i
(39a)
A1=(2+3α-α3)mGu0i+(2α-α3-1/α)nr0γGi
(39b)
Ak=-(1-α2)2αk-2(mu0-nr0γ)Gi
(39c)
A-k=0
(39d)
3.3 算法实现程序
本文采用Matlab软件实现解析函数求解过程,最终完成隧道周围土体变形计算.编制的运算程序包括9个参数,分别为隧道埋置深度、隧道半径、衬砌内半径、空隙参数、土体弹性模量、土体泊松比、衬砌弹性模量、衬砌泊松比和土体重度[13].
(1)假定初始a0为任意某一虚数,带入公式,求得ak,bk;

(3)将a0、ak、bk带入公式,求得ck,dk,即求出解析函数φ(ζ)和ψ(ζ),根据z与ζ关系,确定解析函数φ(z)和ψ(z);
(4)根据位移公式,确定其实部和虚部数值,即为土体的水平位移和竖向位移(在计算时需注意,各点位移需减去无穷远处位移,才与无穷远端位移为零的设定相符合).
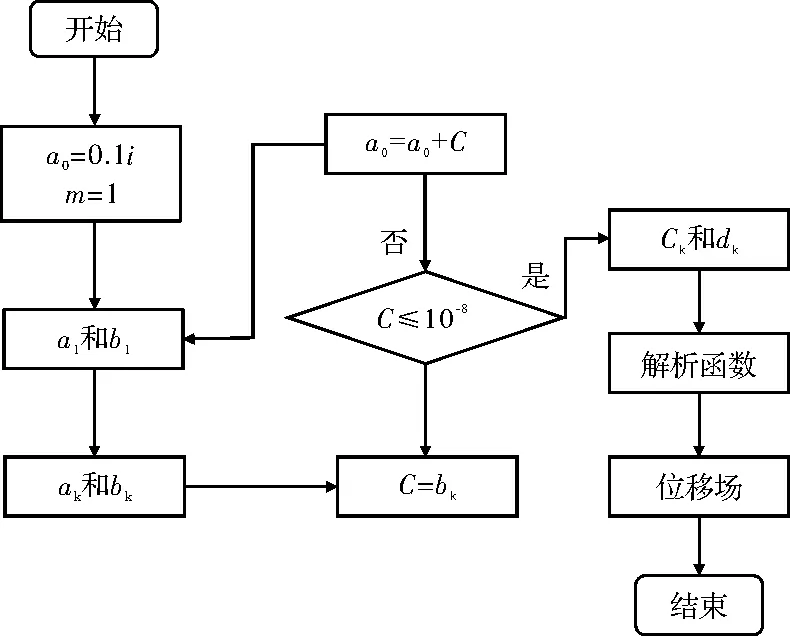
图5 程序流程图Fig.5 Flow chart of program
4 计算结果分析
4.1 计算结果与实测数据对比
应用Matlab复变函数解程序计算Loganathan[10]文章中的Heathrow隧道、Thunder Bay隧道、Green Park隧道、Barcelona隧道和Bangkok下水道地表沉降量,并将计算结果与各隧道实测地表沉降量对比.5条隧道的工程参数如表3所示,其它参数E=Eu,ν=0.2,Es=25 000 MPa,νs=0.2.

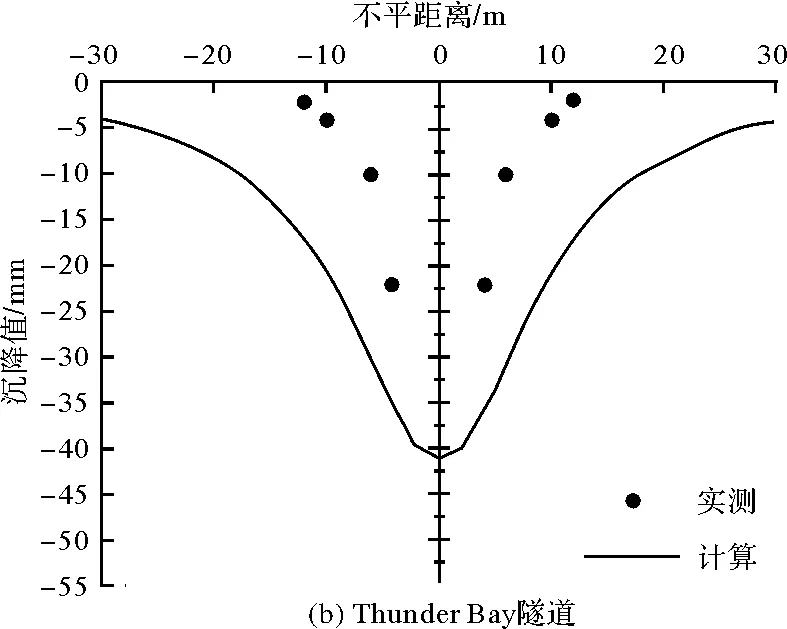
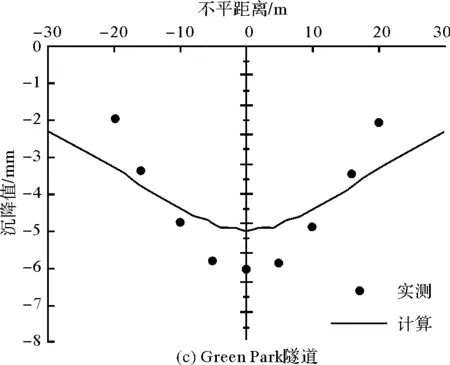
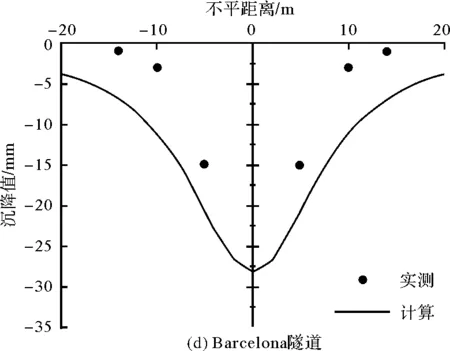

图6 各隧道地表沉降量对比Fig.6 Comparison of ground surface settlements of tunnels
隧道地表沉降量理论计算值与实测数据对比结果如图6所示,x轴和y轴分别表示地表水平距离(m)和沉降值(mm).从图中可以看出,采用本文复变函数方法计算所得沉降量曲线与实测数据分布一致,符合Peck正态曲线特征.在隧道中心线附近沉降量最大,随着水平距离增大,沉降量快速减小.同时发现,理论沉降量和实测沉降量存在一定偏差,理论沉槽宽度比实测宽度略大,需要进一步研究.
4.2 隧道地表沉降量影响因素分析
在应用复变函数求解隧道周围土体变形理论中,涉及到较多参数,而每个参数对最终结果的影响程度需要进行对比研究,在今后的隧道设计中重视这些参数的选取.通过理论公式对理论公式研究,土体弹性模量、衬砌弹性模量、衬砌泊松比等参数对土体变形影响较小.因此,本文假定了7种情况,后6种情况相较第1种情况分别改变一个参数数值,如表2所示.形成3组对比,分别就隧道埋置深度、隧道半径、土体泊松比和土体模量对地表沉降量的影响程度进行讨论.Es=25 000 MPa,νs=0.2.计算结果如图7所示.

表1 隧道工程参数
隧道埋置深度:在土质等其它参数相同情况下,隧道埋置深度越小,沉降曲线越陡,地表沉降量越大,沉槽宽度越窄.在隧道中心线附近,地表沉降量受隧道埋置深度影响较大,而远端则影响不明显.埋深减小1/4,中心沉降量增大近0.4倍,可见隧道埋置深度是隧道周围土体变形重要影响因素之一.
隧道半径:在土质其它参数相同情况下,隧道半径越大,沉降曲线越陡,但没有隧道埋置深度影响大,地表沉降量越大,沉槽宽度越大.在隧道中心线附近,地表沉降量受隧道半径影响较大,而远端影响较小.隧道半径增大1/8,中心沉降量增大近1/7,可见隧道半径是隧道周围土体变形的重要影响因素之一,但对沉降曲线形状影响一般.
土体泊松比:在隧道几何等参数相同情况下,土体泊松比越小,地表沉降量越大,沉槽宽度越大.在隧道中心线附近,地表沉积量受土体泊松比影响较大,而远端影响较小.土体泊松比减小1/5,中心沉积量增大近1/5,可见土体泊松比也是隧道周围土体变形的重要影响因素之一,但对沉降曲线形状影响较小.
上述参数对土体位移的影响,也一定程度的解释了上节中计算结果与实测结果存在偏差的现象.实际工程中,地层中土层分布复杂,与半无限空间弹性体的理想假设不同.不同层土质模量不同,而根据巴克洛夫斯基当层理论,上层模量大的土层被下层模量小的土层替换,则土层厚度增加,则影响隧道埋置深度,影响理论值大小.

表2 7种工况隧道工程参数



图7 不同工况地表沉降对比Fig.7 Comparison of ground surface settlements of different cases
5 结论
(1)本文结合衬砌和土体之间位置及变形协调关系,提出了圆形盾构隧道土体变形的复变函数解法.在本方法中,衬砌和土体径向位移差等于二者前位置差,由此推导边界变形函数,而不是采用经验边界变形函数,更具有普遍性.在计算中考虑到了无穷远端变形为零的情况,使计算结果更符合实际.
(2)本文的计算方法中涉及的参数较少,且容易测定,具有较强的通用性.
(3)随着隧道埋置深度的减小,隧道中心附近土体变形增大显著,而远端略有减小,沉槽宽度明显变窄;随着隧道半径的增大,隧道中心附近土体变形增大显著,沉槽宽度变宽;随着土体泊松比变小,隧道中心附近土体沉降增大,沉槽宽度变宽.即隧道埋置深度、隧道半径、土体泊松比均是隧道土体变形重要影响因素,而土体模量、衬砌模量等因素,在本计算方法中对结果影响较小.
