纯压弯受力下大断面盾构隧道管片接头抗弯足尺试验研究
2020-08-01方若全徐培凯
张 力,苏 芮,何 川,封 坤,*,方若全,徐培凯
(1.西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031;2.西南交通大学土木工程学院,四川 成都 610031)
0 引言
管片接头一般由管片、连接螺栓和密封垫等组成,构造复杂,是装配式衬砌结构的薄弱部分,其力学性能对于管片结构具有较大的影响[1-5]。同时由于接头处存在张开变形和螺栓受力等复杂力学关系,其力学性能参数(如抗弯刚度等)无法通过现有理论准确计算。由于计算参数的多样性和复杂性,单纯依靠数值模拟很难实现对管片接头受力和变形的精确计算。因此,为研究管片接头在压弯荷载作用下的复杂力学行为,有必要开展接头抗弯试验。
接头抗弯试验是研究接头抗弯力学行为的直接手段,与试验相关的研究较多[6-14]。其中较为典型的有:金跃郎等[10]针对直螺栓型原型管片接头开展接头抗弯试验,研究了不同轴力和弯矩作用下管片接头的竖向位移、张开变形以及抗弯刚度等参数,试验边界为一端固定铰支、一端可动铰支;柳献等[11]针对某地铁隧道管片接头,研发试验装置并开展接头抗弯试验,研究了管片接头变形、螺栓受力以及在压弯荷载下接头破坏等现象;封坤等[12]针对狮子洋隧道管片接头开展接头抗弯足尺试验,研究了不同轴力下接头张开量、抗弯刚度、混凝土应变和螺栓应变的变化规律,试验中接头试件类型为直接头,试验边界为一端固定铰支、一端可动铰支;龚琛杰等[13]通过接头抗弯足尺试验,研究了不同轴力和弯矩作用下接头变形、混凝土应变和螺栓应变与弯矩的关系;Kazuyoshi Nishikawa[14]开展接头抗弯试验,研究了管片接头竖向变形和转动变形随弯矩的变化规律。可见,接头抗弯试验中,试验边界多为一端固定铰支、另一端可动铰支,从而保证管片接头处于纯压弯受力状态,使得抗弯试验结果更加准确。在试验中实现上述边界约束时易出现以下问题:1)试验边界本身存在一定转动刚度,即不是纯铰,可能导致管片接头处受力未处于纯压弯状态;2)边界可转动幅度较小,使得接头转动变形受限,管片接头变形较大时,由于边界限制使得管片接头处的受力更为复杂,导致试验结果失真。
鉴于此,本文基于自主设计研发的盾构隧道管片结构加载试验平台,在保证试验时接头处于纯压弯受力状态的前提下,开展系列盾构隧道管片接头抗弯试验。试验中对于压弯荷载作用下接头形变以及螺栓应力等参数进行测量,并基于试验结果研究压弯荷载作用下管片接头的抗弯性能。
1 接头抗弯足尺试验
1.1 工程概况
苏通GIL综合管廊隧道工程全长5 530.5 m,其中盾构段长5 466.5 m,其纵断面如图1所示。工程起于南岸(苏州)引接站,止于北岸(南通)引接站,是世界上首次在重要输电通道中采用特高压GIL(气体绝缘金属封闭输电线路)技术。工程通过隧道穿越长江,是目前世界上电压等级最高、输送容量最大、技术水平最高的超长距离GIL创新工程。

图1 苏通GIL综合管廊隧道纵断面示意图Fig.1 Profile of Sutong GIL
隧道底面最低点标高-74.83 m,水压高达0.8 MPa,隧道顶板埋深20.4~47.8 m,含水层较厚,渗透性强。管片衬砌外径11.6 m,厚度0.55 m,采用“5+2+1”的分块方式,其中封顶块角度为16.37°,邻接块最大角度为49.09°,单侧楔形量250 mm,标准块角度为49.09°。管片分块见图2。

图2 管片分块图Fig.2 Blocking of segment
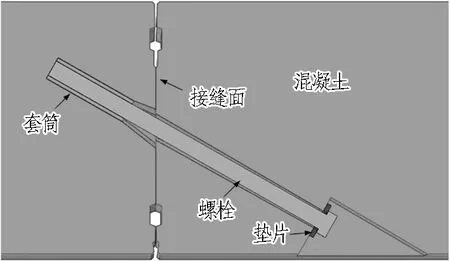
管片混凝土强度等级为C60,弹性模量为36.5×103MPa。环向接头通过3根强度等级为10.9的M36螺栓进行连接,为增强螺栓对于接缝面的约束作用,沿幅宽方向处于中间位置的螺栓插入方向与其余螺栓不同。环向接头细部构造如图3所示,连接螺栓长度为665.8 mm,其中锚固段长度为190 mm。
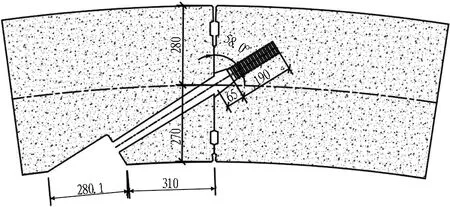
图3 环向接头细部构造(单位:mm)Fig.3 Detailed structure of segmental joint (unit:mm)
1.2 加载方式
由于试验主要研究对象为管片接头而非管片本体,因此采用更容易控制加载的“直接头”方案开展试验[13],加载方式如图4所示。这种试验方案的优点在于能较为方便、准确地控制接头处的轴力和弯矩,同时通过控制边界条件能实现接头的纯弯受力状态,使试验结果更加准确。
根据力学原理可知,试验中管片接头处弯矩的计算方法为
M=Fl+Nδ。
(1)
式中:F为竖向荷载;l为竖向荷载到支座的距离;N为水平荷载;δ为接头竖向位移。
1.3 试验装置与试件
根据图4所示的加载方式,采用接头抗弯足尺试验装置进行加载,如图5所示。其中,水平方向和竖向各有2个千斤顶,单个千斤顶的加载能力为2 500 kN,可以加载的最大轴力为5 000 kN,最大弯矩约为3 000 kN·m。试验开始后,保持水平千斤顶的荷载不变,逐步增大竖向千斤顶的力。试验中竖向荷载作用点到试件边界的距离为1.2 m。
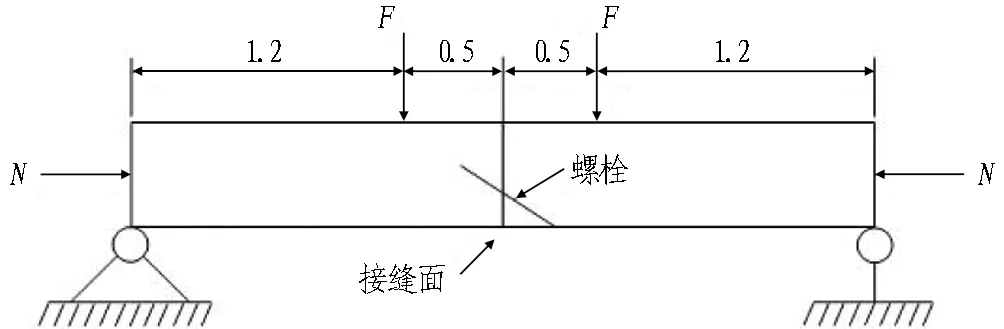
(a) 正弯加载
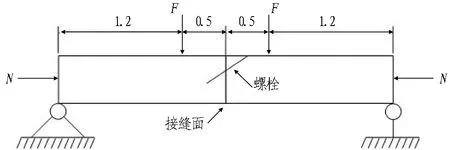
(b) 负弯加载图4 接头抗弯足尺试验加载方式(单位:m)Fig.4 Loading method of full-scale test of segmental joint (unit:m)

图5 接头抗弯足尺试验加载装置Fig.5 Loading device of full-scale test of segmental joint
原型管片的幅宽为2 000 mm,接头处通过3颗直螺栓进行连接。为了方便浇筑和开展试验,根据既有方法开展试验[12]。本次试验选取原型管片的1/3作为研究对象,即试件宽度为668 mm。根据原型管片的接头构造和配筋情况,在室内进行接头试件的浇筑和养护,试件浇筑前和浇筑后分别如图6和图7所示,待养护完成后在试验装置上进行拼装。由于接头防水材料对接头抗弯性能的影响较小[14],试验时接缝面处未放置止水条等防水材料。

图6 浇筑前试件Fig.6 Test specimen before casting

图7 浇筑后试件(单位:mm)Fig.7 Test specimen after casting (unit:mm)
1.4 边界条件
管片接头的构造复杂,导致其在承受荷载时的受力相对复杂。荷载相同而边界不同时,接头处可能出现受弯、受剪或者两者的组合,因此采用如图4所示的加载模式时,须将试件与加载装置进行连接并保证其可以自由转动,从而使接头处于纯弯受力状态。试件与加载装置的连接如图8所示,试件与铰支座通过12颗连接螺栓进行栓接(两侧各6颗),此时试件两端具有和铰支座一样的转动自由度。

(a) 试件与铰支座连接实况

(b) 连接螺栓分布情况图8 试件与加载装置连接方式Fig.8 Connection between test specimen and loading device
1.5 量测方案
在轴力和弯矩的作用下,管片接头发生张开变形和转动变形,接缝面受压侧混凝土压紧,连接螺栓因接头张开而明显受力,因此在研究接头抗弯性能时应着重分析不同轴力和弯矩下接头的张开(或闭合)变形、竖向变形和螺栓应力等参数。
1.5.1 接头变形
接头变形包括接头张开(或闭合)变形、接头竖向位移和接头张开高度。其中,接头张开量(或闭合量)和竖向位移采用测量精度为0.01 mm的差动式位移计(LVDT)进行测量,测点布置及测量方法如图9所示。接头张开高度为接头张开沿接缝面发展的高度,由于接头的竖向变形导致采用LVDT难以准确采集张开高度数据,故采用高精度钢尺沿张开高度发展方向对其进行直接测量。
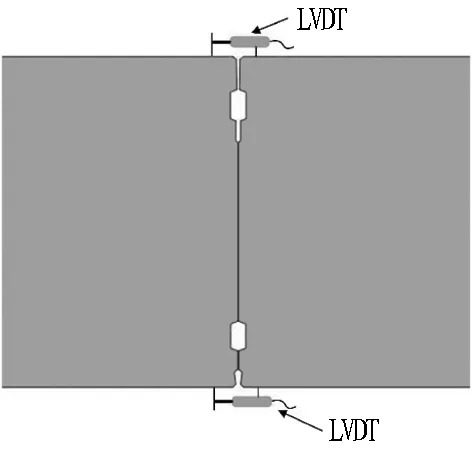
(a) 张开量和闭合量

(b) 竖向位移

(c) 差动式位移计(LVDT)图9 接头张开量、闭合量和竖向位移测量方法Fig.9 Measuring method of opening,closure and vertical displacement of segmental joint
1.5.2 螺栓应变
螺栓在管片接缝中的位置如图10(a)所示。从图10(a)中可以看出,连接螺栓与螺栓孔之间存在一定的空隙,因此在本次试验中采用螺栓两侧开槽引线连接应变片的方法,开槽宽度约4 mm,深度约2 mm(见图10(b))。应变片沿着螺栓长度方向布置,试验前在螺栓上施加95.96 kN的预紧力。
(a) 螺栓在接缝中的位置
1.6 加载工况
试验以等轴力的方式进行加载,即对于每一组轴力工况,保持水平方向荷载N不变,持续增大竖向荷载。实际工程中管片结构承受的水压最高达0.8 MPa,根据梁弹簧模型测算得到全幅宽管片结构所承受的最大轴力为12 000 kN,对应于本次试验的试件,其最大轴力为4 000 kN。鉴于此,本次试验在水平荷载1 000~4 000 kN时以1 000/3 kN为增量选取10组工况进行加载试验。每组工况下的水平荷载及其对应的最大竖向荷载如表1所示。
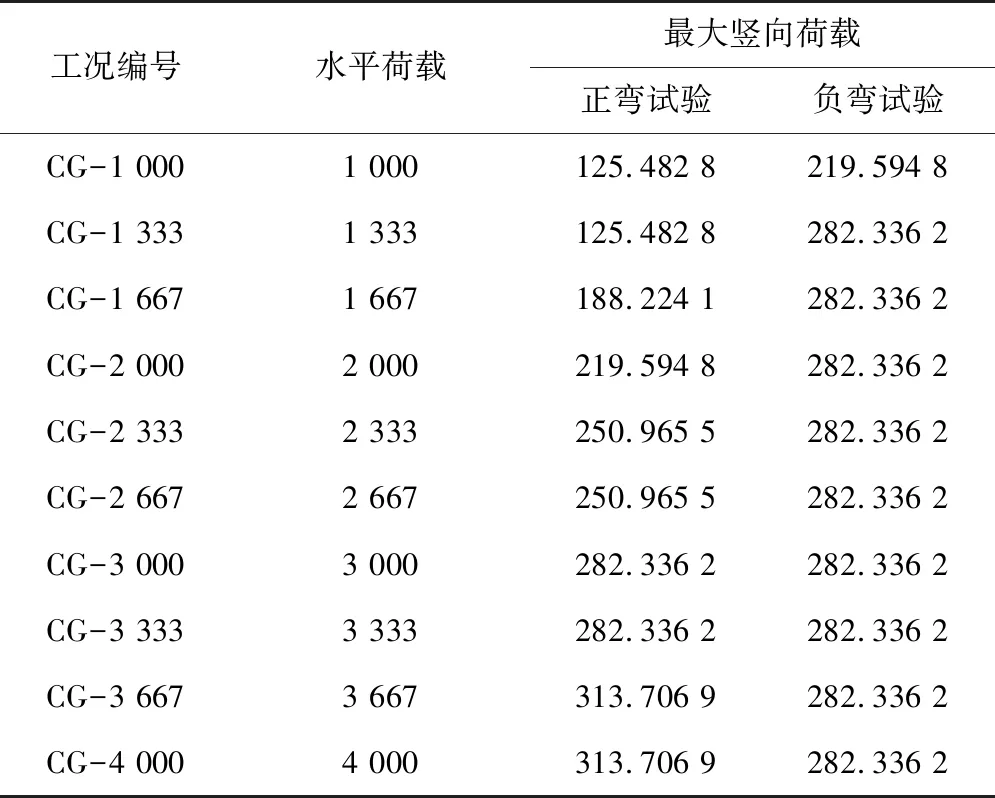
表1 接头抗弯试验加载方式工况Table 1 Loading conditions in full-scale test of segmental joint kN
2 试验结果分析
2.1 接头竖向位移
接头竖向位移随轴力和弯矩的变化规律如图11所示。由图可知:1)不同轴力下接头竖向位移随着弯矩呈非线性变化,其变化曲线可分为弯矩较小时的线性变化段和弯矩较大时的非线性变化段。2)相同弯矩作用下,轴力越大,接头竖向位移越小,表明轴力抑制接头变形,但随着轴力增大到一定程度,其抑制接头变形的效果逐渐减小。3)负弯矩下,不同轴力对应的接头竖向位移-弯矩曲线之间的间距明显小于正弯矩时曲线之间的间距,表明正弯矩下接头竖向位移对于轴力的变化更加敏感。4)轴力较小(1 000~2 333 kN)且接头竖向位移相同时,接头正弯矩略小于负弯矩;轴力较大(2 667~4 000 kN)且接头竖向位移相同时,接头正弯矩略大于负弯矩。

图11 竖向位移随着接头轴力和弯矩的变化规律Fig.11 Variation of joint vertical displacement with axial force and bending moment
2.2 接头张开量和闭合量
接头张开量和闭合量是设计接头结构和反映接头变形性能的重要参数。接头张开量和闭合量随弯矩和轴力的变化规律分别如图12和图13所示。由图12可知,正负弯矩下接头张开量随弯矩的变化规律相似,弯矩越大张开量增大的速率越大,正弯矩下接头张开量对于轴力的变化更加敏感。轴力和弯矩大小相同时,由于接头外缘的变形空间更大,正弯矩下接头张开量一般比负弯矩下接头张开量大,表明正弯矩下接头更易发生张开变形。由图13可知:接头闭合量随弯矩的变化规律存在一定差异,随着弯矩的增大,负弯矩下接头闭合量增长较快且增幅均匀,而正弯矩下接头闭合量先缓慢增大后快速增大,轴力和弯矩大小相同时,负弯矩下接头闭合量一般大于正弯矩的。

图12 张开量随着接头轴力和弯矩的变化规律Fig.12 Variation of joint opening with axial force and bending moment
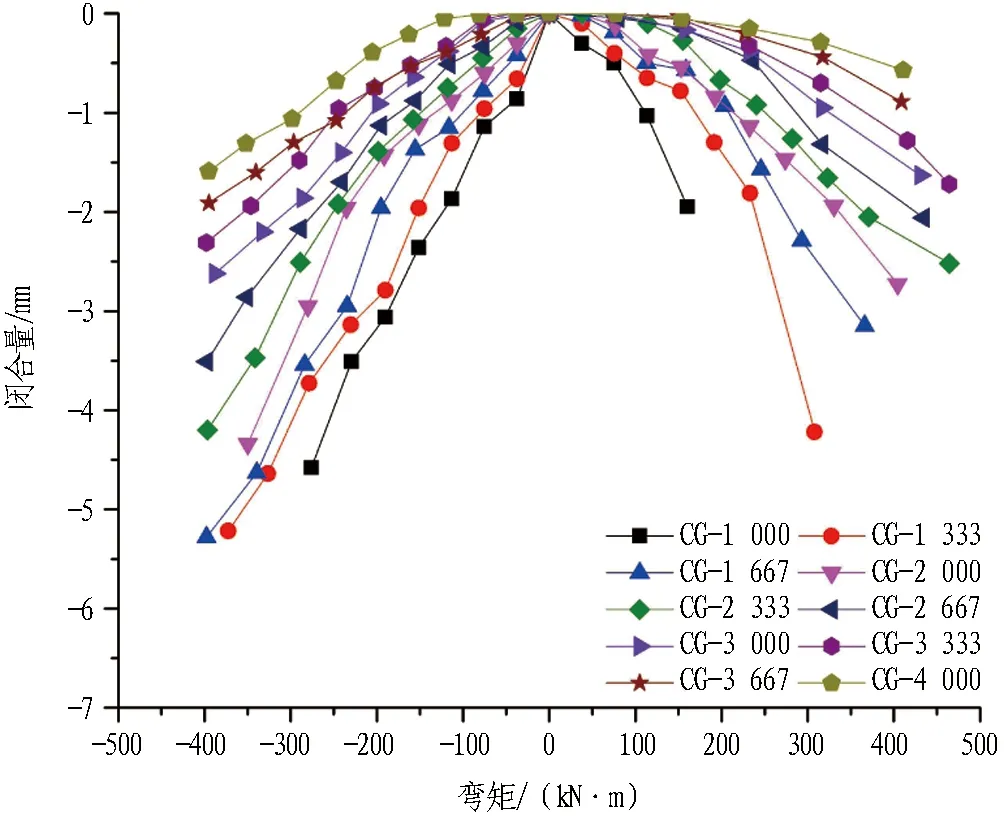
图13 闭合量随着接头轴力和弯矩的变化规律Fig.13 Variation of joint closure with axial force and bending moment
2.3 接头张开高度
接头张开高度随接头轴力和弯矩变化的规律如图14所示。由图可知,接头张开高度受弯矩作用方向的影响较大。正弯矩作用下,接头张开高度随弯矩的变化趋势为先快速增长后缓速增长,曲线在接近其最大值之前不存在明显的“平台段”;负弯矩作用下,轴力较小时(1 000~2 333 kN),接头张开高度先随弯矩增大迅速增大,而后由于螺栓的限制,张开高度随弯矩的变化曲线出现明显的“平台段”,随后随着弯矩进一步增大,接头张开高度增大速度加快;轴力较大时(2 667~4 000 kN),张开高度随着弯矩的变化曲线在出现平台段后,再随弯矩增大而增大的趋势不明显。
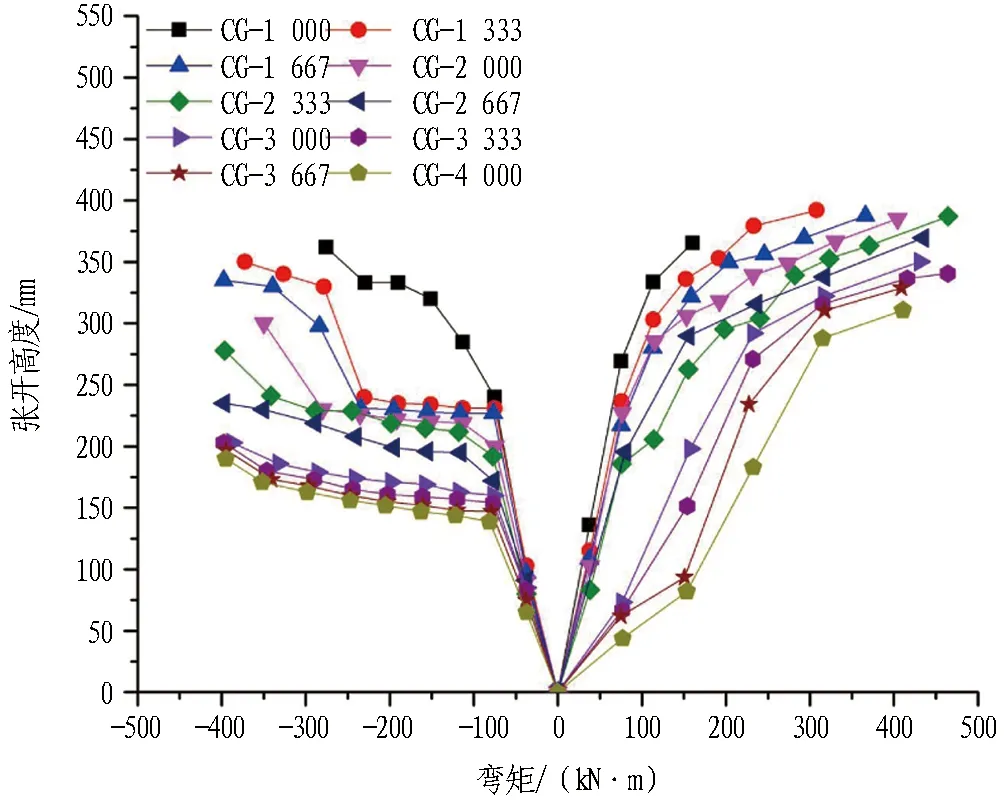
图14 接头张开高度随轴力和弯矩的变化规律Fig.14 Variation of joint opening height with axial force and bending moment
2.4 接头转动角度
接头转动角度随着轴力和弯矩的变化规律如图15所示。由图可知,接头转动角度随着弯矩和轴力的变化规律与接头竖向位移、接头张开量随轴力和弯矩的变化规律相似。接头转动角度最大值约为0.045 rad,类似接头抗弯试验中,当接头转动角度接近该值时,接头弯矩已接近破坏,而本次试验中接头转动角度接近该值时,接头处未见明显破坏现象。这可能与试验边界有关,在该边界约束下管片接头处承受荷载仅轴力和弯矩,接头可发生较大的转动变形。
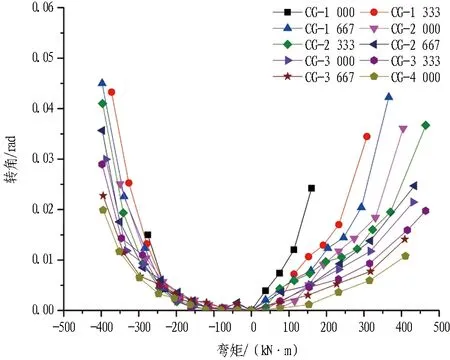
图15 接头转动角度随着接头轴力和弯矩的变化规律Fig.15 Variation of joint rotation angle with axial force and bending moment
2.5 螺栓应力
接头螺栓应力随轴力和弯矩的变化规律如图16所示。随着弯矩的增大,接头张开变形使得螺栓受拉,接头竖向变形使得螺栓受弯,图16中螺栓应力即为螺栓在拉伸和弯曲共同作用下的最大应力。由图可知,螺栓应力的最大值接近700 MPa,而螺栓的屈服应力为900 MPa,表明螺栓仍未屈服。随着轴力增大,螺栓开始明显受力时的弯矩越大;螺栓应力随弯矩增大先缓慢增大后迅速增大,其变化曲线较为平滑,表明螺栓受力仍处于弹性阶段。
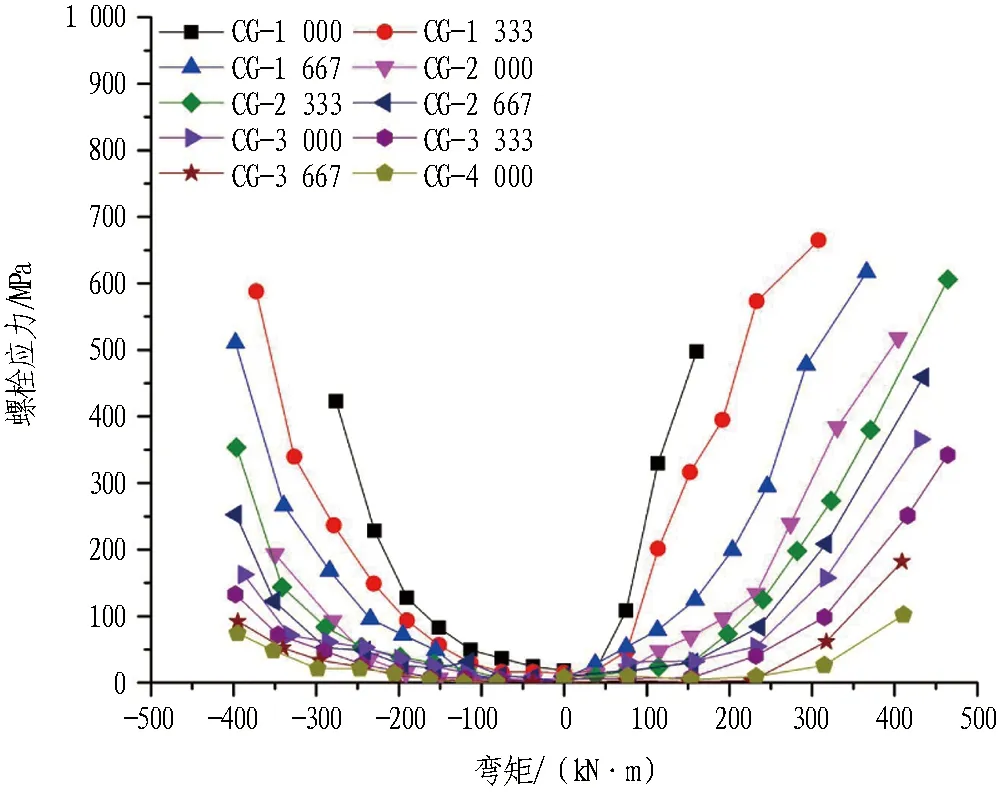
图16 螺栓应力随接头轴力和弯矩的变化规律Fig.16 Variation of bolt strain with axial force and bending moment
3 结论与建议
本文设计了可使接头具有较大转动角度、保证其处于纯压弯受力状态的抗弯加载装置,并针对苏通GIL综合管廊工程盾构隧道管片接头(外径11.6 m,厚度550 mm)开展接头抗弯足尺试验,分别对轴力1 000~4 000 kN下接头抗弯力学参数进行量测和分析。基于试验结果得到以下结论:
1) 在纯压弯受力状态下,接头竖向位移、张开量、闭合量、弯矩-转角以及螺栓应力随着弯矩的变化曲线均相对较为平滑;不同弯矩作用方向下,接头张开高度随弯矩变化曲线可分不同变化阶段,其中正弯矩下可分为2个阶段而负弯矩下可分为3个阶段。
2) 采用文中接缝形式及螺栓连接方式时,轴力对于正弯矩下接头抗弯性能的影响大于其对负弯矩下接头抗弯性能的影响。
3) 采用文中接缝形式及螺栓连接方式时,正弯矩下接头抗弯性能与负弯矩下的有一定差异,且两者之间的差异随着轴力增大而减小。
在类似的接头试验中,建议将接头参数随弯矩变化规律与接头受力状态相结合,给出更适用于工程的定量指标。
