溢流式面板堆石坝坝身变形特性敏感性研究

耿 旭，李怀斌，刘 辛，党海霞，李 祥，渠继显，任国兵，吴 俊

(1.贵州新中水工程有限公司，贵阳 550000； 2.六枝特区水务局，贵州 六盘水 553400；3.贵州省建材产品质量监督检验院，贵阳 550000； 4.安顺市水利水电勘测设计院，贵州 安顺 561000)

1 概 述

克罗蒂面板堆石坝[1]是世界上首次在面板坝顶及下游坝面上布置开敞式溢洪道的工程。其加固措施为：在每一块叠瓦式底板的顶部布置水平阻滑板，同时还在底板和坝体之间布置水平锚筋[1-2]。根据克罗蒂坝的监测资料[1]，认为澳大利亚设计尚有富余；一些学者关于底板抗滑稳定的研究认为，基于静力分析理论，溢流面板堆石坝底板加固措施可作简化。据此，并结合已建工程的底板加固措施和施工的可行性，提出一种钢筋混凝土格栅式底板加固措施，即在每块泄槽底板顶端与坝体之间，布置水平外包混凝土的锚拉筋与埋在坝体内的预制混凝土横梁连接起来所形成的加固形式[2-6]。

文献[2-3]从探讨改变流速、加固措施长度和底板厚度等参数，分析稳定安全系数的变化规律；推导带水平加固措施的溢洪道底板静力抗滑稳定安全系数计算式，运用正交设计直观分析方法，对底板抗滑稳定敏感性进行研究，底板厚度和宽度对稳定性的影响较弱。溢流式面板坝坝体变形以及随之而来的裂缝导致渗漏和坝身稳定安全的问题，因此本文采取坝身变形特性来探讨加固措施中各因素之间的敏感性。文献[2]采用的流速为平均流速，而根据文献[7]和文献[8]溢流面上各断面的流速是变化的，为真实反映泄槽底板的水平拖拽力和脉动压力，本文采用分段求和法计算各断面的流速。

2 影响溢流面坝身变形特性敏感性分析

为探索锚固梁宽度、锚固梁高度、锚拉筋长度、锚固板长度、泄洪量以及堰顶插筋长度等因素对溢流面坝身变形的影响，采用正交设计方法，依托在建工程松树林水库，采用非线性弹性模型(邓肯E-B模型)进行分析。在建工程松树林水库溢流面典型剖面见图1，采用的邓肯E-B模型[11]参数见表1，各因素水平见表2，正交设计试验结果见表3。

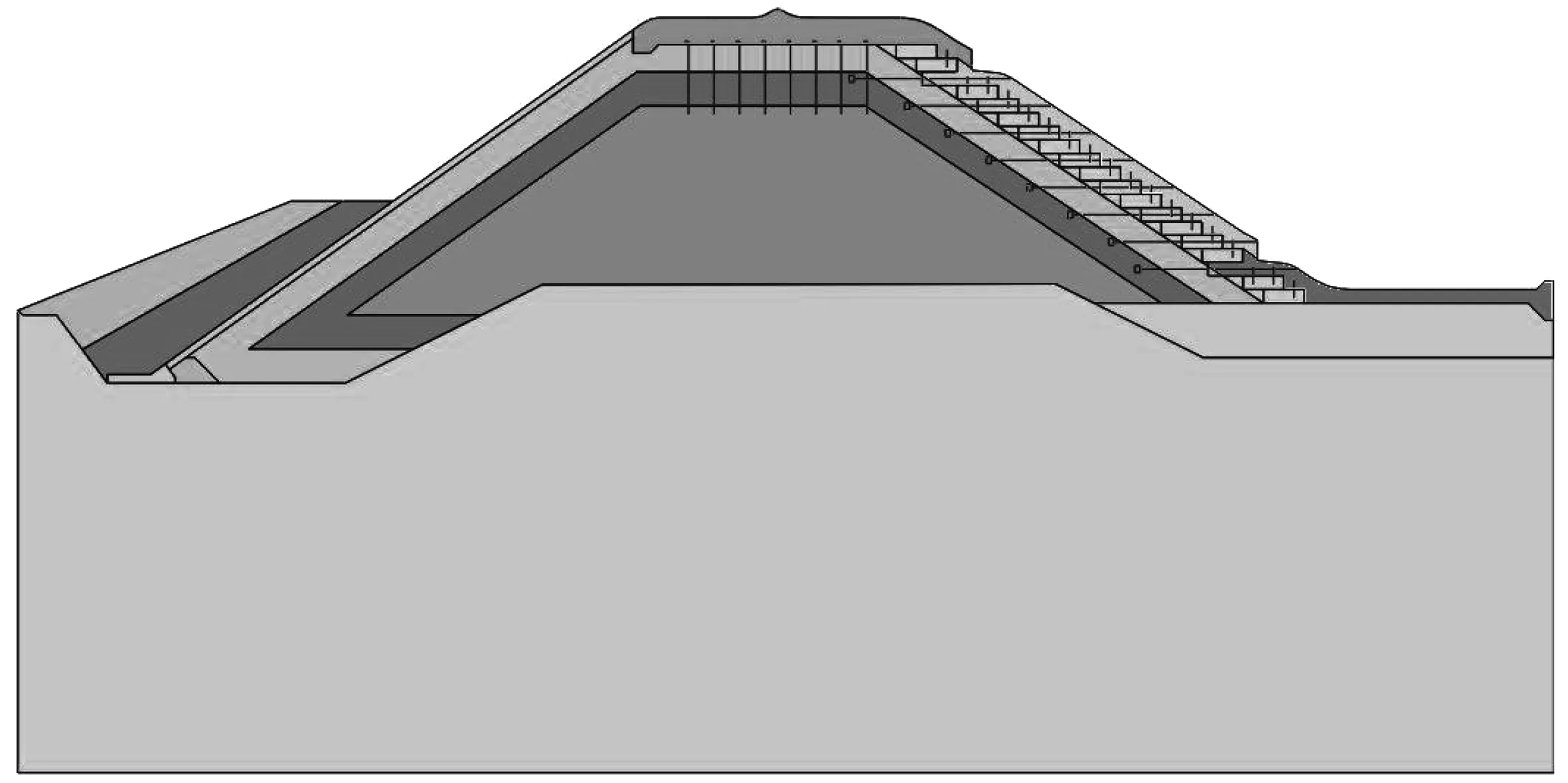
图1 松树林水库溢流面典型剖面

表1 松树林水库E-B模型参数

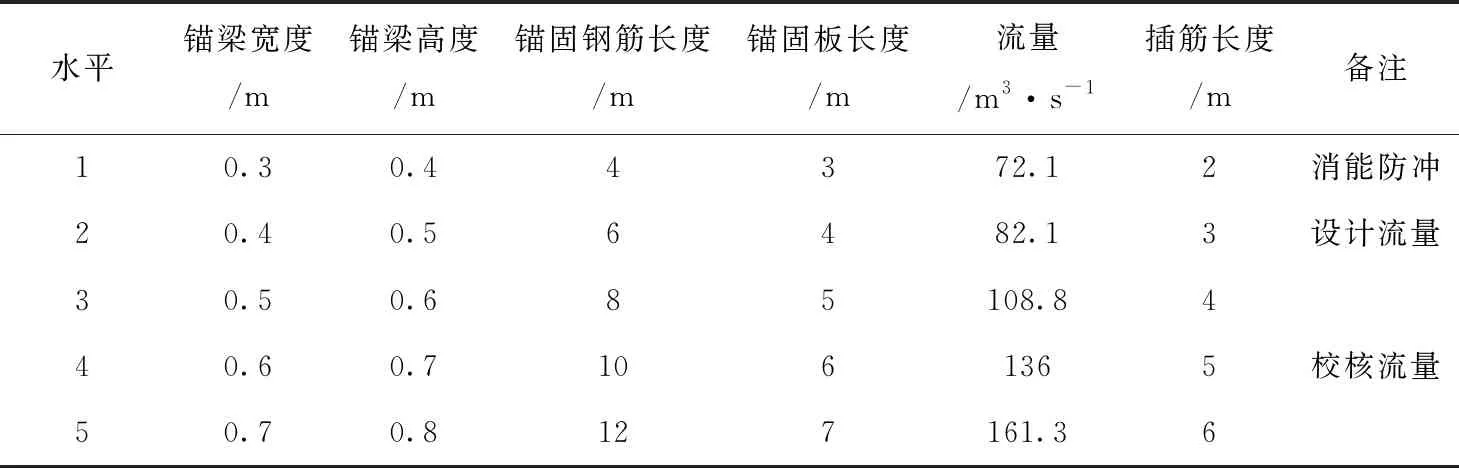
表2 各因素水平

表3 正交设计试验结果

续表3

各因素的水平改变对变形量的影响不同，极差越大的因素对变形量的影响越大[12]。表3中各因素对溢流面坝身变形的敏感性排序为：F(堰顶插筋长度)>C(锚固钢筋长度)>B(锚梁高度)>A(锚梁宽度)>E(流量)>D(锚固板长度)。

为便于探讨各指标随因素水平变化的情况，采用Oringin处理表3数据，见图2-图5。各点之间实际不是直线，但为便于分析，将各点用直线连接起来。为便于讨论各因素与变形量的关系，将C因素、D因素、F因素的数据均缩小10倍，E因素数据缩小100倍，以便放在同一图像中分析；图3中因素增量均为各水平减去第1水平。

图2 因素F与变形量变化规律

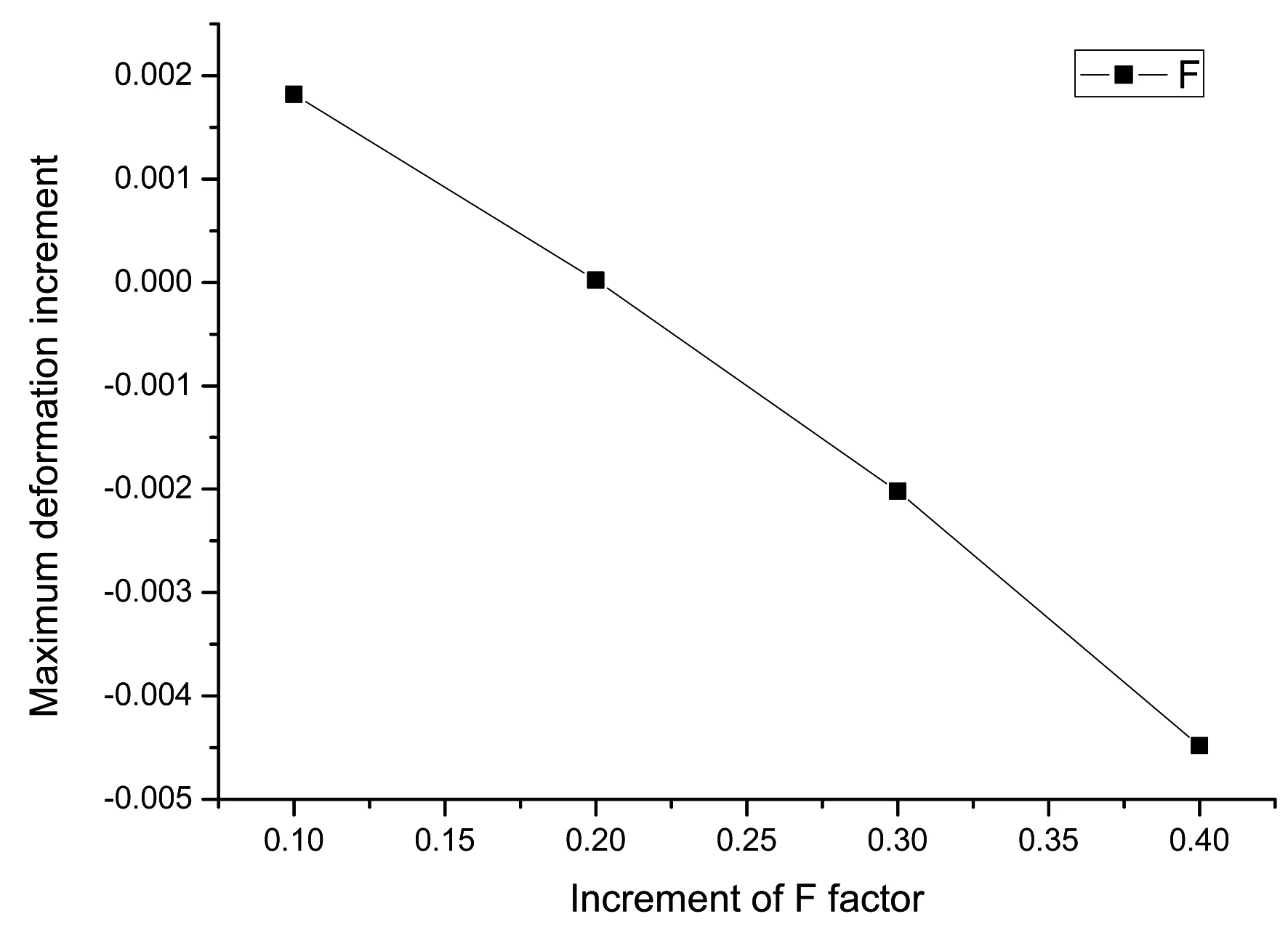
图3 因素F增量与变形量增量变化规律

图4 各因素与变形量变化规律

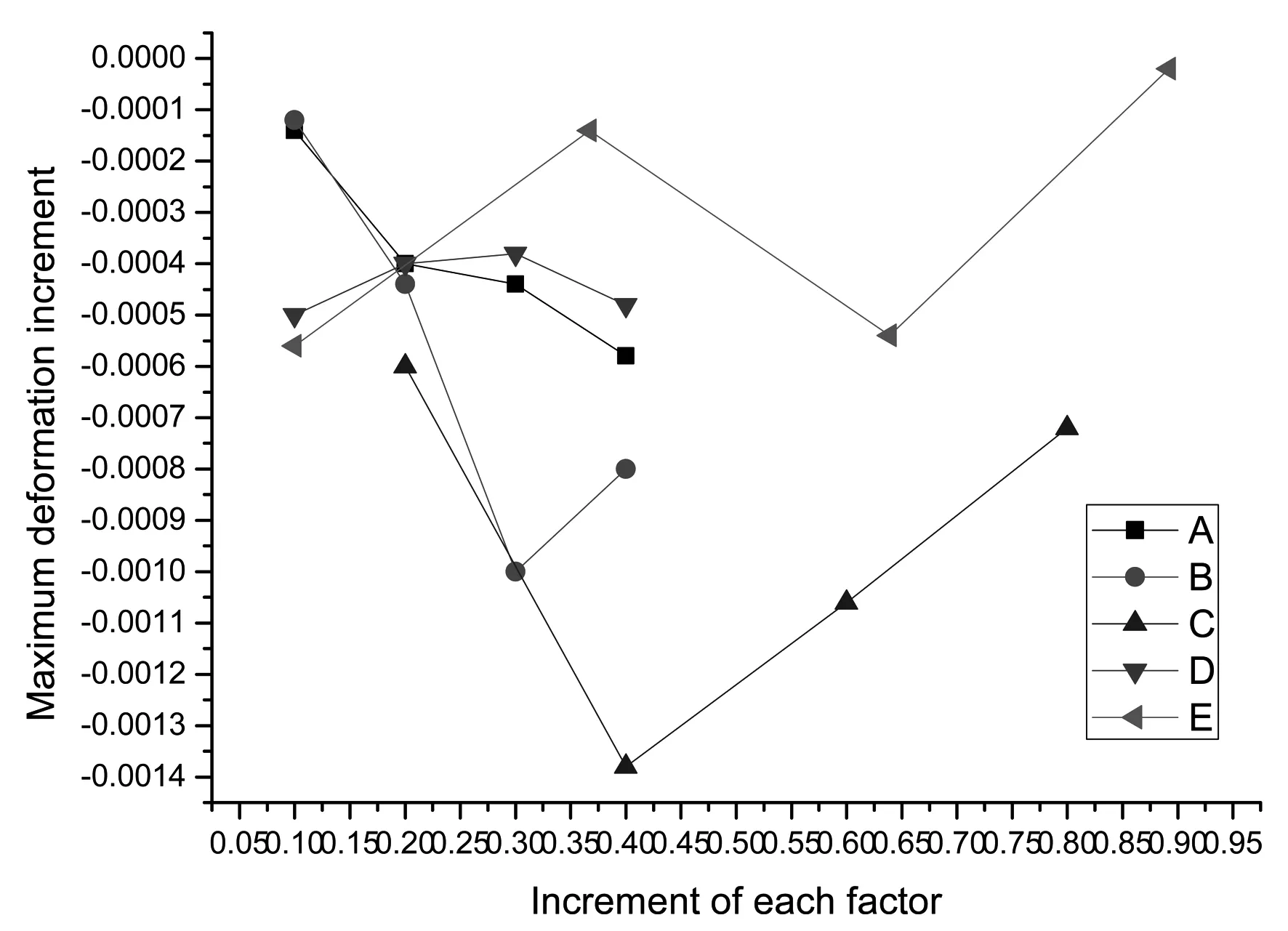
图5 各因素增量与变形量增量变化规律

结合表3及图2-图5分析各因素对变形量的影响：

1) 堰顶插筋长度F对变形量的影响。从表3得出，堰顶插筋长度的极差是最大的，堰顶插筋长度是影响变形量的最大因素。从图2中得出，堰顶插筋长度6 m时变形量最小0.084 98 m，2～3 m时变形量增加，3～6 m变形量减小，在3 m处出现极大值0.091 28 m。从图3中得出，堰顶插筋长度增量与变形量增量呈负增长趋势，拟合曲线方程为y=-0.002 09x+0.004 07，R2=0.994 98。根据试验结果，堰顶插筋长度较小时，不能有效减小变形，随着堰顶插筋长度增加，变形量降低；堰顶插筋长度增量与变形量增量呈负增长趋势。

2) 锚固钢筋长度C对变形量的影响。从表3得出，锚固钢筋长度的极差比堰顶插筋长度的极差小，排在第二，锚固钢筋长度是影响变形量的次要因素。从图4中得出，锚固钢筋长度4～8 m时，变形量随着锚固钢筋长度的增加而减小；锚固钢筋长度8～12 m时，变形量随着锚固钢筋长度的增加而增加；在锚固钢筋长度8 m处出现极小值0.087 9 m。从图5中得出，变形量增量在锚固钢筋长度8 m出现拐点，拐点之前的变形量增量随着锚固钢筋长度增量的增大而减小，拐点之后变形量增量随着锚固钢筋长度增量的增大而增大。根据试验结果，在一定范围内(小于锚固钢筋长度8 m)，增加锚固钢筋长度有利于减小变形量，锚固钢筋长度大于8 m，增加锚固钢筋长度反而增加变形量。

3) 锚梁高度B对变形量的影响。从表3得出，锚梁高度是影响变形量的第三因素。从图4中得出锚梁高度0.7 m时变形量最小，0.4～0.7 m变形量降低，而0.7～0.8 m时变形量增加，变形量最小值0.088 m。从图5中得出，锚梁高度增量在一定范围内随着增量的增大，变形量增量减小，突变点在0.6～0.8 m之间，随着锚固钢筋长度增量增加，变形量增量反而增加。根据试验结果，锚梁高度在一定范围内随着高度增加有利于减小变形量，但随着高度的继续增加，变形量反而增加。锚梁高度在0.7 m(含0.7 m)至0.8 m之间时，变形量最小。

4) 锚梁宽度A对变形量的影响。从表3得出，锚梁宽度的极差是0.000 58，锚梁宽度变化对变形量的影响比锚梁高度对变形量的影响小。从图4中得出，锚梁宽度与变形量呈负增长趋势，拟合曲线方程为：y=-0.002 09x+0.004 07，R2=0.994 98，增加锚梁宽度有利于降低变形量。从图5中得出，锚梁宽度增量与变形量增量呈负增长趋势，拟合曲线方程为：y=-0.001 36x-0.000 05，R2=0.913 83。根据试验结果，变形量随着锚梁宽度增大而减小，增加锚梁宽度有利于减小变形，且呈线性减小。

5) 流量E对变形量的影响。从表3得出，流量的极差0.000 56，流量变化对变形量的影响比锚固板长度对变形量的影响大。从图4中得出，在设计流量和校核流量时变形量均较小(0.088 22和0.088 24 m)；其他流量时的变形量均比设计流量和校核流量时的变形量大，呈W型。从图5中得出，流量增量与变形量增量呈W型。根据试验结果，流量与变形量呈W型，流量增量与变形量增量呈W型,下泄流量在设计流量和校核流量时变形量最小,其余流量下变形量均比设计流量下变形量大。

6) 锚固板长度D对变形量的影响。从表3得出，锚固板长度的极差最小，锚固板长度变化对变形量的影响最小。从图4中得出，随着锚固板长度的增加，变形量整体呈下降趋势，但在锚固板长度4 m处变形量出现极值0.088 38 m，锚固板长度大于4 m，变形量随着锚固板长度增加而增加。从图5中得出，变形量增量与锚固板长度增量呈抛物线型，拟合曲线为y=-0.000 05x2+0.000 26x-0.000 71，R2=0.992 31。根据试验结果，锚固板长度4 m时变形量最小，变形量增量与锚固板长度增量呈抛物线型。

3 结 语

基于正交设计试验，对影响溢流面坝身变形的锚固梁宽度、锚固梁高度、锚拉筋长度、锚固板长度、泄洪量以及堰顶插筋长度等因素进行极差分析，主要结论如下：

1) 各因素对溢流面坝身变形的敏感性排序为：F(堰顶插筋长度)>C(锚固钢筋长度)>B(锚梁高度)>A(锚梁宽度)>E(流量)>D(锚固板长度)。

2) 堰顶插筋长度较小时，不能有效减小变形，随着堰顶插筋长度增加，变形量降低；堰顶插筋长度增量与变形量增量呈负增长趋势。在一定范围内(小于锚固钢筋长度8 m)，增加锚固钢筋长度有利于减小变形量，锚固钢筋长度大于8 m，增加锚固钢筋长度反而增加变形量。锚梁高度在一定范围内随着高度增加有利于减小变形量，但随着高度的继续增加，变形量反而增加。锚梁高度在0.7 m(含0.7 m)至0.8 m之间时，变形量最小。变形量随着锚梁宽度增大而减小，增加锚梁宽度有利于减小变形，且呈线性减小，拟合曲线方程为y=-0.002 09x+0.004 07，R2=0.994 98。流量与变形量呈W型，流量增量与变形量增量呈W型,下泄流量在设计流量和校核流量时变形量最小,其余流量下变形量均比设计流量下变形量大。锚固板长度4 m时变形量最小，变形量增量与锚固板长度增量呈抛物线型。

3) 本文讨论的变形是坝体总变形的最大值，试验中考虑不同土体之间的接触以及加固措施中各因素之间的接触，试验结果可能与不考虑接触的试验结果有差别。本文讨论采用的邓肯E-B模型，试验结果可能与双屈服面弹塑性模型的试验结果有差别。