考虑多约束的多区域动态经济调度
2020-07-31李锦焙
李锦焙
(广东电网有限责任公司佛山南海供电局,广东 佛山 528000)
0 引 言
电力系统优化调度[1-4]问题是通过合理分配各个发电机组的出力实现最优组合来实现运行成本的经济性。电力系统动态优化调度通过缩短调度时间跨度实现了优化的实时性,使优化结果更加贴近实际电网的运行。随着电力系统规模的扩大以及用电负荷中心的分散,为了确保供电网络的可靠性,多个负荷中心互联的多区域电力系统对电力系统安全稳定运行至关重要。多区域电力系统互联有利于提升系统的稳定性和可靠性,降低电网运行成本,同时使得电网的调度更加灵活。相对于静态优化调度,电力系统多区域动态优化调度(Multi-area Dynamic Economic Dispatch,MADED)的研究难点在于发电机组的机械特性使得其无法在瞬间调整出力以满足负荷的要求,为此需要在运行过程中考虑发电机组的爬坡率约束。
电力系统多区域静态优化问题[5]已经得到较为深入的研究。早期,数学方法是研究该课题的主要方法,例如:分解法[6]、直接搜索方法[7]。电力系统动态优化问题是一个高纬度、多维度、非凸以及多约束的优化问题,显然,传统的数学优化方法无法高效地解决该类问题。随着计算机科学以及人工智能算法的发展,各类型人工智能算法被用于求解电力系统优化问题,例如:人工蜂群优化法[8]、TLBO算法[9]、GBABC算法[10]。对于静态和单一区域的优化调度,专家学者的研究已经较为深入且充分,但对于MADED问题的研究则相对较少,目前仅有以下两种方法进行了初步的尝试:QOGSO算法[11]、Decentralized Optimization算法[12]。人工智能算法求解优化问题的原理,使得其在解决复杂的优化问题时,比传统数学方法更容易获得更优结果。但是,大多数优化算法无法彻底解决在优化过程中出现的局部最优、种群缺乏多样性等问题。为此,需要采取手段对现有算法进行改进,以便获得更加优质的优化结果。
基于NW模型的邻域特性,文章提出采用NW小世界模型[13]对差分量子粒子群(Differential Evolution Particle Swarm Optimization,DEPSO)算法进行改进,得到一种NW小世界差分粒子群(NW Small-world Differential Evolution Particle Swarm Optimization,NWDEPSO)算法。DEPSO算法是将差分进化(Differential Evolution,DE)算法[14]和量子粒子群(Particle Swarm Optimization,PSO)算法[15]进行混合,但由于DEPSO算法在在优化过程中不可避免地会出现种群多样性不足、局部最优等缺陷,因此,引入 NW小世界邻域模型对该混合算法进行改进。
1 数学模型
对MADED问题进行研究的目的是在满足各类型约束的前提下实现优化结果的经济性,该问题的数学模型如下。
1.1 费用函数
费用函数如式(1)所示。
(1)
式中:F(Pij,t)是单个发电机组的费用函数;T为调度周期;N为区域数量;Mi为区域i的机组数;Pij,t为第t个时段区域i中第j台机组的实际输出功率。
1.1.1 考虑阀点效应的费用函数
汽轮机的机械特性决定了其费用曲线不能是一条光滑的二次函数曲线,为了使优化结果更加精确,需要将发电机组的阀点效应体现于费用曲线中,具体如图1和式(2)所示。
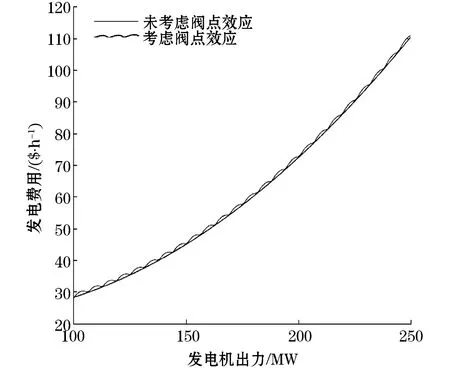
图1 考虑阀点效应的发电成本曲线
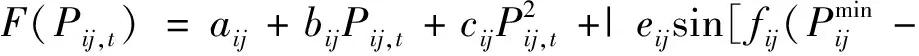
Pij,t)]|
(2)
1.1.2 机组考虑多燃料和阀点效应的成本函数
发电组的多燃料特性指的是根据不同出力情况选择不同类型的燃料。同时考虑多燃料特性和阀点效应的发电成本曲线如图2所示,发电成本函数如式(3)所示。
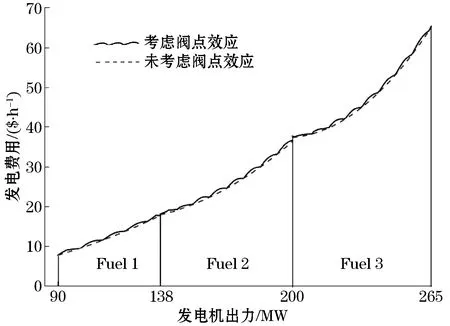
图2 考虑多燃料和阀点效应的发电成本曲线
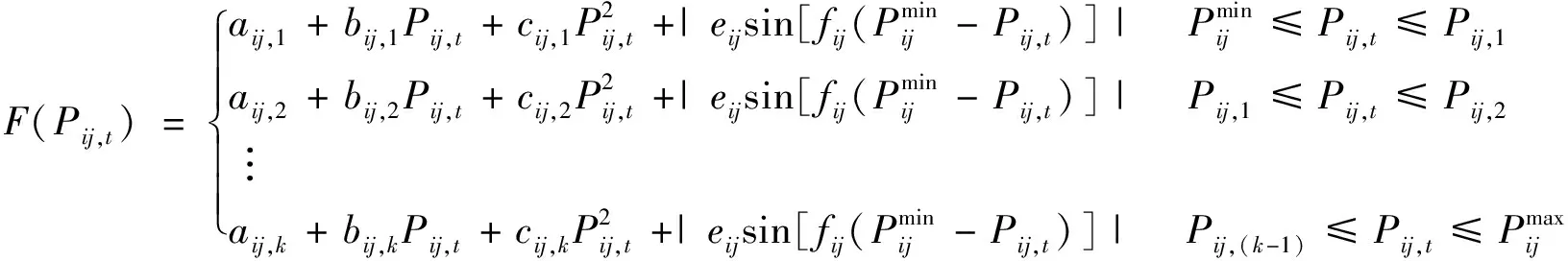
(3)
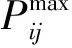
1.2 优化问题约束条件
1)发电机组运行在允许运行区间是确保系统稳定运行的前提,其中,第t时段区域i中第j台机组的功率限制为
2)爬坡率约束为
式中:URij和DRij分别为区域i中第j台发电机允许出力瞬间变化的幅度。
3)功率平衡为
式中:PLi,t为该区域在该时段的网损;PDi,t为负荷需求;Tir,t为区域i和区域r之间联络线的传输功率。
4)各区域在各时段的网损为
(4)
为简化求解过程,采用式(4)求解各区域的网损,具体网损系数见文献[11]。
5)传输线容量限制为
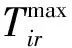
2 NW小世界差分粒子群算法
2.1 NW小世界网络
目前,主流的小世界模型有NW小世界模型和WS小世界模型[13],其中,NW模型是在WS模型基础上进行改进得到的,它避免了WS模型在构造网络过程中产生孤立节点的缺陷,提高了网络的连通性。
2.2 DE算法
DE算法的种群进化是通过扰动、交叉变异和优胜劣汰实现的。
2.3 PSO算法
PSO算法是目前主流的群优算法,被用于求解各类型优化问题。其基本的算法步骤如下:
步骤1:初始化种群。
步骤2:根据适应度函数求出初始种群中每个个体的适应度并形成初始种群全局最优解。
步骤3:更新每个粒子的位置和速度。
步骤4:判断是否达到迭代上限,达到则结束算法,否则转到步骤2继续执行。
3 NWDEPSO算法的原理
NWDEPSO算法通过NW小世界模型进行邻域划分,利用DEPSO算法对各个邻域内的粒子进行优化,优化结果较原始的DE算法和PSO算法更具优势,其优化步骤主要如下:
步骤1:通过随机方式形成初始矩阵,得到初始种群。
步骤2:构造NW小世界网络。
①无差异地对初始种群的各个粒子进行编号;
②进行第1次迭代时,节点的度为初始值,如果迭代次数大于1,则根据随机加边规则确定新的度构造邻接矩阵。
步骤3:采用适应度计算式(5)计算邻接矩阵中每个粒子的适应度。
(5)
式中:penish为惩罚系数。惩罚系数可以确保满足负荷平衡的粒子对应的适应度总是比不满足的负荷平衡的粒子对应的适应度好,从而为种群的进化提供方向。
步骤4:进行粒子位置和速度更新。
步骤5:进行突变操作。
步骤6:交叉操作。
步骤7:选择操作。
在更新过程中,产生的粒子有可能出现越限的情况,需要采取相应措施对其进行修正,具体方法如下。
①约束处理
根据考虑的约束条件对粒子进行修正。采用式(6)和式(7)对发电机组出力和区域之间联络线传输功率进行校正。爬坡率约束与优化的时段相关联,当调度时段不大于1时,不需要进行修正,当调度时段大于1时,采用式(8)对其进行修正。
(6)
(7)
Xi,t=
(8)
②采用式(5)重新计算经校正后粒子的适应度,并采用贪婪策略更新种群。
步骤8:确定是否完成对所有邻接矩阵的遍历,是则进入步骤9,否则回到步骤3。
步骤9:判断是否已完成规定的迭代次数,是则停止算法运算并输出最优解,否则用式(9)计算随机加边概率并执行随机加边操作,回到步骤2继续进行迭代运算。
(9)
其中:Gen和maxgen分别是当前迭代次数和最大迭代次数。
文章采用NWDEPSO算法求解MADED问题,算法实现的流程图如图3所示。
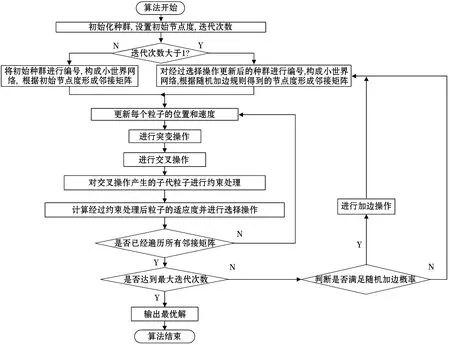
图3 NWDEPSO算法流程图
4 算例分析
使用Matlab 2010a进行仿真,参数设置为:种群大小popsize=20,最大迭代次数maxgen=1 500。
为了验证NWDEPSO算法解决MADED问题的有效性,文章采用NWDEPSO算法对10机组3区域系统进行仿真,该算例的机组数据、24个时段的负荷需求、各个区域的网损系数、考虑因素和区域划分来自文献[11]。NWDEPSO算法求解该算例的优化结果如表1所示,NWDEPSO算法求解该算例在24时段的最优调度方案如表2~4所示,图4为10机组3区域系统区域分布图,算法优化过程的收敛曲线如图5所示,图6为NWDEPSO算法单独对算例进行50次仿真试验得到的优化结果。
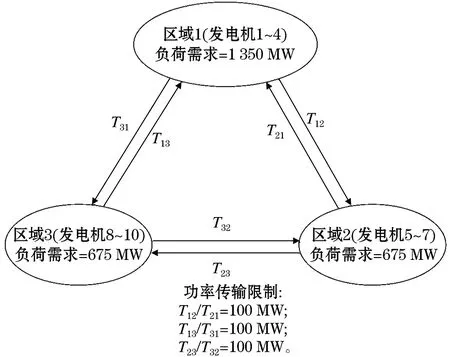
图4 10机组3区域系统区域分布图
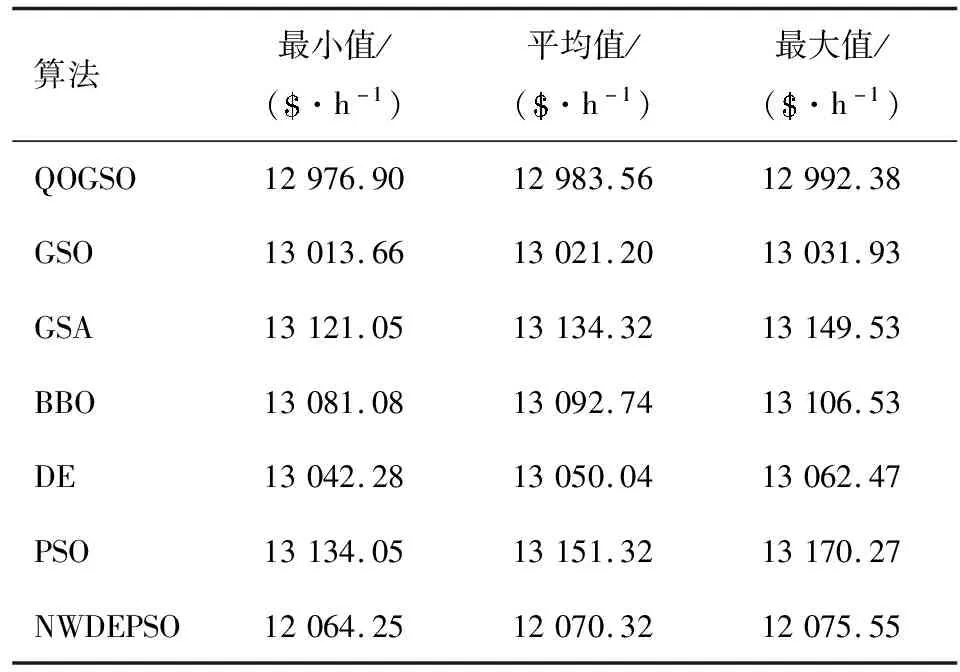
表1 NWDEPSO算法与其它算法对比
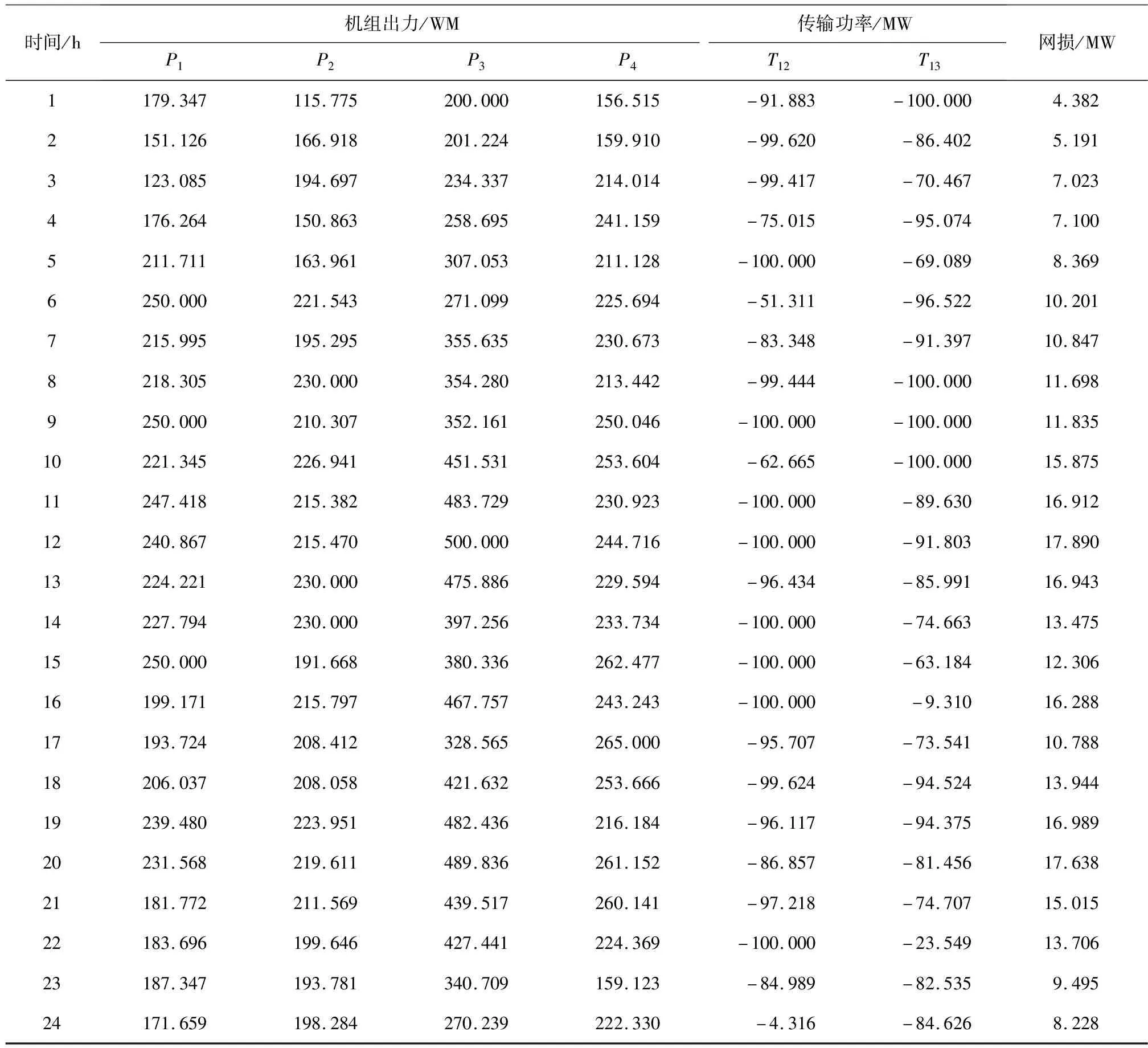
表2 区域1各时段的优化结果
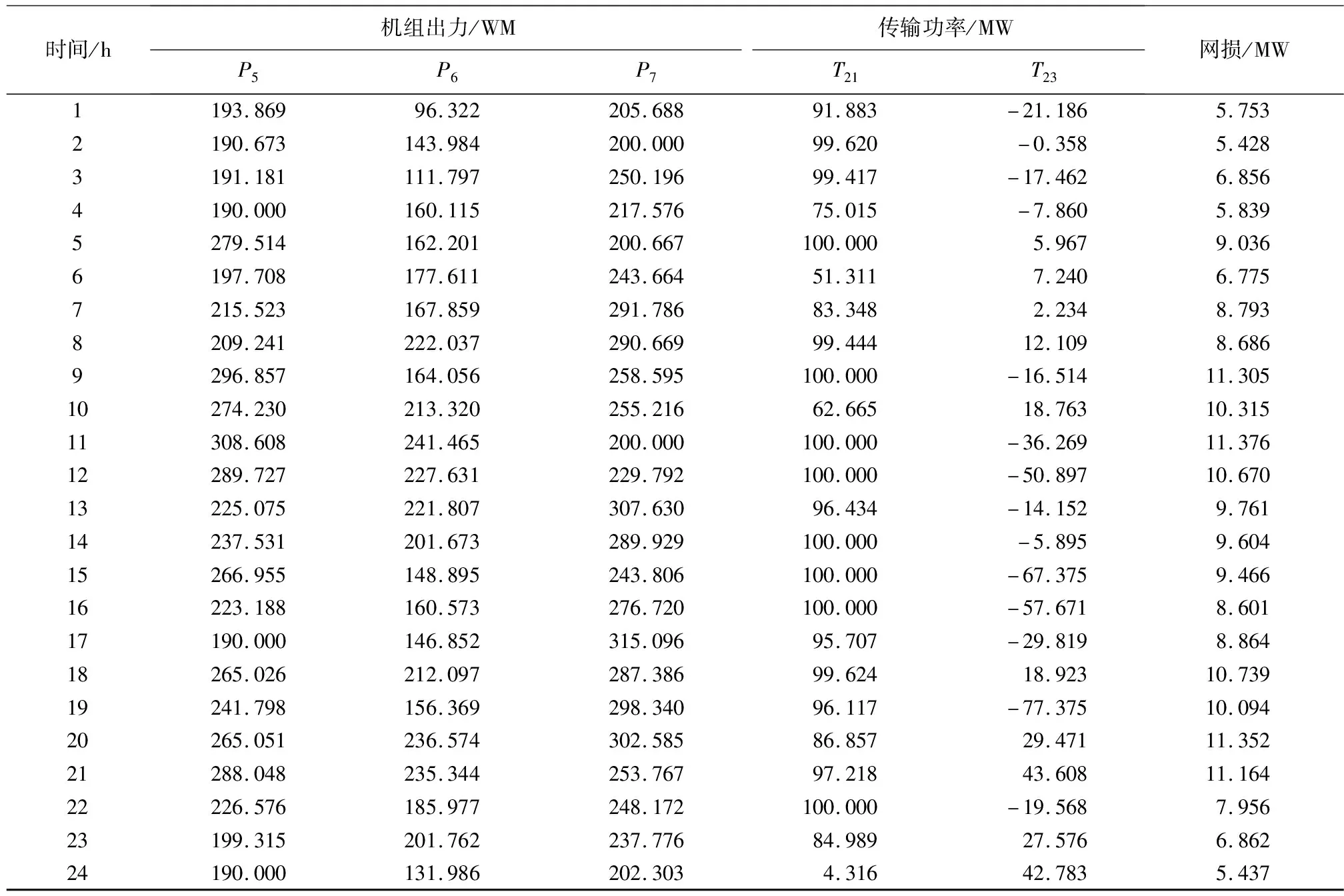
表3 区域2各时段的优化结果
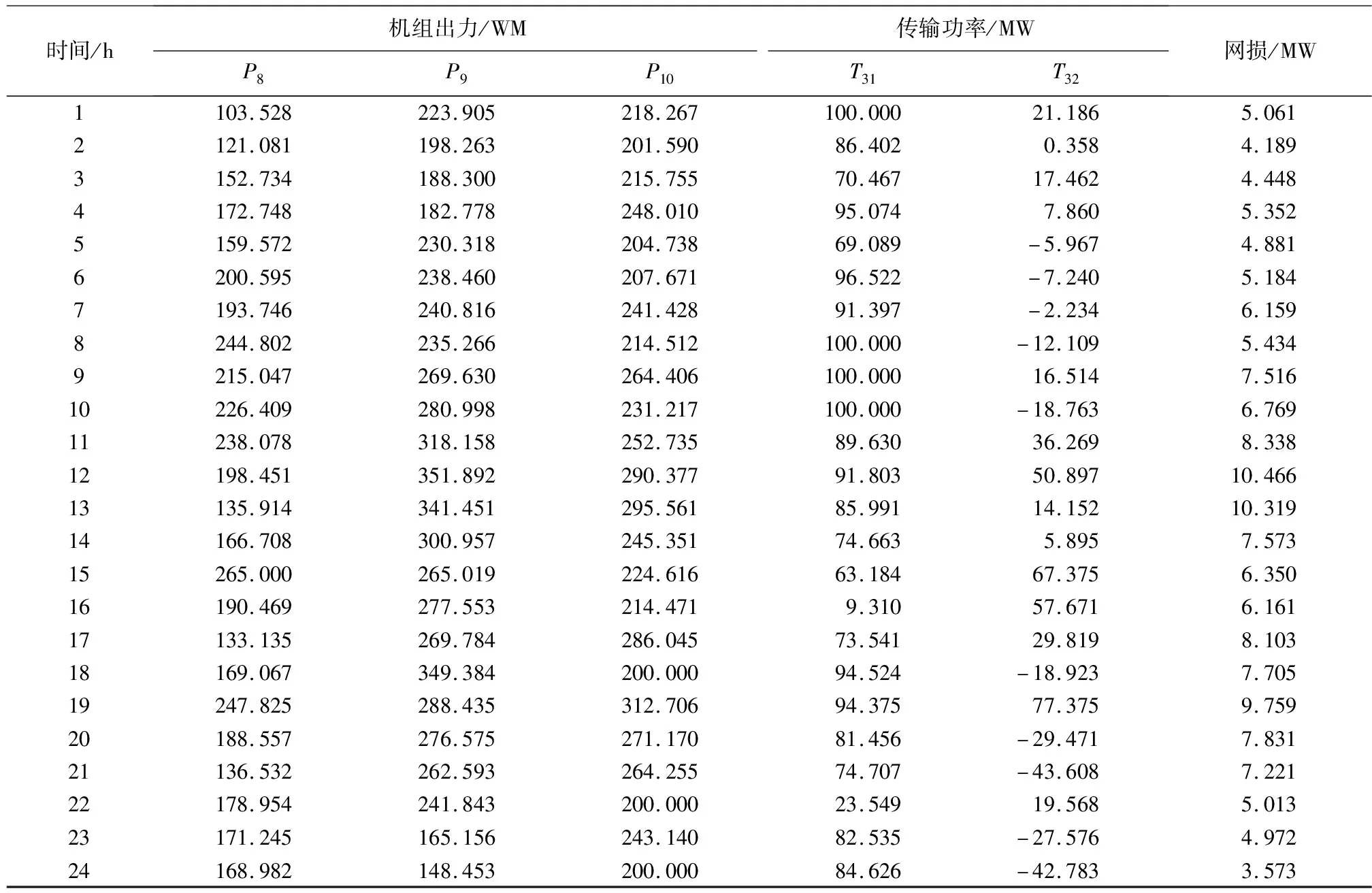
表4 区域3各时段的优化结果
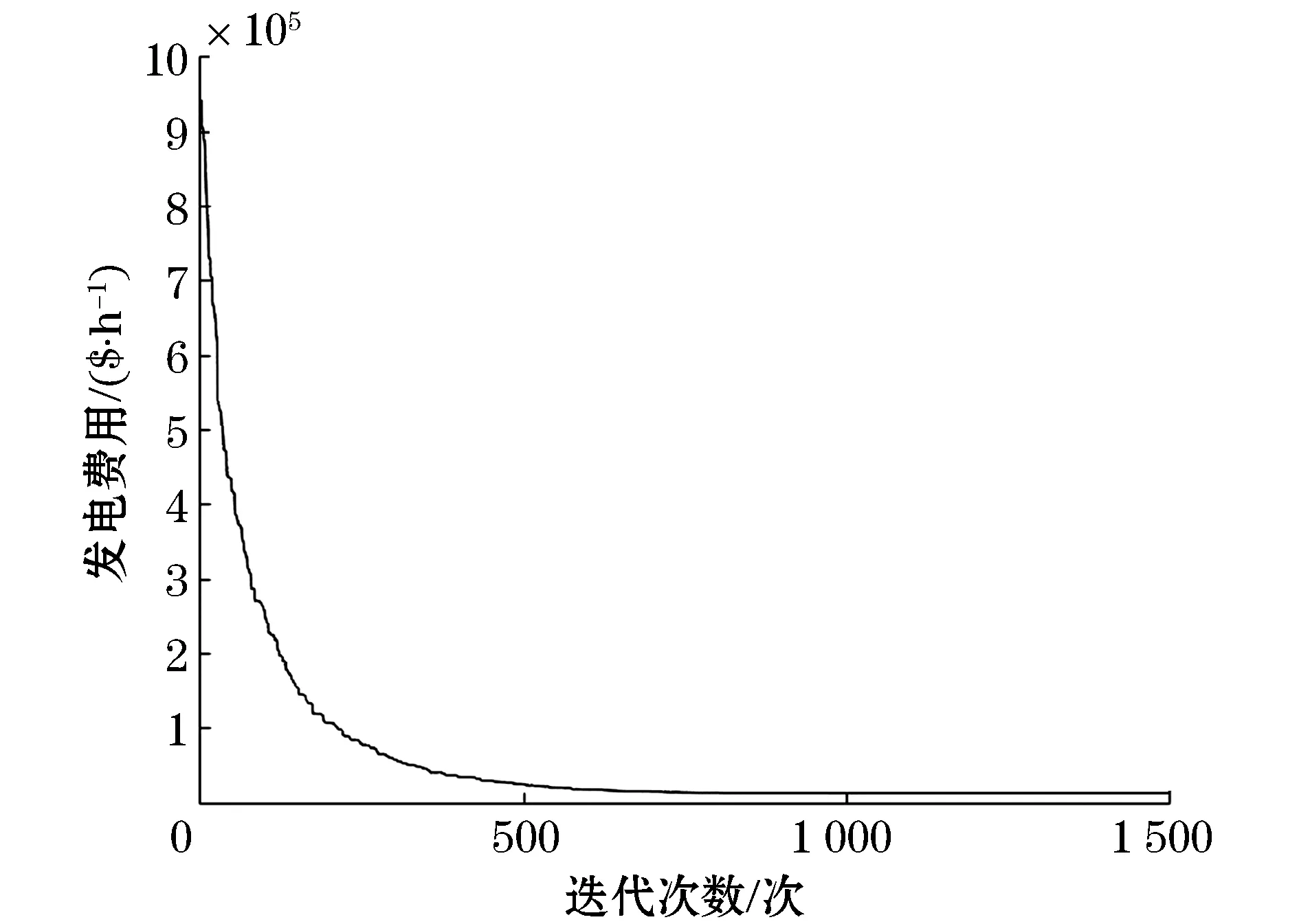
图5 NWDEPSO算法的收敛曲线
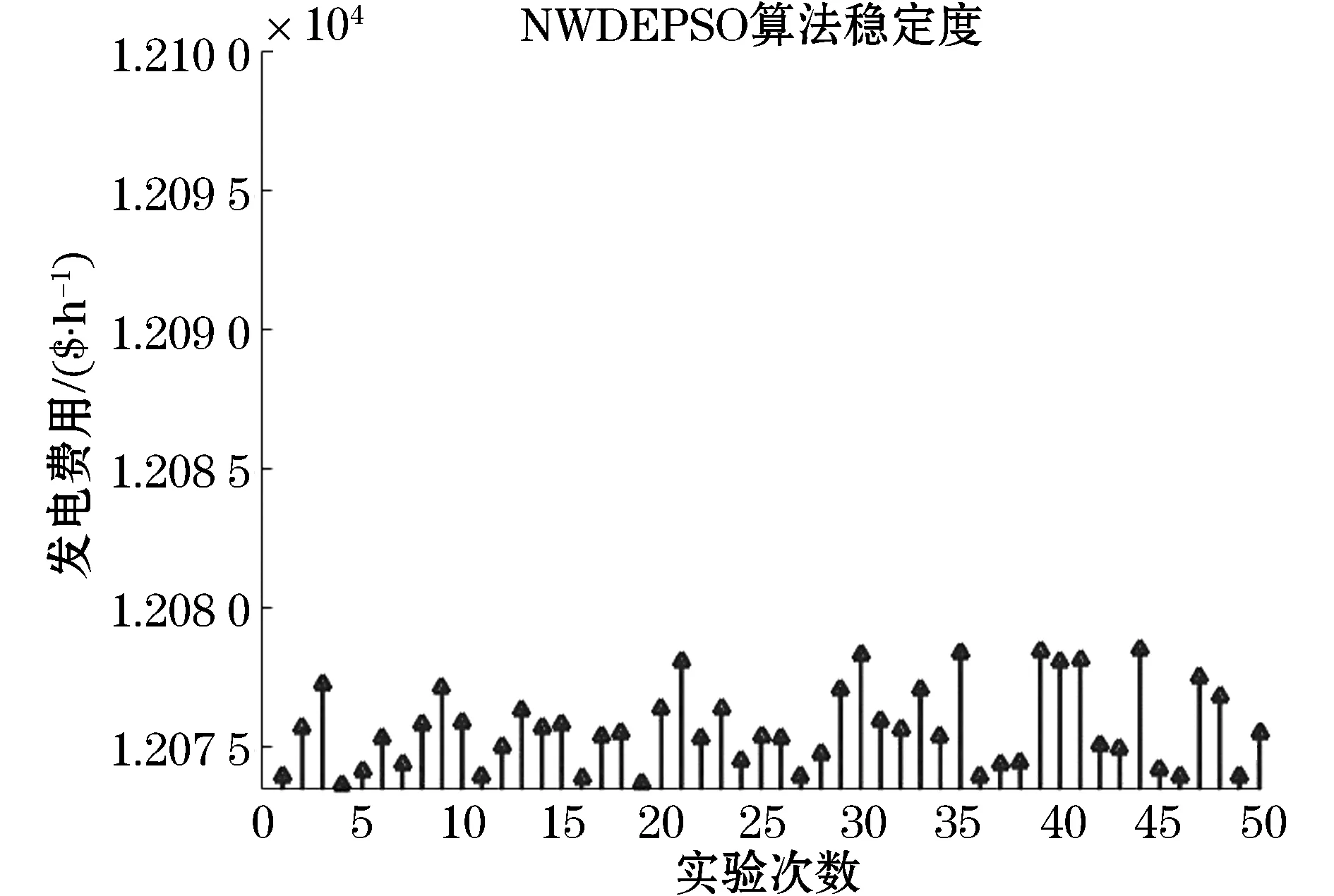
图6 NWDEPSO算法重复运行50次结果分布图
5 结 语
在小世界模型、差分算法、粒子群算法的基础上,提出了小世界差分粒子群算法,并将其应用于多约束多区域动态经济调度中,得出了如下结论:
1)改进后的NWDEPSO算法适用于求解高维、非凸、多约束的优化问题。
2)引入NW小世界网络对DEPSO算法进行改进,实现了邻域之间粒子信息的交流和共享,提高了DEPSO算法的求解复杂的优化问题的能力。
3)算例表明,用所提算法研究多区域动态经济调度问题,不仅操作简单,而且得到的优化方案更加具有优势。因此,所提方法所得到的解是经济可行的。
