基于Krigingiging法的淮北平原浅层地下水监测网优化分析
2020-07-31洪叶青
洪叶青
(安徽省地质环境监测总站, 安徽合肥 230001)
0 引言
淮北平原地处安徽省北部,为黄淮海平原南侧,总面积约42400km2。由于地表水资源匮乏,该区主要以开采地下水资源供水。长期持续的地下水资源开采,导致该区地下水位下降。该区于20世纪80年代初开始开展地下水监测工作,目前已建成的地下水监测网络共计有9条北东—南西、13条北西—南东的骨干监测剖面,监测密度约200km2/点。随着该区经济社会的发展,地下水监测工作程度的要求愈加提高,地下水监测网络的进一步优化布置就显得尤为重要。Kriging法是一种对时空分布变量求最优、线性、无偏内插估计量的方法。采用Kriging法对淮北平原水文地质单元的地下水现状监测网进行合理布置与优化,可有效避免人为因素而造成的随意性,得到较为准确合理的优化结果。
1 Kriging法原理简介
Kriging法是依据协方差函数对随机过程/随机场进行空间建模和预测(插值)的回归算法[1]。在特定的随机过程中,Kriging法能够给出最优线性无偏估计,因此在地统计学中也被称为空间最优无偏估计器[1]。由于两个监测点相距较近的监测数据比相距较远的监测数据更接近,所以距离越小,两点间数值差异就越小。两点间距离的大小决定了两点间数值差异的大小,进而说明了空间相关性的存在。岩层和地下水流动的空间连续性,使得地下水在空间上并非彼此独立且均匀,而是在某一特定区域内彼此相关。
利用Kriging法可以对现有监测孔点之间的地下水水位用空间插值法进行计算,插值的精度取决于监测井的个数与位置。插值法不仅能给出插值,还能提供插值的误差值,再根据误差标准差的大小,可以有效确定误差标准差较大的区域,进而对现有监测网进行优化布置。其原理如下:
Kriging法插值Z*0定义为观测值的加权平均值,即:

插值的精度定义为插值的误差的方差,即:

Zi—为在位置 xi(i=1,2,…,n)的观测值;
γ(xi-x0)—为方差函数(Variogram)值;
μ—为拉格朗日乘子。
利用Kriging法对现有监测网进行优化设计的方法是:通过事先给定的插值误差均方差临界值,在计算插值误差标准差高于临界值的区域内,增加新的监测点,直至全区计算的插值误差标准差逼近临界值,从而设计最优监测网[2]。具体流程见图1。
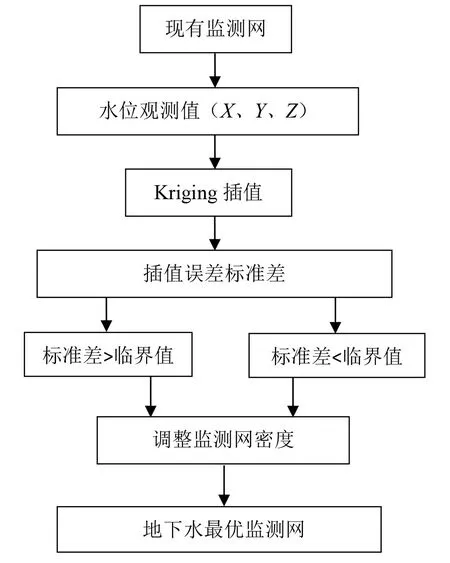
图1 克里金模拟方法优化监测网流程Figure 1.Kriging simulation method to optimize the flow of monitoring network
2 淮北平原现有监测网介绍
安徽省淮北平原现有浅层松散岩类孔隙水监测点共计163个,总监测控制面积达42400km2,分布于淮北平原6个地市,具体分布情况见表1、图2。

表1 淮北平原浅层地下水监测点分布统计Table 1.Distribution of shallow groundwater monitoring stations in the Huaibei Plain

图2 淮北平原浅层地下水监测点分布图Figure 2.Distribution map of shallow groundwater monitoring stations in the Huaibei Plain
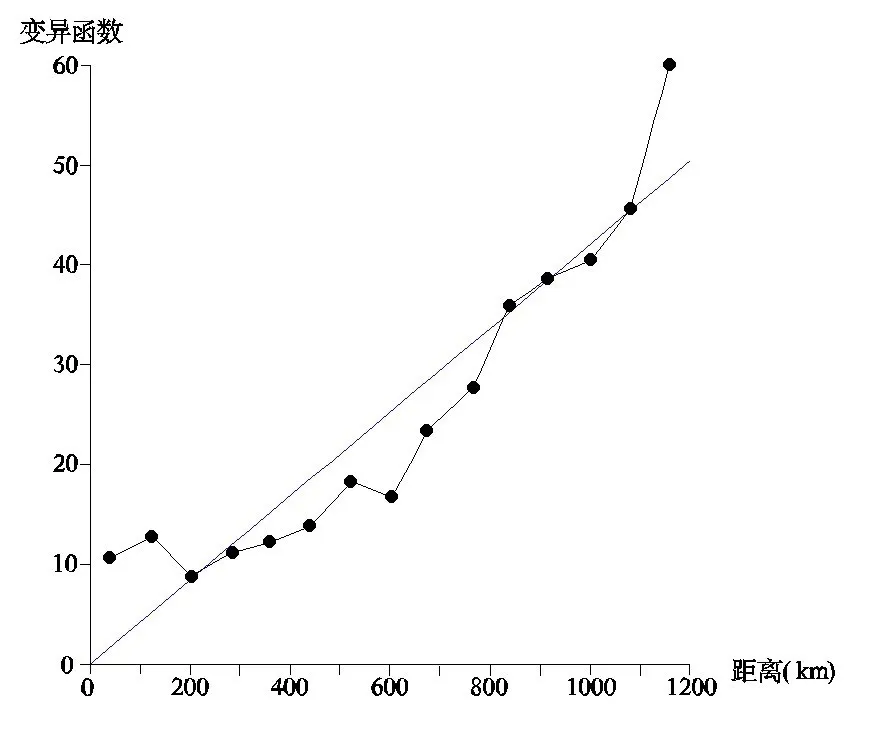
图3 模拟的最优线性变异函数图Figure 3.Simulated optimal linear variogram

图4 淮北平原现状监测站点Kriging标准差差值等值线图(单位:m)Figure 4.Contour map of Kriging standard deviations of current monitoring stations in the Huaibei Plain(unit:m)
3 利用Kriging法对现有监测网进行优化设计
根据2018年淮北平原浅层监测点水位动态监测资料,利用Surfer软件选择线性变异函数进行Kriging插值模拟。通过反复模拟确定线性变异函数最优坡度/斜率值为0.0419,各向异性比率1.0,见图3。
利用Kriging插值模拟计算的标准差差值,确定需增加布置的监测点位置(见图4)。由图可见,监测点分布越少的区域标准差差值越大。因此,对监测网密度的优化思路即在标准差差值大的区域布置新的监测点。
根据模拟结果,在Kriging标准差差值较大的区域共计增加20处监测站点(图5中三角形符号),监测站点总数增至183个,见图5。
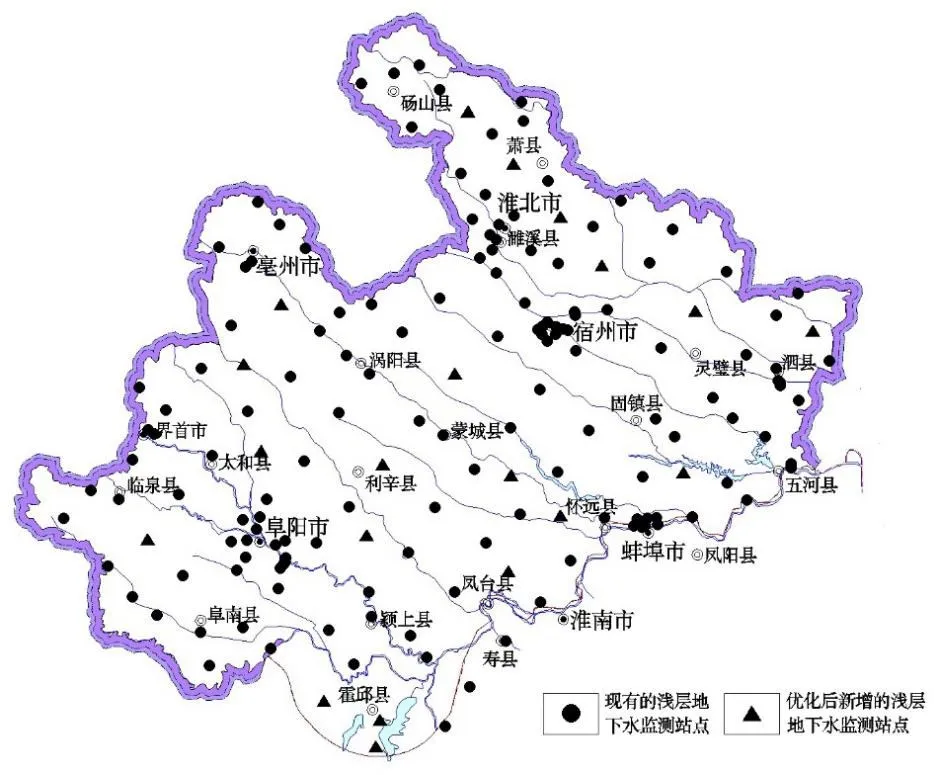
图5 优化设计后地下水监测点分布图Figure 5.Distribution map of groundwater monitoring stations after optimized design
利用Kriging插值法对优化后的监测网进行分析评价,对比优化前后插值的残值误差大小,评价优化结果。由图6优化后监测站点Kriging标准差差值等值线图可见,新增加的监测井明显降低了水位插值的误差,优化设计较为合理。
4 结语
利用Kriging插值法可以对现有监测网的精度进行计算,准确确定监测网精度较低的区域,从而对现有监测网进行优化,获得精度较高的地下水动态监测数据,以达到监测区域地下水变化趋势的目的。
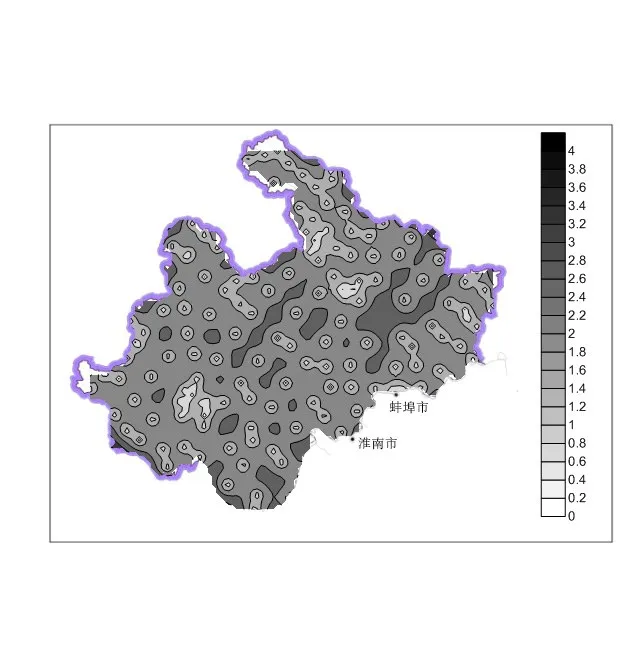
图6 优化后监测站点Kriging标准差差值等值线图Figure 6.Kriging standard deviation contour map of optimized monitoring stations
