典型多目标优化算法在控制优化中的适用性研究
2020-07-30李羿良张英陈冠宇赵梦薇林超
李羿良 张英 陈冠宇 赵梦薇 林超


摘 要
多目标优化算法可以对控制系统的多个控制目标进行控制优化,具有普适性强、灵活性高和优化结果全面的优点。多目标优化算法种类较多,不同种类的算法针对具体问题求解的适用性存在差异[1]。针对控制优化问题的求解,对三种典型多目标优化算法的适用性进行研究。选择三项不同类型的应用案例,分别对三种典型多目标优化算法的求解性能进行试验与分析,在此基础上确定出一种最适用于控制优化的多目标优化算法,可对多目标控制优化问题中算法的选择提供指导和参考。
关键词
多目标优化算法,控制优化,适用性研究
中图分类号: U463.33 文献标识码: A
DOI:10.19694/j.cnki.issn2095-2457.2020.19.078
0 引言
控制优化问题的优化目标往往不止一个,当多个优化目标之间存在冲突时,该控制优化问题就成为多目标优化问题。通常多个优化目标难以同时达到绝对的最优,但可以达到相互制约条件下的相对最优,即Pareto最优。所有Pareto最优解的集合形成了多目标优化问题的最优边界,因此求解多目标优化问题的本质是找到该问题的最优边界。理论上,采用多目标优化算法对多目标优化问题进行求解,可以无限逼近最优边界从而得到理论最优解集。但由于多目标优化算法种类较多,在解决不同的优化问题时,不同的算法之间存在较大的性能差异。适用性更好的算法可以在得到更好结果的同时节省计算时间和计算力。因此需要对不同多目标优化算法在控制优化中的适用性进行研究。根据所采用智能优化算法的不同,可以对多目标优化算法进行分类。目前常用的多目标优化算法包括多目标进化算法、多目标蚁群算法和多目标粒子群算法[2]。为了避免算法自身缺陷对控制参数优化带来的不利因素,确保优化效果,本文利用标准测试函数和两个典型控制优化模型对这三种典型多目标优化算法分别进行性能试验和结果分析,在此基础上确定出一种最适用于控制优化的多目标优化算法。
1 三种典型多目标优化算法的描述[3]
1.1 多目标优化问题与多目标优化算法的一般化描述
多目标优化算法是一种以Pareto支配关系为基础对多目标优化问题进行求解的算法。多目标优化算法的核心步骤是针对每一次迭代后的种群,依据Pareto支配关系寻找当前Pareto最优解集,然后通过智能优化算法的更新法则对该解集进行迭代更新,迭代完成后最新的Pareto最优解集就是优化问题的解。
1.2 多目标进化算法
多目标进化算法种类繁多,虽然每个种类的具体算法各不相同,但它们的基本思路是一致的:通过对种群B(t)执行评价、选择和变异等操作产生下一代种群B(t+1);在每一代进化过程中,首先将种群B(t)中所有的非劣解个体都复制到外部集A(t)中,然后运用截断算子剔除A(t)中的受支配解和一些距离较近的非劣解,以尽快得到分布均匀的下一代外部集A(t+1);并且按照精英集中度Pe(t)從A(t+1)中选择一定数量的优秀个体与A(t)种群交配;在进化结束时,将外部集中的非劣解个体作为最优解输出。多目标进化算法的一般框架如图1所示。
本文测试的典型多目标进化算法采用Matlab2010b中自带的NSGA2函数,即改进型非劣排序遗传算法,于2002年提出。该算法作为一种典型多目标进化算法,常被作为其他多目标优化算法的比较对象[4]。
1.3 多目标蚁群算法
蚁群算法通过模拟蚁群通过信息素寻找目标的方式进行寻优。当一只蚂蚁移动到一个新的点时,会根据此点对应的目标函数值释放信息素,同时信息素会随着迭代步数的增长慢慢消散。蚁群的移动以搜索范围内各点积聚的信息素作为参考因素,趋向于信息素积聚较多的点移动。由此形成一种正反馈机制,即最优路径上的信息素数量越来越大,而其他路径上的信息素数量却会随着迭代步数增长而消减,最终整个蚁群会找出最优路径,实现优化问题的求解[5]。
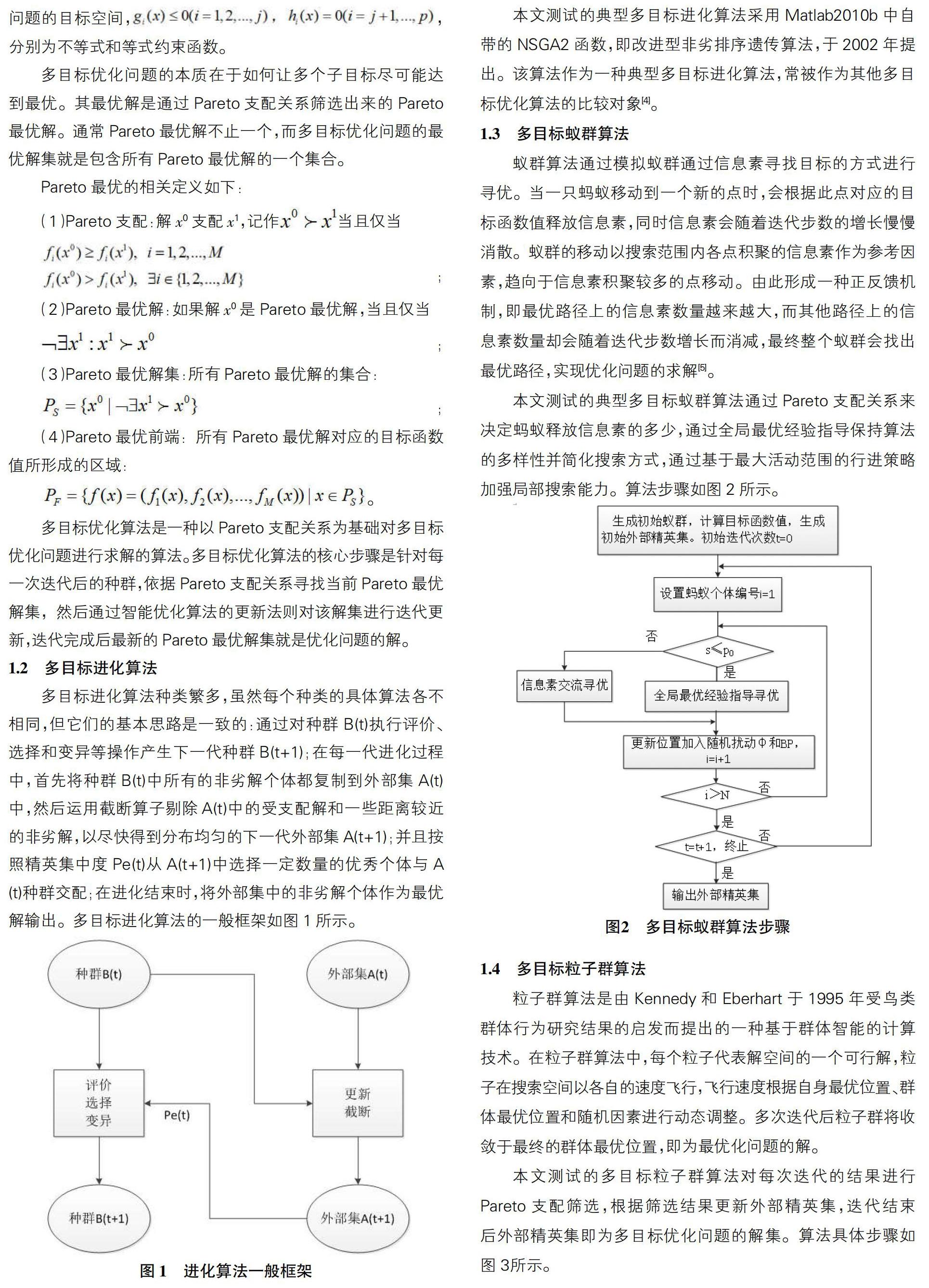
本文测试的典型多目标蚁群算法通过Pareto支配关系来决定蚂蚁释放信息素的多少,通过全局最优经验指导保持算法的多样性并简化搜索方式,通过基于最大活动范围的行进策略加强局部搜索能力。算法步骤如图2所示。
1.4 多目标粒子群算法
粒子群算法是由Kennedy和Eberhart于1995年受鸟类群体行为研究结果的启发而提出的一种基于群体智能的计算技术。在粒子群算法中,每个粒子代表解空间的一个可行解,粒子在搜索空间以各自的速度飞行,飞行速度根据自身最优位置、群体最优位置和随机因素进行动态调整。多次迭代后粒子群将收敛于最终的群体最优位置,即为最优化问题的解。
本文测试的多目标粒子群算法对每次迭代的结果进行Pareto支配筛选,根据筛选结果更新外部精英集,迭代结束后外部精英集即为多目标优化问题的解集。算法具体步骤如图3所示。
2 多目标优化算法的评价指标
多目标优化算法的目标是快速搜索逼近真实Pareto最优前端并且在其上均匀分布,因此评价一个多目标进化算法的性能可以从4个方面去考虑[6]:
(1)收敛性:评价所求Pareto最优解集到真实Pareto最优前端的趋近程度。
(2)分布性:评价所求Pareto最优解集在目标空间分布的均匀程度。
(3)覆盖性:评价两组Pareto最优解相互支配的程度。
(4)搜索速度:评价算法求解优化问题的速度。
Zitzter等人[7]对多目标优化评估指标进行了分类研究。本课题中选择了4个目前常用的评估指标,具体为距离指标[8]GD、分布性指标[9]SP、覆盖指标[7]C和运行时间t。
2.1 距离指标GD
