基于PHM的高速铁路牵引电机滚动轴承健康状态预测
2020-07-30牛齐明张奕黄
牛齐明,刘 峰,张奕黄
(1. 北京交通大学 计算机与信息技术学院, 北京 100044; 2. 河北大学 计算机教学部, 河北 保定 071002; 3. 北京交通大学 电气工程学院, 北京 100044)
采用PHM技术对高速铁路(以下简称“高铁”)装备展开健康状态预测,可以改进目前高铁的维修和管理体制,还能辅助设备安全可靠地运行。在装备的健康状态预测中,从原始传感器的监测数据中提取特征并进行合理的转换,建立高铁装备健康指标,然后通过相关的模型进行预测。由得出的健康指标值,管理人员可以判断装备的健康状态变化趋势,或者所处全寿命某个阶段,从而进行合理地设备管理和维修。准确地预测是PHM健康管理的基础和前提,应该对其进行深入的研究[1-2]。
描述装备健康状态的关键之一是其健康特征的合理选取。为了全面反映装备的状态,许多研究中提取的特征都是高维的,这使得后续计算量增大,计算效率不高[3-5]。如郭亮等[5]从轴承振动信号中抽取了19个特征,为提高计算效率需要用降维方法进行数据处理。由于高铁装备的许多特征是非线性的,PCA和线性判别法等线性降维方法对数据的处理效果不好,因此采用非线性降维方法更合理。非线性降维方法有多维尺度法、等距映射法、马氏距离累积法和自编码器等。多维尺度法是将多维数据简化到低维数据,并使得由降维所引起的任何变形最小的数据分析方法。等距映射法是使用测地距离代替欧几里德距离,并进行多维尺度计算。马氏距离累积法[6]是先进行马氏距离计算,然后对马氏距离特征值进行累加操作。自编码器能从无标签的大数据中自动学习,进行维数约简[7-10]或得到在数据中的有效特征[11-13]。
另一方面,如果模型选取不合理还会造成预测精度的降低。本文选取支持向量机[14]和最小二乘支持向量机[15]作为健康状态预测的对比模型。首先,基于高铁牵引电机滚动轴承健康状态的时间属性,构建了输入数据和输出数据的时间滞后关系;进而,用时滞支持向量机模型和时滞最小二乘支持向量机模型,建立深度堆叠去噪自编码累积健康指标和马氏距离累积指标,进行在线健康状态的连续预测;通过对平均绝对误差、均方根误差和皮尔逊相关系数3个预测指标的分析,可知DSDAE和TDLSSVM方案在高铁滚动轴承健康状态预测的优越性。
1 健康状态预测模型
1.1 振动数据的特征提取
随着高铁牵引电机滚动轴承的使用,振动信号的频率会有所变化,这时仅靠时域特征分析,难以判断其频率的详细构成。小波包是时频特征提取的一种常用方法[16-17]。通过小波包分析和后期处理,能得到振动信号在不同频域上的能量分布图。小波包的优点是,能够更精细地对信号进行分析,尤其能对高频部分进行准确分析,并且能自适应选择与振动信号频谱相匹配的频带[18]。
为优化后续预测模型的预测结果
( 1 )
式中:y为归一化后的数值;ymax为归一化后的最大值;ymin为归一化后的最小值;xmax为小波包变换后能量特征值中的最大值;xmin为小波包变换后能量特征值中的最小值;x为小波包变换后的能量特征值。
用式( 1 )对8个小波包特征进行了归一化[6],见图1。
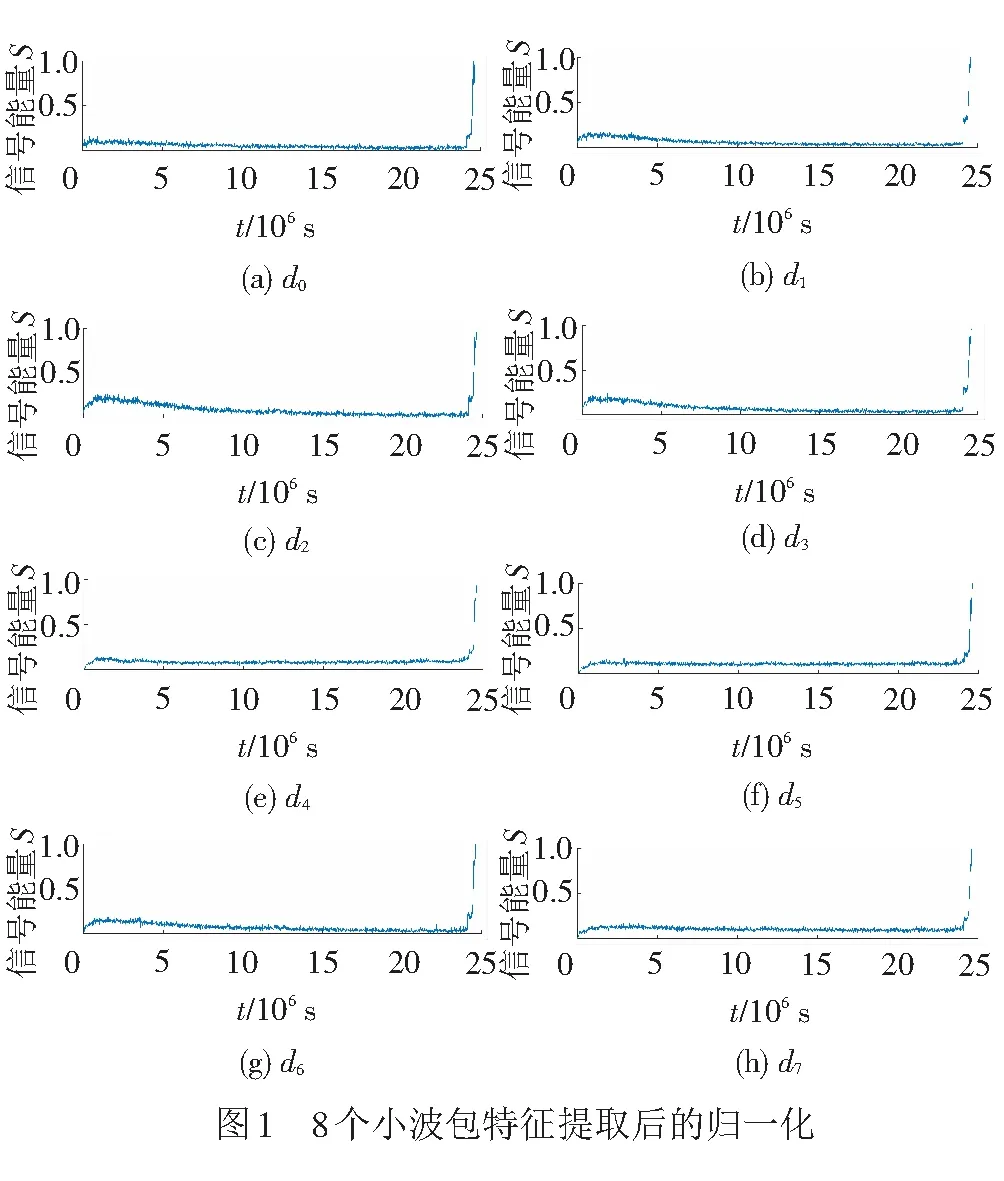
1.2 自编码器累积法
自编码器是学习输入数据表示的一种人工神经网络,它可以作为降维的一种方法来使用。自编码器可以通过训练网络来减小信号中的噪声。在神经结构上,自编码器是一种前馈神经网络,它包含输入层、隐藏层和输出层。从输入层到隐藏层的变换称为编码,从隐藏层到输出层的变换称为解码。这两个变换可以分别定义为两种映射φ、φ。对于单层的自编码器,两种映射分别为
( 2 )
式中:x为输入;c为编码的输出;σ1为编码的激活函数;W1为编码的权重;b1为编码的偏置;y为解码的输出;σ2为解码的激活函数;W2为解码的权重;b2为解码的偏置。
由于输入数据没有标签信息,可知自编码器是一种无监督学习的方法。自编码器的参数通过某种方法如随机梯度下降法来最小化设定的损失函数
L(x,y)=‖x-y‖2
( 3 )
将自编码器扩展就会得到深度自编码器。深度自编码器与自编码器不同之处在于隐层的数目上,深度自编码器有更多的隐层,通过增加隐层数目避免了传统神经网络结构容易陷入局部极小值的问题。深度堆叠去噪自编码器是对输入信号加入噪声,再送入自编码器中使其尽量重建一个与未加噪声输入相同的输出,这种方法可以学到一个更鲁棒性的特征表示。
累积法是Page[19]提出的一种控制图模型。累积法用不断累积待测值与标准值的差值,实现放大数据变化的目的。因此用累积法能够更加敏感地检验微小的变化。对振动数据用深度堆叠去噪自编码器的编码输出值进行累积,通过累积序列值来表示高铁装备健康状态的退化情况。为优化后面预测模型的计算,对累积序列值进行归一化,得到深度堆叠去噪自编码器累积健康指标。这个指标值越大表示装备的健康状态越差,当指标达到1时表示装备完全损坏。
1.3 时滞最小二乘支持向量机
为了能够进行连续预测,需要重构一种时间滞后关系。假设信号序列是{x1,x2,…,xn},用大小为m的窗口重建序列,可以得到多维时间滞后矩阵X和预测向量Y分别为
( 4 )
( 5 )
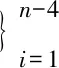
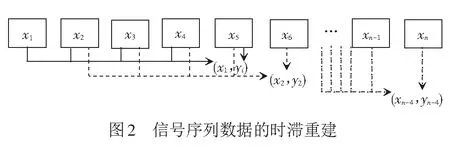
最小二乘支持向量机(LSSVM)是SVM的一种改进方法。LSSVM用等式约束代替了SVM中的不等式约束,方便了Lagrange乘子α的求解,并把误差平方和损失函数作为目标函数。这样通过求解线性方程组问题,提高了求解速度,降低了求解难度。时滞最小二乘支持向量机是具有输入时滞数据和输出预测循环映射关系的最小二乘支持向量机。输入时滞数据集可以表示为X={xi,i=1,2,…,∞}。最小二乘支持向量机模型可以描述为
yk=wTφ(xk)+b+ekk=1,…,N
( 6 )
式中:J为损失函数;w为权值系数向量;γ为可以调节的惩罚系数;k为权向量;ek为误差变量;φ(·)为映射函数;b为偏置。
用Lagrange乘数法可得
L(w,b,e,α)=J(w,e)-
( 7 )
根据KKT条件对式( 7 )求偏导,可得
( 8 )
定义核函数k(xk,yk)=φT(xk)φ(yk),从式( 8 )中消去ek和w后化简,可得
( 9 )
式中:In为化简后的n阶单位矩阵。
从式( 9 )中解得α和b,得到LSSVM模型为
(10)
式中:xk为多维输入;f为一维输出。在最小二乘支持向量机模型中,xk对应时滞最小二乘支持向量机模型时滞数据集中的xi。
2 健康状态预测流程
基于DSDAE和TDLSSVM的高铁牵引电机滚动轴承健康状态预测的流程见图3。
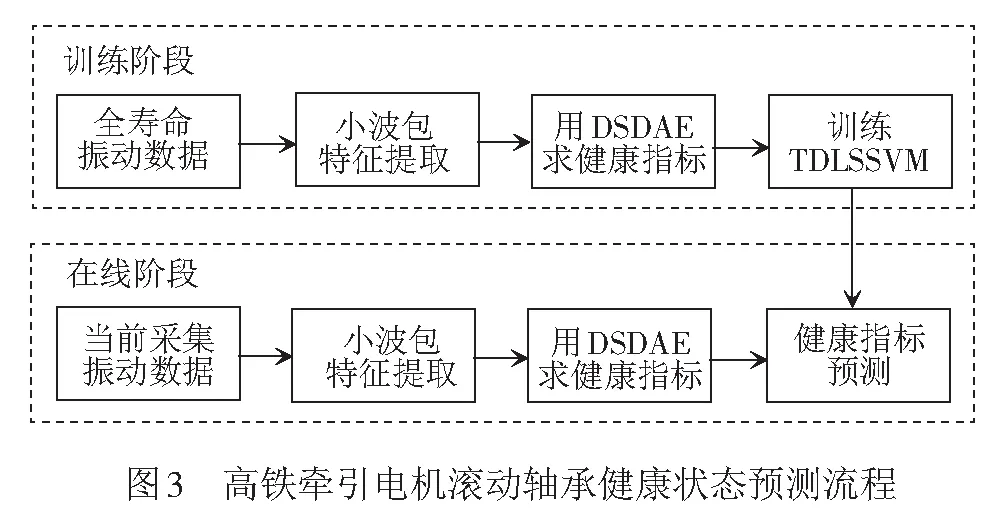
(1) 训练阶段:① 获取高铁牵引电机滚动轴承全寿命振动数据,并通过三层小波包分解进行特征提取;② 应用DSDAE求健康指标,获取牵引电机滚动轴承健康指标;③ 训练TDLSSVM模型。
(2) 在线阶段:①获取准实时振动数据,用三层小波包进行特征提取;②应用DSDAE获取牵引电机滚动轴承当前健康指标;③把当前健康指标输入到训练好的TDLSSVM模型,得到健康指标的预测值。
3 实验和分析
利用美国西储大学PRONOSTIA[20]和基于北京交通大学轴承实验台的工业数据集进行实验。数据由两个实验台传感器获得,轴承试验台见图4。

PRONOSTIA实验台外观见图4(a),可用来测试和验证轴承故障检测、故障诊断和故障预测方法。它由加载、旋转和测量三部分组成。平台提供了真实的球轴承全周期使用寿命振动和温度实验数据。从PRONOSTIA实验台相关传感器获得的振动和温度信号,分别保存在ASCⅡ文件中。振动信号由水平振动信号和垂直振动信号组成。采样频率为25.6 kHz。每10 s采集一次数据,每次采集的时长为0.1 s,则可得到含有2 560个样本的一个记录。每个记录都存储在一个ASCⅡ文件中。对于每个ASCⅡ文件,振动传感器获得的数据包括水平方向振动数据和垂直方向振动数据。此外,相应的振动时间也存储在ASCⅡ文件中。
北京交通大学高速牵引电机轴承试验台NTN又称实验台,其外观见图4(b)。按照功能可以划分为基座部分、轴承部分、驱动部分、控制部分、辅助部分和监测部分,各部分功能简述如下。
基座部分主要由本体和各机械部件所构成,基座上有电机、轴承和油系统等。轴承部分由轴承套筒和内部用于固定轴承的部件组成,用于安装被试验轴承。驱动部分由电机和相应的传动机构构成,用来提供滚动轴承旋转的转速和转矩。控制部分由操作盘、控制电磁阀、传感器等组成,这些部件放在一个控制柜中,用于试验过程中对系统的控制和监测等。辅助部分由供油系统、冷却系统和除雾机等辅助部件构成。检测部分由数据记录仪、振动分析仪、工控机和相应的传感器构成,可用于轴承振动、温度等数据的采集和分析。所有采集的振动数据都存储在数据库文件中。这是具有世界先进水平、目前国内唯一用于高铁的高速牵引电机轴承实验台,可以做高速动车组牵引电机轴承试验。根据实际使用状况,进行不同转速、轴向和径向载荷、温度、润滑油脂等综合条件下的试验,包括急加速试验、温升特性试验和耐久性试验,为高速电动车组的安全运营速度提供基础实验数据。
验证用的数据集来自PRONOSTIA球轴承的垂直振动流数据和工业球轴承垂直振动流数据。球轴承1~5在PRONOSTIA实验床上运行6 h 50 min,共采集了2 463组数据。高速某型号列车中使用的滚动轴承是6311型的球轴承。在实验台上采用加速度传感器对6311球轴承进行了实验,采集其运行信息。采集设备的采样数率为100 kHz。每600 s采集一次数据,每次采集的时长为0.1 s,则可得到含有10 000个样本的一个记录。实验轴承运行时间累计在实验台上6 144 h40 min,共采集36 868组数据。
小波包分解最重要的是基小波的选取,目前常用的小波基有db系列小波、mexh小波和coif小波等。本文实验中根据误差最小化原则,选择哈尔小波进行3层分解来提取数据特征。
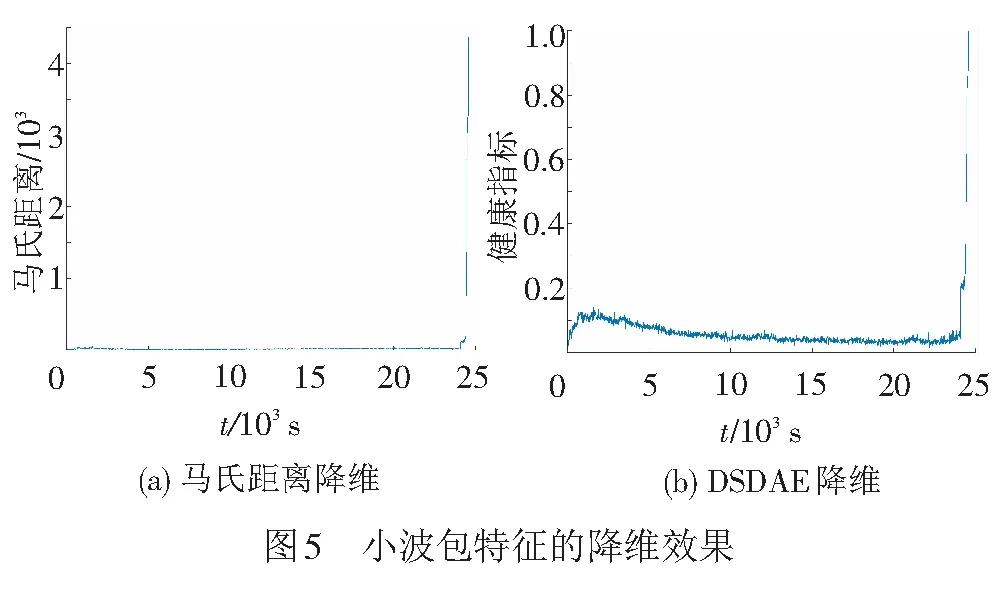
由于所得特征维度较高不便于后面的预测处理,因此用马氏距离和深度堆叠去噪自编码方法对高维特征进行降维。深度堆叠去噪自编码器的隐藏层数是4层,各层的神经元数目分别是25、7、2、1个。PRONOSTIA球轴承降维效果见图5。由图5可见,降维后数据波动大且趋势不明显。
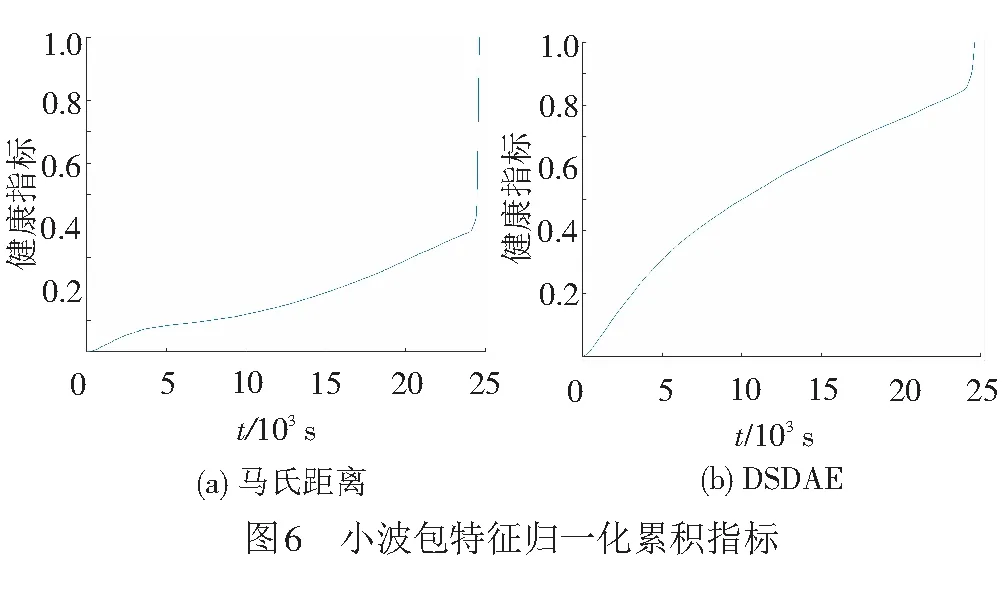
为了解决这些问题,对图5的数据使用归一化和累积法可得到图6。由图6可见,可以看到消除了波动且呈现单调增趋势。
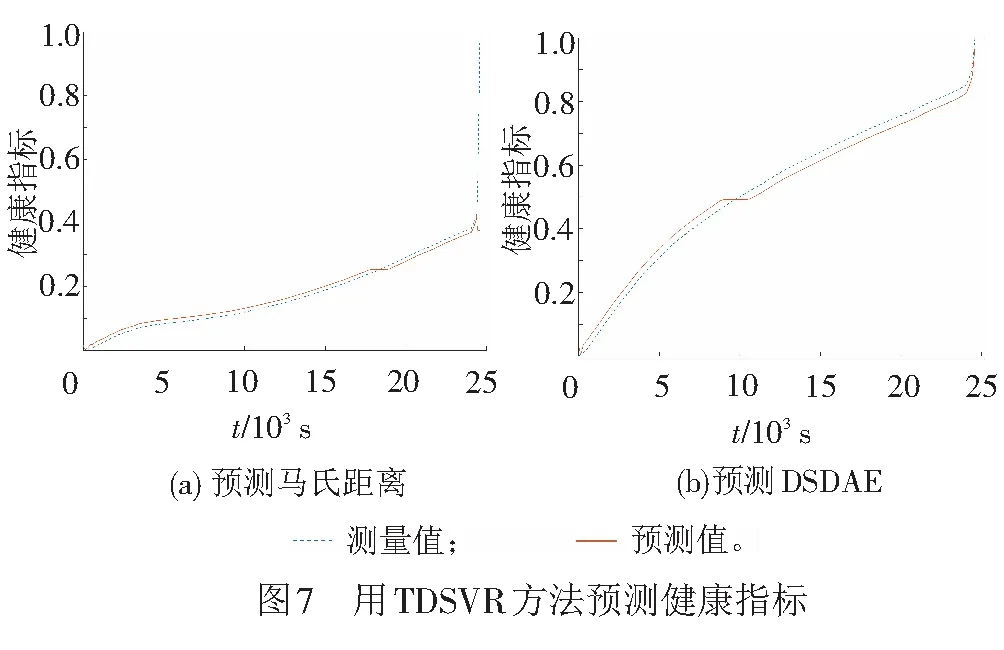
为了说明实验效果,进行了4组实验。窗口大小采用平均互信息法来选取。采用留一法划分训练集和测试集。用80%的样本作为训练集,20%的样本作为测试集。前两组实验是用TDSVR方法预测马氏距离累积指标和DSDAE累积指标。预测结果对比见图7。由图7可见,测量值和预测值的误差比较大,尤其在最后的预测部分预测趋势有误。
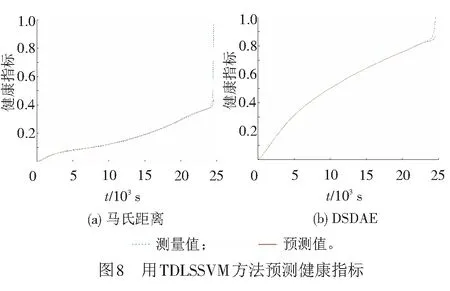
后两组实验是用TDLSSVM方法预测马氏距离累积指标和DSDAE累积指标。预测结果对比见图8。由图8可见,测量值和预测值的误差比较小,均比图7两个子图误差也小,而且在最后的预测部分预测趋势一致。
为了对DSDAE+TDSVR、MDCUSUM+TDSVR、DSDAE+TDLSSVM、MDCUSUM+TDLSSVM这4种方案预测效果进行量化对比,使用了均值绝对误差MAE、均方根误差RMSE和皮尔逊相关系数R这3个指标。
均值绝对误差MAE是绝对误差的平均值,反映预测值误差的实际情况。
(11)
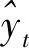
均方根误差RMSE是预测值与观测值偏差的平方和与预测次数比值的平方根,反映预测值与观测值之间的偏差。
(12)
较小的RMSE值意味着预测值和观测值之间的误差变化较小,RMSE反映了预测值偏离观测值的程度。
皮尔逊相关系数两组数据之间线性相关的程度为

(13)
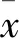
R值介于-1和1之间,R= -1时,两个变量为完全负相关;R=0时,两个变量为线性无关;R=1时,两个变量为完全正相关。总之,相关系数的绝对值越大,相关性越强;相关系数越接近于0,相关度越弱。
模型方面,LSSVM的核函数采用高斯径向基核函数。利用留一交叉验证法对LSSVM预测模型进行了优化,确定最优模型参数。测量值和预测值的计算汇总结果见表1。对比相关数据发现DSDAE+TDLSSVM方案效果最好。其中DSDAE+TDLSSVM方案的MAE指标是0.002 2,RMSE指标是0.006 9,R为0.999 6。
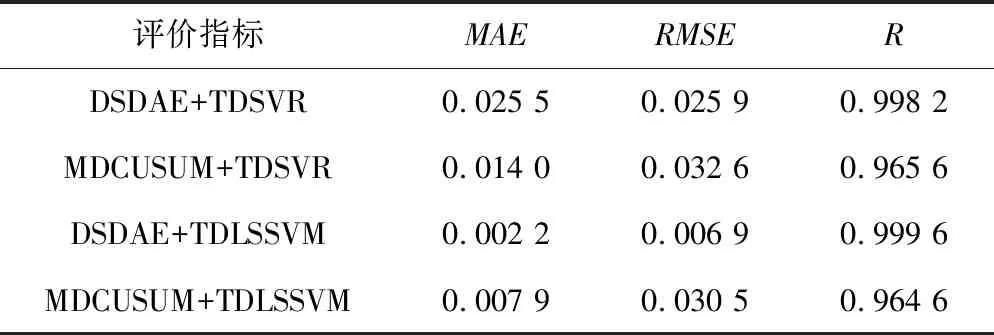
表1 各种方案的总体多指标评分
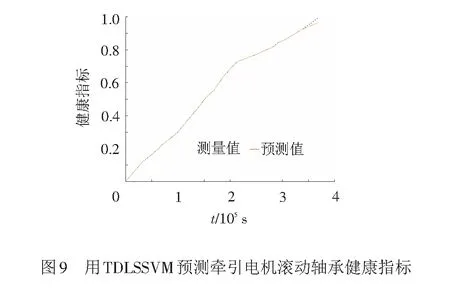
合作实验室高速牵引电机轴承实验台6311轴承全寿命数据的深度堆叠去噪自编码累积归一化健康指标和用TDLSSVM预测健康指标的对比见图9。由于数据比较多,前期的预测值和测量值看上去都重叠在一起,实际两者数值有一定的误差。
高速牵引电机滚动轴承数据集的计算结果见表2。由表2可知,所提方法的泛化能力较强,可以有效地解决高铁装备相关的健康状态预测问题。

表2 DSDAE+TDLSSVM方案的总体多指标评分
4 结论
(1) 本文采用基于深度堆叠去噪自编码器累积和时滞最小二乘支持向量机的滚动轴承寿命预测方案,与其他方案相比更能准确预测基于振动信号的高速牵引电机滚动轴承的剩余使用寿命。
(2) 通过在公开数据集PRONOSTIA和自有高速牵引电机滚动轴承数据集上的实验, 结果表明所提方案对滚动轴承寿命预测有一定的指导意义。
(3) 本文所提方案除了能有效地预测高铁牵引电机滚动轴承的剩余使用寿命, 还可以应用于高铁其它装备剩余使用寿命的预测。
