低空风切变系统建模及其对直升机飞行安全威胁定性分析

2020-07-30赵燕勤陈仁良

航空学报 2020年7期

赵燕勤，陈仁良

南京航空航天大学航空学院直升机旋翼动力学国家级重点实验室，南京 210016

直升机以其独特优越的低空、低速飞行能力，在军用及民用方面均得到了广泛应用，例如海上救援、森林救火、低空巡航监测等。随着直升机可应用领域愈加广阔，已成为航空领域中不可替代的一部分。然而，也正因其低空低速的飞行包线，以及低空任务的广泛多样性，直升机更易遭受低空大气环境影响，从而影响飞行性能甚至威胁飞行安全。通过深入研究大气扰动对飞行器的危害，主要有两种风类型影响飞行器性能：风切变与大气湍流[1]。

风切变是指平均风在一段时间或空间上的变化，湍流是指叠加在平均风上的连续随机脉动。在众风切变形式中，最危险的是水平漩涡一般在600 m高空下的微下击暴流。其具有风速变化多样性、风切变强度变化剧烈的特点，并考虑到直升机的低空低速低能量的飞行特点，微下击暴流对直升机的威胁不容忽视。大气湍流会降低直升机的飞行性能及飞行品质、增加结构载荷振荡，甚至引起驾驶员诱发振荡，增大驾驶难度，影响飞行安全。

微下击暴流作为一种最危险、较简单的空气流动，已有较多成熟的模型建立方案。主要有3种建模方式，其一是建立风场数据库，采用内插法取值，所需数据量大，且难以直观展示风切变特性，不利于定性分析；其二是利用简化的数学模型描述以适用于工程研究的工程化模型[2-3]，主要作为水平距离的函数，风场三维特性不足；其三是根据流体力学和热力学规律建立并求解大气动力学方程[4-5]。结合本文研究目的，选取第3种方法完成风场的建模，生成的风场可较好地体现风场的三维空间变化特性，有利于分析风切变对直升机的本质影响。此外，也可调整建模参数达到不同风切变强度，适应性较强。

为增强风场的不均匀性，进一步分析湍流与风切变的耦合影响，在基础风场上叠加湍流流场。直升机湍流流场的建模也有诸多实现方案。McFarland[6]发展了一种可用于飞行仿真的旋翼叶素紊流仿真(Simulation of Rotor Blade Element Turbulence, SORBET)模型，该模型仅考虑了包含旋翼平面内的二维湍流场，以此为基础，吉洪蕾等[7]进一步发展了新的三维空间湍流流场，本文对该模型所使用的高斯插值算法进行了改进，以研究直升机对大气湍流的响应特性。

目前国内外对固定翼风切变威胁的研究较完善成熟[3,8-9]，且系统地提出威胁因子[10]等定量结论，广泛应用于风切变预警中，此外，Dogan和Kabamba[11]进行了飞机以不同操纵策略飞出微下击暴流的研究，并提出建议的风场逃离策略，以降低坠机事故率。然而风切变对直升机威胁分析的相关文献较少，起步较晚。高华[2]建立了三维组合风切变，并研究了不同方向风切变对直升机的影响，但未考虑风切变量级变化的情况。Liu等[12]分析了在风场不同位置及高度侧向风与垂向风对机体性能的影响，但仅考虑了机体以高速穿越风场的影响，并未考虑涵盖整个飞行包线的飞行速度在风场中的潜在威胁。在文献[4,12-13]中，风切变速度项一般叠加于机体质心处，而未考虑由于风切变相对于机体的转动，或是通过对纵向运动方程求导加入风切变项[14]的方式，不适合于仿真分析，且涉及求导，不利于计算。

本文利用涡环法建立了三维微下击暴流的流场模型，并叠加了可用于实时仿真的三维湍流场。为提高计算精度，捕捉风切变的切变特性，选取特征点建立了含大气扰动的直升机飞行动力学模型，并配备相应的姿态保持增稳控制系统。通过对比分析直升机以不同飞行速度、从不同位置穿越风场的仿真结果，并结合理论推导，得到了直升机状态量变化与风场的关系，总结了含湍流的风切变场对直升机的潜在威胁因素。

1 微下击暴流流场模型

涡环的诱导速度场与微下击暴流风场形式相似，故利用涡环原理可构造微下击暴流风场模型，图1为建模原理示意图，地面上下对称布置强度为Γ的主涡环及镜像涡环，特别的，由于微下击暴流风场的下沉气流并不一定垂直于地面，其外流流谱具有明显的非对称性[1]，涡环面与地面存在倾角。图中,Oxyz为地面坐标系，并分别建立主涡环坐标系OPxyz，其原点OP在O(xP,yP,zP)处；镜像涡环坐标系OLxyz，其原点OL在O(xP,yP,-zP)处；M为参考质点，其坐标为OP(xM,yM,zM)。风场坐标系与地面坐标系相同。

图1 涡环法建模示意图Fig.1 Geometric schematic of ring-vortex model

1.1 涡环诱导速度场计算

为便于分析与计算，在涡环坐标系下计算诱导速度场。首先考虑一般情况，即M点距离涡环较远。设涡环半径为Rv，r1、r2分别为点M距涡环最近及最远的距离值，引入k=(r2-r1)/(r2+r1)，已知当0≤k2≤1时，主涡环的流线方程可用式(1)逼近[2]：

(1)

由流线方程得出涡环在M点处的诱导速度vM的分量分别为

(2)

(3)

(4)

式中：rM为M点距涡环中心轴的距离。

接着，计算涡环中心轴线处的诱导速度。因为此时rM为零，无法通过式(2)～式(4)求解，利用涡环的位函数可推导得，在涡环的中轴线处，水平方向速率为0，垂直方向的速率为

(5)

最后利用Rankine涡原理计算涡丝附近的诱导速度，将涡核看作半径为r的圆环，涡核内部的流速沿半径呈线性分布，而涡核外部仍服从流线方程。

如图2所示，若点M在涡核内部，记点Or为过点OP、M的垂直平面与涡丝的交点，点N为平面与涡环的交点。点N的位置由点M通过定比分点公式求得，即

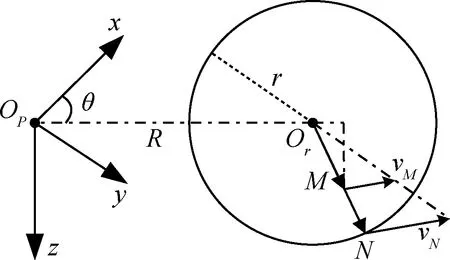
图2 涡核示意图Fig.2 Schematic diagram of vortex core

(6)

因为点N位于涡核的边界处，亦满足流线方程，故根据流线方程可求得点N的诱导速度vN，继而点M的诱导速度vM为

(7)

1.2 地面风场建模

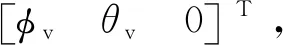
(8)

式中:WMx、WMy、WMz分别为水平风、垂向风、侧向风风速。

1.3 流场建模参数设置及其三维分布

根据联合机场天气研究(Joint Airport Whether Studies, JAWS)计划收集的实际微下击暴流风场强度与空间尺度的统计分析，设置模型的基本参数为：主涡环高度为610 m，涡环半径为915 m，涡核半径r=400 m，中心轴处垂直速率为12 m/s，涡环无倾角。表1为风切变模型参数与高频特征参数范围对比，可看出，所建立的模型参数与一般的风切变特征参数相符。

表1 风切变模型参数与高频特征参数范围对比

涡环中心截面处水平风及垂向风相比风场侧面，风速最大、风切变强度最强，图3为随高度h变化的水平风与垂向风的分布图。由图可得，从上至下，垂向风强度逐渐较小，水平风强度逐渐增大，符合风场变化规律。

图3 不同高度中心截面水平风与垂向风风速剖面Fig.3 Profile of horizontal and vertical wind velocities for various altitudes at central section

接着分析侧向风的变化趋势。图4为300 m高度处，侧向位置y取0～1 800 m时的侧向风风速剖面分布。由图可得，中心截面处的侧向风速度为0 m/s，在y=900 m处侧向风速度最大，速度变化范围为0～10 m/s。

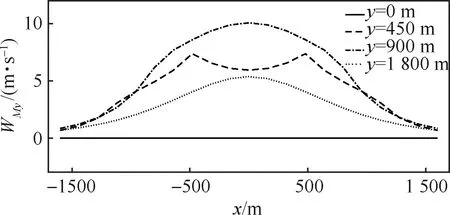
图4 不同方位侧向风风速剖面(h=300 m)Fig.4 Profile of side wind velocity for various orientations (h=300 m)

1.4 风切变风场接口

一般计算旋翼气动力有两种方式:① 仅考虑旋翼桨毂上的大气风速，即假定风速在桨盘上均匀分布；② 利用叶素理论，分别计算旋翼各叶素处含大气扰动的相对来流速度。前者较为简单，但未能充分体现出风切变的切变特性；后者的计算量较大，但计算结果较为精确。

风速在一定范围内变化不大，为充分考虑其切变特性，且在精确建模且不增加计算量的前提下，参考飞机的4点模型[15]，由于直升机旋翼基本覆盖了全机尺度，在旋翼上选取4个特征点计算风切变强度表征全机强度，其示意图见图5。

图5 风切变强度计算示意图Fig.5 Diagram of windshear intensity calculation

(9)

(10)

(11)

式中：各点的气流速度定义于旋翼轴系；Wsaz表示点a处气流速度的z向分量，其他相似符号以此类推；R为旋翼半径。

将旋翼轴系旋转角速度矢量转换至机体轴系可得

(12)

式中：LSB表示旋翼轴系到机体轴系的转换矩阵。

桨毂处的风速WsH由4点的风速度平均求得

(13)

所以，机体相对大气扰动的旋转角速度可等效表示为

(14)

机体平尾、垂尾、机身、尾桨等各部件的风速均由其在地轴系中的位置代入风场模型求得。

2 湍流模型及其三维扩展

根据军用品质规范MIL-F-8785C建立符合平稳随机过程的Dryden紊流模型。利用时间序列数组生成包围机体的三维空间边界，空间内部采用插值算法计算各点湍流速度。

2.1 二维平面大气湍流流场的生成

首先以旋翼所在平面为例说明二维大气湍流流场的生成。如图6 所示，构造一个覆盖整个直升机旋翼平面的长方形，且固定于机体上。长方形短边AB与旋翼桨尖平面相切，且垂直于直升机平飞速度V。长方体的宽度为旋翼直径，长度L大于直升机总长度，并平均分成N段。A、B两点处分别放置一套大气湍流滤波器，每套湍流滤波器根据Dryden模型生成离散大气紊流速度。随着直升机以水平速度V前飞，因为大气紊流相对地面静止，所以生成的大气紊流时间序列UA、UB将按照一定的采样时间分布于两侧边AD、BC上。

矩形长度L可表示为

L=NVΔt

(15)

利用一长度为N的数组记录生成的湍流时间序列，在t=nΔt时刻，其与湍流分段位置的映射关系如图6所示。湍流分段位置k与数组位置m的对应关系为

图6 旋翼面二维湍流场的生成示意图Fig.6 Schematic of two-dimensional turbulent flow field on rotor surface

m=(n+1-k)%N

(16)

式中：“%”为取余符号。

桨叶模型采用叶素分段法，则桨叶i上叶素j在面ABCD中的位置为

xi,j=R+rjcosψi

yi,j=rjsinψi

(17)

式中：rj为桨叶i上叶素j到桨毂轴的径向长度。

由xi,j可以计算得到桨叶气动中心所在横截线与两边交点E、F处的紊流速度分别为UA(mi,j)、UB(mi,j)，且

(18)

应用反距离加权插值(Inverse Distance Weighted)算法计算各叶素气动中心处的大气紊流速率，则

WTi,j=

(19)

图7展示了直升机浸入湍流流场过程中各叶素及近桨尖处叶素的湍流速度变化历程。仿真中各叶素按等圆环面积法分为5段，桨叶片数取为4片。前小段浸入风场阶段，仅桨叶前缘处有湍流速度，随着进一步前飞，各叶素湍流速度分布逐渐扩宽，桨尖处湍流速度较前缘处存在一定的时间延迟，左右两端湍流速度存在明显差异，各桨叶的湍流速度由于使用插值计算，基本在由左右两端曲线包围的范围内变化。

此外，根据图7 可看出，与桨毂处的湍流速度相比，各叶素的紊流速度高频部分明显，实际上，由于旋翼的旋转，使得整个桨盘平面内的紊流速度分布是随机的，各个叶素受到的紊流扰动的高频分量会相互消减。

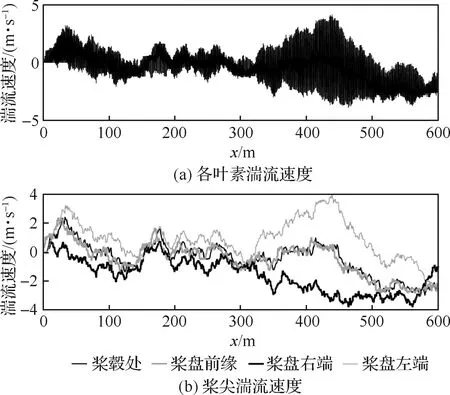
图7 叶素湍流速度与近桨尖处特征点对比Fig.7 Turbulence velocities of elements and rotor hub

2.2 三维扩展

为得到其他部件的湍流流场，依据二维湍流流场将其扩展至三维。在直升机底部构造与旋翼平面ABCD平行的二维湍流生成面MNOP，与旋翼面距离为zH，则两个面共同组成了包围直升机的三维长方体，且类似的，在前端M、N两点放置湍流滤波器。各点气动力计算亦采用反距离加权插值算法，以机身为例说明。

假设机身在湍流坐标系下的位置坐标为[xfyfzf]T，则该部件的湍流速度WTf可由4边的大气紊流时间序列UA、UB、UM、UN表示为

(20)

式中：

(21)

(22)

在含湍流的风切变风场模型中，假设湍流模型与微下击暴流模型相互独立。然而，实验表明，在风切变中，湍流特征长度随风切变的大小与强度以未知的方式增加，所以，本文的湍流强度设为σT=2.1 m/s，表征严重的湍流等级。

3 飞行动力学模型

详细的建模过程可参考文献[16-18]，本文建立了一种单旋翼带尾桨直升机通用的、精度较高的高阶非线性飞行动力学数学模型。旋翼模型采用Pitt-Peters的一阶谐波动态入流模型计算旋翼的诱导速度[19-20]，通过求解挥舞运动学方程[21]计算桨叶挥舞角及挥舞角速率。由各片叶素处的来流速度计算得各叶素的迎角、侧滑角及来流马赫数，对风洞试验数据插值得到翼型的升力系数CL及阻力系数CD，继而可得各片叶素上作用的气动力，最终求得整个旋翼的气动力和气动力矩。机身、平尾、垂尾的相对来流速度均考虑了旋翼下洗、侧洗的影响，并通过风洞试验数据插值得各部件上作用的气动力及气动力矩。采用Bailey模型计算尾桨的拉力和扭矩。

模型运动学方程可表示为

(23)

3.1 模型验证

将飞行力学模型计算得到直升机配平结果与稳态飞行试验数据[22]对比,如图8～图10所示。用于配平的直升机总重为7 257 kg，飞行高度为1 600 m。从图中可以看出，本文计算结果与飞行试验结果吻合良好，误差基本保持在10%之内。小速度下配平计算结果与飞行试验结果相差较大，总距操纵量与需用功率均小于飞行试验数据，主要有两方面因素，一方面为在小速度时保持稳定飞行非常困难，所以飞行试验的误差不可避免；另一方面为本文所采用的动态流入模型不能有效捕捉小速度飞行时的尾迹收缩效应。尾桨操纵量与飞行试验数据保持约5%的误差。

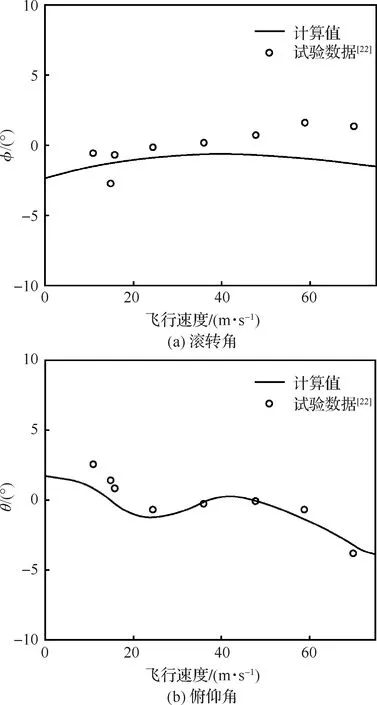
图8 配平姿态角与飞行试验对比Fig.8 Comparison of trim characteristics of attitude angle with flight test

图9 配平操纵杆量特性与飞行试验对比Fig.9 Comparison of trim characteristics of control stick with flight test

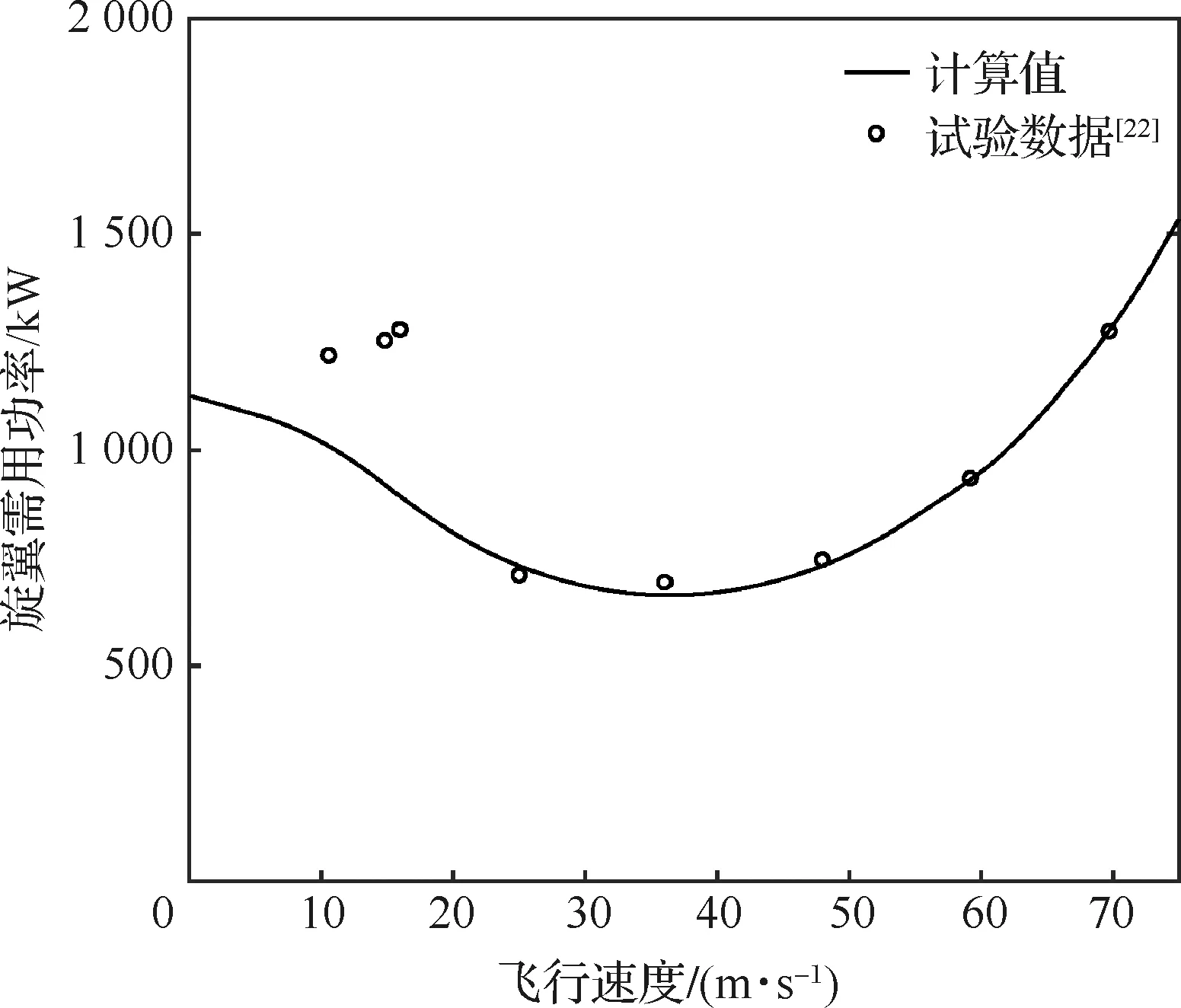
图10 配平旋翼需用功率与飞行试验对比Fig.10 Comparison of trim characteristics of main rotor power required with flight test

综上，可认为本文建立的飞行力学模型满足仿真计算需要。

3.2 增稳控制系统

直升机自身的不稳定性，尤其是在飞越风场时，配备飞行控制增稳系统以改善飞行品质、提高飞行安全显得尤为必要[23]。因此，仅考虑直升机飞过风场时来自风场变化导致的响应威胁，排除机体自身的不稳定性，将具有姿态保持功能的增稳控制系统集成在动力学模型中。

本文采用的飞控系统主要根据文献[16-17]构建。其为样机提供全包线全权限实时控制，包括了4个部分:内环提供角速率阻尼的增稳系统；提供纵向稳定性的俯仰偏置舵机；具有姿态保持及空速保持的飞行航迹稳定系统;能进行初级操纵解耦的混合器。

4 飞行动力学仿真

4.1 无湍流的风切变场

首先进行不同飞行速度的比较，选取3个较为典型的前飞速度V，即20 m/s、40 m/s、60 m/s，分别代表低速飞行、巡航飞行以及高速飞行。以300 m飞行高度从距离风场中心1 800 m 处出发从中心剖面飞越风场。飞越风场的过程中，姿态角变化不大，其中俯仰角变化幅度相对较为明显，如图11所示。其水平、垂直地速以及高度随飞行距离变化的历程曲线如图12所示。由图中可以看出，不同速度的地速变化曲线接近，且与图3中水平风速的变化曲线基本重合，这说明在空速保持控制器的增稳控制下，机体基本可以较好地跟踪风速变化。换言之，直升机优异独特的水平机动性能，使得水平风切变对直升机的影响较小。

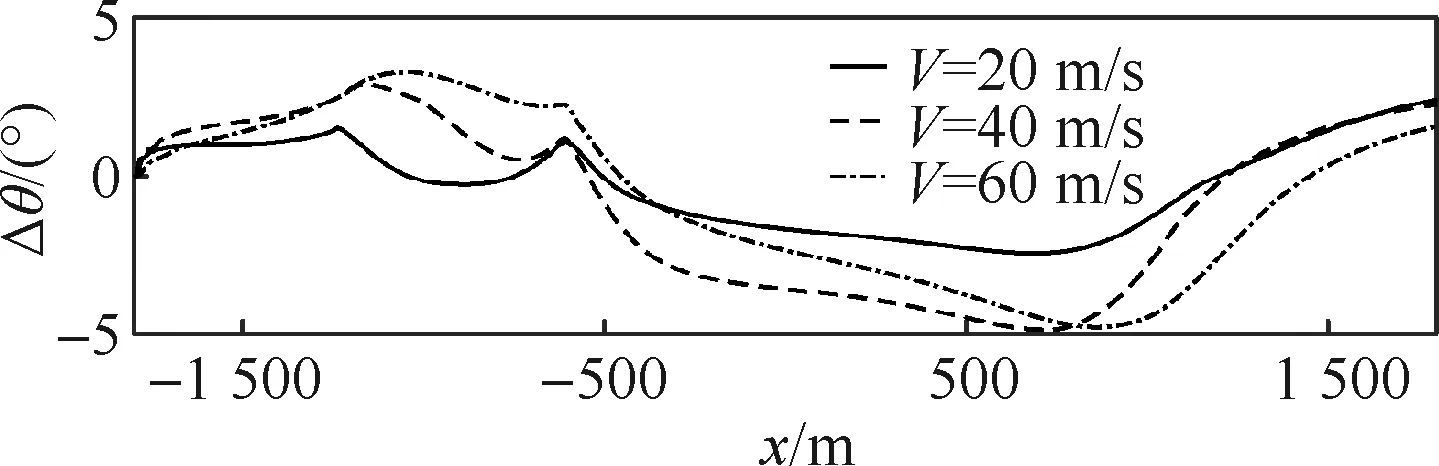
图11 不同速度穿越微下击暴流的姿态角变化历程Fig.11 History of attitude angle change for various velocities through microburst

接着观察图12中垂向速度与高度变化曲线。可以看出，在初期飞行高度变化不大时，不同前飞速度下的垂向速度变化相似，且与下降风风速相似。随着进一步的前飞，高度降低，随之遭遇的垂向风也减弱，因此机体下降速度减缓。此外，小速度飞行时对垂向下降风更敏感，也更易遭遇威胁，主要是因为相同的下降速度下，小速度飞行所需时间更长，导致下降高度更大。因此，从高度变化上看，随前飞速度增大，高度变化减小。

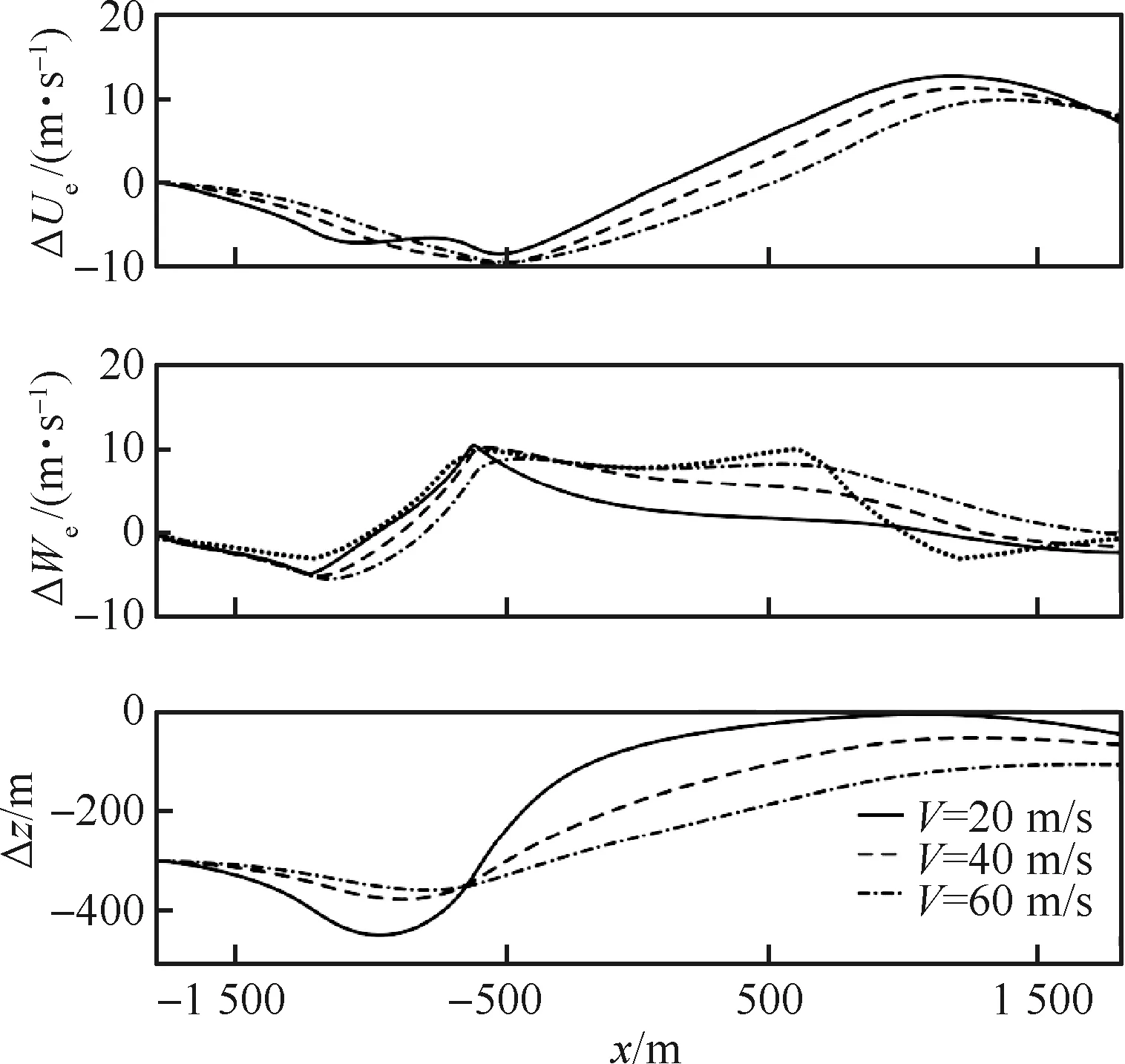
图12 不同速度穿越微下击暴流的地速及高度变化历程Fig.12 History of ground speed and height change for various velocities through microburst

为进行不同飞行高度的比较，选取了3个较为典型的高度h，即150 m、300 m、450 m，分别代表水平风较弱而垂向风较强、水平风及垂向风均衡以及垂向风较强而水平风较弱的飞行条件。直升机以40 m/s的平飞速度飞越风场中心，各主要状态量变化如图13、图14所示。从图13中可看出，水平风主要影响俯仰角，但俯仰角变化幅度正常，其余姿态角变化幅度更小，不予赘述。地速变化幅度在初期由于高度相差较大，因此区别较明显，随着进一步飞行，高度差异缩小，地速变化趋于一致。类似的，在高度更高的位置，垂向下降速度越大，但综合不同高度飞行的高度变化历程可以看出，高度越高，虽然遭遇更大速度下降气流，但是最终飞出风场时仍处于较高位置，换言之，在遭遇风切变时，较高的高度更安全。

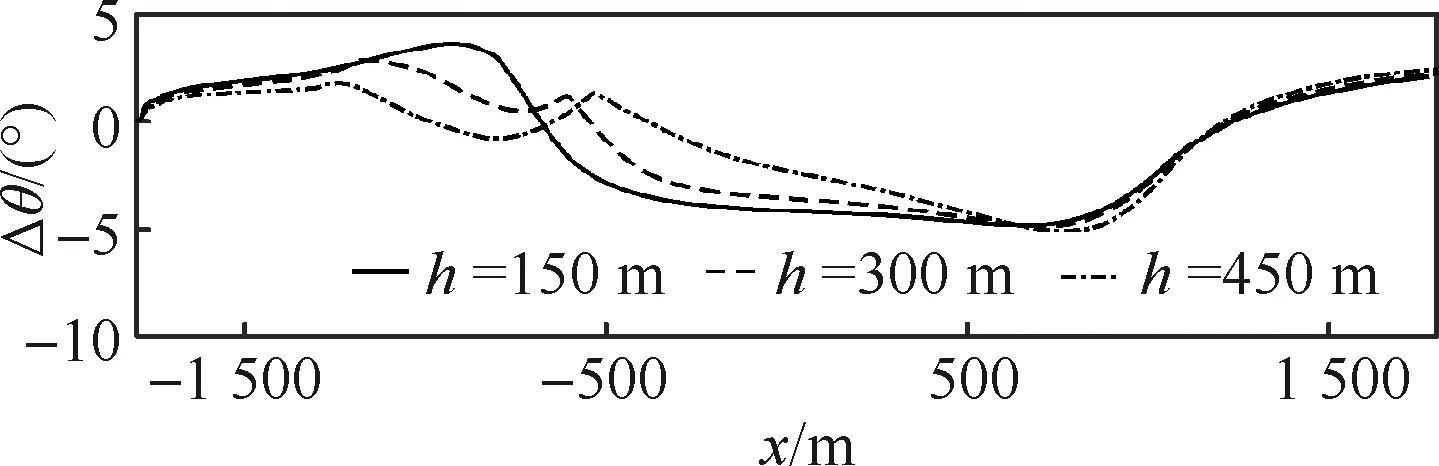
图13 不同高度穿越微下击暴流的姿态角变化历程Fig.13 History of attitude angle change for various altitudes through microburst

图14 不同高度穿越微下击暴流的地速及高度变化历程Fig.14 History of ground speed and height change for various altitudes and height through microburst

最后是不同飞行侧方位的比较，结合图4选取了3个较为典型的方位，即y=±900 m、y=0 m。y=±900 m处为左右侧向风最大侧向位置处，主要验证机体对不同方向侧向来流的对称性，以及侧向风的威胁程度。y=0 m处无侧向风作为对照基准组。机体飞行速度为40 m/s，飞行高度为300 m。

偏航角及地速变化历程如图15和图16所示。在侧向风较大的区域，由于距离风场中心较远，水平风及垂向风影响显著减弱，侧向风占主导地位，因此，姿态角中偏航角变化最明显，其变化历程如图15所示。由图可看出，机体的航向稳定性较好，且随侧方位变化呈现出显著的对称性。图16为地速变化曲线，与中心截面变化历程相比，水平及垂向地速变化显著减小，威胁降低；侧向运动速度变化范围小，且由于直升机的航向稳定性作用，侧向风影响基本可控。

图15 不同方位穿越微下击暴流的姿态角变化历程Fig.15 History of attitude angle change for various orientations through microburst

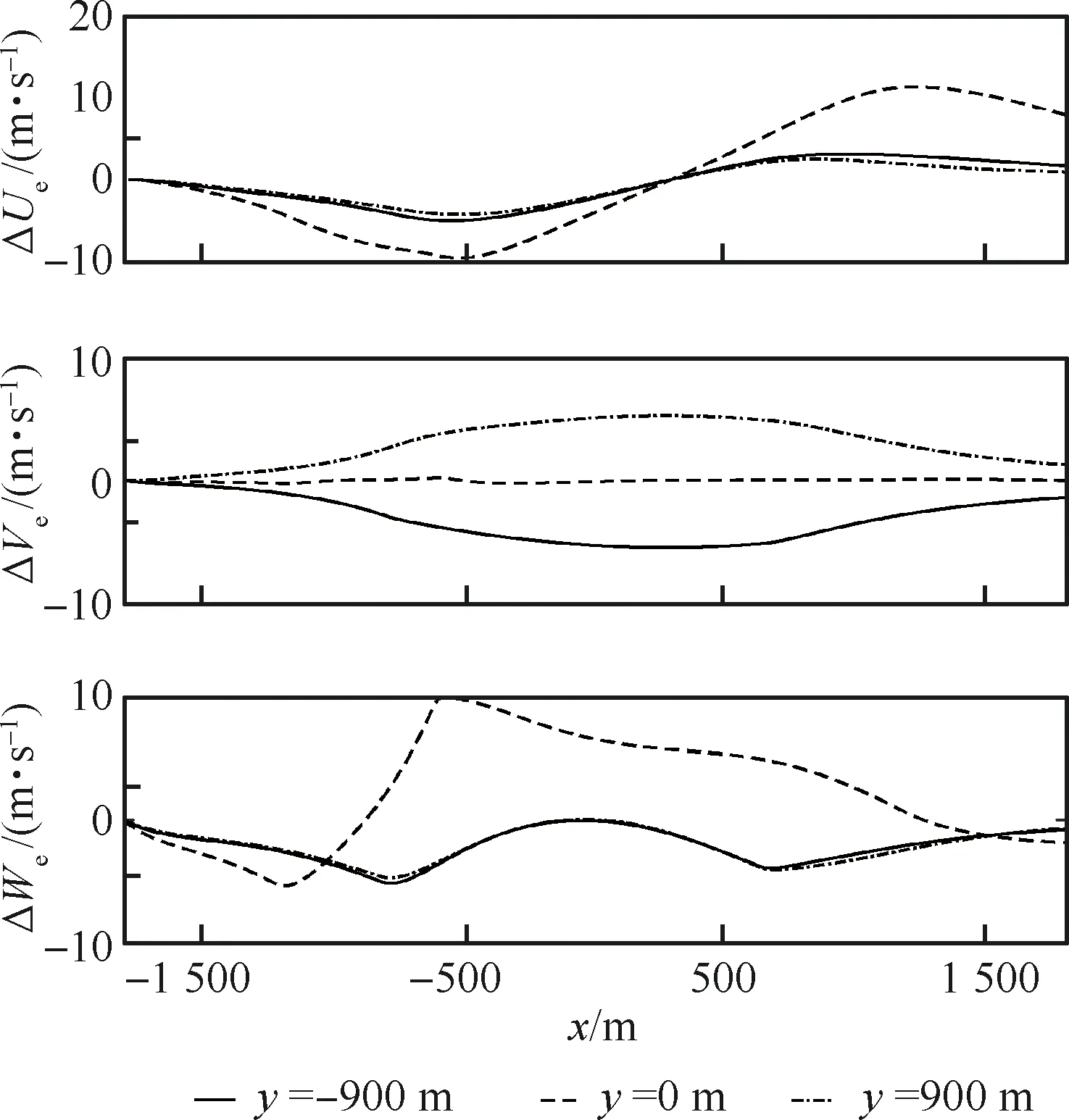
图16 不同方位穿越微下击暴流的地速历程Fig.16 History of ground speed change for various orientations through microburst

所以，若遭遇微下击暴流，应向远离风场中心，垂向风更小的区域进行规避，可有效降低风场威胁。

4.2 飞行器运动与风场关系推导

本节结根据直升机的动力学方程，推导含有风速及风切变项的运动学方程，从宏观理论角度，解释验证由仿真推测出的直升机状态量变化与风场的关系。

则由动力学方程可得

(24)

式中：A表示气动力项；g表示重力项。

在上文的仿真中，由于姿态保持增稳控制器的作用，水平及横向的气动力项变化与操纵有关，且纵横向耦合强，解耦困难;另一方面，由上述仿真结果可看出，机体可跟踪横纵向风速变化，不是引起威胁的主要因素。

相反的，垂向风与其他通道耦合较小，未配备垂向通道保持的增稳控制器，机体响应体现了在裸机状态下直升机受垂向风的影响。此外，由上文仿真可推出，垂向风对机体的威胁占主导作用，因此有必要着重分析垂向通道的动力学方程。

将式(24)展开后可得

Vaz+paVax-qaVay=gcosθwcosφw-La/m+

Waz+paWax-qaWay

(25)

式中：升力项可表示为

(26)

忽略横纵向操纵量对拉力系数CT的影响，则CT可表示为总距杆量与垂向空速的函数[24]，即

(27)

记：

(28)

考虑到姿态保持器可保证机体姿态角变化量在正常平衡范围内小幅波动，故ωa×Va、ωa×Wa项可看作小量，暂时忽略其影响。

式(25)化简并移项后可得

(29)

式(29)可看作一元非齐次线性常微分方程。求解得(Vaz-Waz)关于时间的变化函数：

(30)

式中：Pcoef与初始状态量有关。

在上文的仿真中，直升机以水平飞行的配平状态飞入风场，则此时的配平状态可表示为

Vaz=Waz=0 m/s

T≈mgcosθwcosφw

(31)

若总距θ0保持定值，代入式(28)可得

Pconst=0

(32)

设初始时刻遭遇的垂向风大小为Waz0，则

Vaz(t)=-Waz 0e-Pvariat+Waz(t)

(33)

由式(33)可知：机体垂向运动速度在经历短暂的过渡后，与当前位置处的垂向风速保持一致。

从合作用力平衡角度分析，当机体垂向运动速度与垂向风速相等时，垂向空速为0，与初始配平状态相同，此时，机体在气流轴系下作平飞运动，与4.1节仿真得到的结论相符。

同理，该分析方法也可用于纵横向通道的计算及验证。

4.3 叠加湍流的风切变场

上文分析在无湍流的情况下，风切变对直升机的影响特性，由于实际的风场中必有湍流场存在，且湍流可降低飞行器飞行性能，甚至影响飞行安全，因此有必要验证湍流与风切变场共同作用的影响，分析两者是否会由于耦合作用产生更严重的威胁。

通过仿真得到的含湍流的风切变的主要状态量变化如图17所示。飞行条件为：直升机以40 m/s 的平飞速度从300 m 高度、距离中心点1 800 m 处从中心剖面飞越含湍流的微下击暴流风场。图17中展示了3条曲线的变化历程,观察仅由湍流作用的曲线变化，发现其主要激励姿态角小幅高频震荡，但基本在平衡点附近。类似的，垂向速度变化的震荡亦体现出高频的效果，而水平风速的变化则由于积分作用表现更为平缓。图中的插值拟合曲线为将同样飞行条件下，通过仿真得到的微下击暴流与湍流分别作用的时间历程曲线按相同水平位移做插值拟合并合并得到的曲线。比较该条拟合曲线与仿真得到的变化历程，可发现两者较为重合，这说明湍流与风切变的影响相互独立，无明显耦合，换言之，湍流主要影响直升机小幅短期高频的姿态角等变化，而宏观的风切变则主要诱导机体速度、高度等状态量的大幅低频变化。