N位二进制-BCD转换电路VHDL设计
2020-07-28廖超平
廖超平


摘 要:该文以16位二进制数为例,分析了N位二进制-BCD转换算法,并以此算法为根据,应用VHDL语言设计了一种实现N位二进制-BCD转换的电路。该设计的基本循环是将二进制码表示中各个数码往左边移动一位,最高一位二进制位的数码移出二进制表示进入最低一位十进制位的8421表示中,而每个十进制位的8421表示中权为8的位的数码都移到高1位十进制位的8421表示中重新组合成新的8421表示。
关键词:二进制-BCD转换 VHDL 移位
中图分类号:TP303 文献标识码:A 文章编号:1672-3791(2020)06(a)-0065-03
在非常多的数字系统的设计中,存在数据输入,用户习惯使用十进制(BCD)码形式,而数字系统内部则使用二进制。所以,在使用VHDL设计数字系统时多位二进制-BCD转换电路是经常使用的。多位二进制-BCD转换电路在各种智能仪表、电子秤和数控机床等数字系统的设计中广泛使用。
1 N位二进制-BCD转换算法分析
下面以十六位二进制数字的二进制- BCD 转换为例分析多位二进制- BCD转换算法。十六位二进制数字的二进制码表示的一般表达式如下:
下面算式中,最右边的2的幂每降一次表示移动一次数字。
上面分两种情况,原因是为了保证下一次移位后,符合十进制数进位和十进制数的表达形式,即:每位十进制数码应该只能是0~9这10个数码。
在X03=0时,(A03,A02,A01,A00)是(0,0,0,0)~(0,1,0,0)这几个值,向左边移动一位后,没有对高一位的进位,而且本位最大变成(1,0,0,A-4),符合十进制的表达形式。
在X03=1时,(A03,A02,A01,A00)是(0,1,0,1)~(1,0,0,1)向左边移动一位后,最少也是(1,0,1,A-4),存在对高一位的进位,进位是逢十进一,所以要进行修正。修正的方法就是A0加三变成X0后再移位。
以后每次移位都遵守同样的规律,移动16次后,即完成转换过程。
2 N位二进制-BCD转换电路原理框图
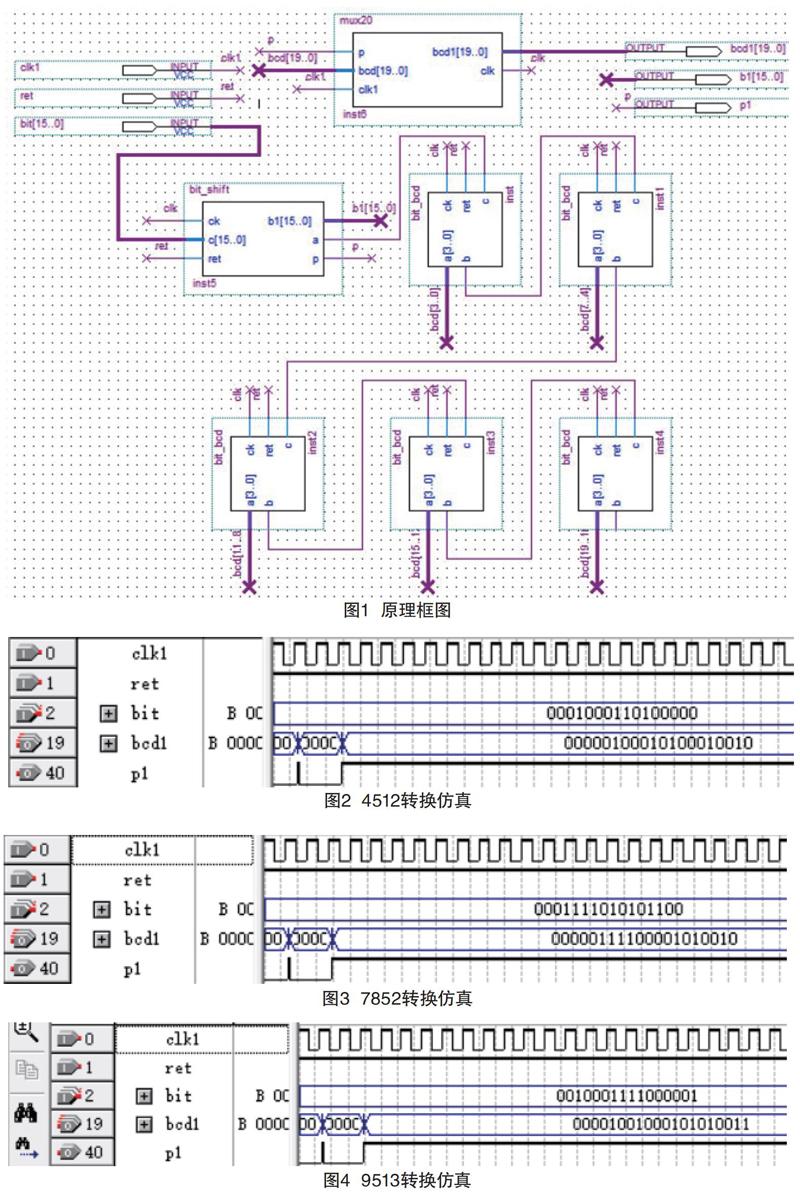
以16位二进制数字为例,N位二进制-BCD转换电路原理框图如图1所示。
bit[15..0]是16位二进制的bit输入,clk1是移位时钟,ret为复位,共有5个bit-BCD单元。每个单元负责一位BCD数码的移位和加3或加0操作。转换过程是先复位,并行输入16位二进制数的bit码。然后,奇次时钟到来时5个单元各自进行加3或加0,偶次时钟到来时移位。经过了32个时钟、16次移位完成整个转换过程。
3 bit-bcd单元VHDL代码
LIBRARY ieee;
USE ieee.std_logic_1164.ALL;
ENTITY bit_bcd IS
PORT ( ck : IN STD_LOGIC;
ret : IN STD_LOGIC;
c : IN STD_LOGIC;
a : OUT STD_LOGIC_VECTOR(3 DOWNTO 0);
b : OUT STD_LOGIC ) ;
END bit_bcd;
ARCHITECTURE one OF bit_bcd IS
signal t : std_logic;
signal q ,c1,c2: std_logic_vector(3 downto 0);
BEGIN
b <= c1(3); a <= c1;
PROCESS( ck,ret )
BEGIN
if ret = '0' then
t <= '0';
elsif ck'event and ck = '1' then
t <= not t;
end if;
END PROCESS ;
PROCESS( ck,ret,c )
BEGIN
if ret = '0' then
c1<= "0000";
elsif ck'event and ck = '1' then
if t='1' then
c1(0)<=c;c1(1)<=c1(0);c1(2)<=c1(1);c1(3)<=c1(2);
else c1<=c2;
end if;
end if;
END PROCESS ;
PROCESS( c1 )
BEGIN
CASE c1 IS
WHEN"0000"=> c2<="0000";--0011
WHEN"0001"=> c2<="0001";--0100
WHEN"0010"=> c2<="0010";--0101
WHEN"0011"=> c2<="0011";--0110
WHEN "0100" => c2 <= "0100" ;--0111
WHEN "0101" => c2 <= "1000" ;--1000
WHEN "0110" => c2 <= "1001" ;--1001
WHEN "0111" => c2 <= "1010" ;--1010
WHEN "1000" => c2 <= "1011" ;--1011
WHEN "1001" => c2 <= "1100" ;--1100
WHEN OTHERS => c2 <= "0000" ;--0000
END CASE ;
END PROCESS ;
END ;
4 仿真結果
该设计用Quartus II仿真,功能正确。典型仿真结果见图2~图4。
在图2中,00010001101000/00转换成4512。
在图3中,0001111010101100转换成7852。
在图4中,0010001111000001转换成9513。
参考文献
[1] 王迎春,吉利久.一种基于简单移位的二—十进制相互转换算法[J].电子学报,2003(2):221-224.
[2] 潘吴,钟珞,陈杰.单片机十六进制数与BCD码转换新探讨[J].微机发展,1997(6):35-36.
[3] 高皑琼.基于EDA技术的数字频率计[J].计算机产品与流通,2018(8):58.
