Blow-Up Solution of the 3D Viscous Incompressible MHD System

YANG Xin-Guang,SHI Wei and LU Yongjin

1 Department of Mathematics and Information Science,Henan Normal University,Xinxiang 453007,China.

2 Department of Mathematics and Economics,Virginia State University,Petersburg,VA 23806,USA.

Abstract.The 3D viscous incompressible magneto-hydrodynamic(MHD)system comprised by the 3D incompressible viscous Navier-Stokes equation couples with Maxwell equation.The global well-posedness of the coupled system is still an open problem.In this paper,we study the Cauchy problem of this coupled system and establish some logarithmical type of blow-up criterion for smooth solution in Lorentz spaces.

Key Words:MHD equations;blow-up criteria;Lorentz space.

1 Introduction

The 3D viscous incompressible magneto-hydrodynamic(MHD)system describes the magnetic properties of electrically conducting fluids. It is a strongly coupled PDE system that combines the Navier-Stokes equation of fluid dynamics together with Maxwell’s equations of electro-magnetism. Many problems related to the individual component of the coupled system remain open.For example,the well-posedness of in 3D for the Navier-Stokes equation,that describes the motion of classical fluid flow,is listed as one of the Millennium problem by the Clay Mathematics Institute.Therefore,the global wellposedness for the MHD system in 3D is also open problem.In this paper,we want to study blow-up criterion for smooth solution to the Cauchy problem of the MHD system in 3D where the underlying fluid is viscous and incompressible.The coupled system in the variables ofuandbis given as the following

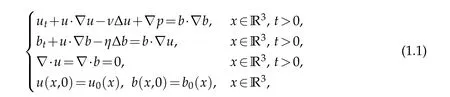
whereu=(u1,u2,u3)∈R3denotes the velocity field,b=(b1,b2,b3)∈R3is the magnetic field,p∈R is the scalar pressure,ν＞0 is the viscosity,η＞0 is the magnetic diffusivity,u0andb0are the initial velocity field and magnetic field satisfying ∇·u0=0 and ∇·b0=0 in the distributional sense.

For system(1.1),there are many results available in the literature pertaining to the well-posedness and regularity of the global solution. For instance,the famous Beale-Kato-Majda criterion[1]gives conditions to the well-posedness of a global smooth solution of(1.1)when the magnet fieldbis a constant andν=0.In this case,(1.1)reduces to the classical incompressible Euler equation and the BKM criterion describes the control of vorticity for the fluidω=curluinL1(0,T;L∞).For more details,one can refer to Majda and Bertozzi[2]. If the magnet fieldbis a constant,then(1.1)reduces to the classical incompressible Navier-Stokes equation,of which many blow-up results for smooth solutions in terms of pressure or the velocity field are available.One could refer to Serrin[3],Zhou[4–6],Fan,et al.[7],Chae and Lee[8],Zhou and Lei[9],Cao and Titi[10],Kato and Ponce[11],Breselli and Galdi[12],Lemarié-Rieusse[13]and references therein.

Since the global well-posedness of the 3D Navier-Stokes equation is unknown,the solution of MHD flow should not have more regularity than that of Navier-Stokes equation.The global well-posedness of the 3D MHD equations,including the regularity criteria for the strong and weak solutions,have also drawn a lot of attentions. We review some of the blow-up criterion of smooth solutions in terms of the velocity field or pressure:in[14],Cao and Wu gave two regularity criteria of strong solutions in Sobolev spaces;He and Xin in[15]derived a regularity criterion of the velocity field for the weak solutions;Gala[16]investigated the blow-up criteria in multiplier spaces.For more interesting results,we may refer to Chen,et al.[17],Fan,et al.[7],Jia and Zhou[18],Zhou[19]and literature therein.

As far as we know,there are no results in the literature that are concerned about blow-up criterions for smooth solution to(1.1)inLorentz spaceof logarithmical type.This is our main motivation for this article.The Lorentz spacesLp,q(see detailed definition in Section 2)are generalization of theLp-spaces and the norm of a function in a Lorentz space provides control in the spread of a measurable function in both the horizontal and vertical directions by rescaling the measure in both the range and the domain of the function.Thus,our results are generalization of similar results in theLpspace for the Navier-Stokes equation and MHD equation.We compare these results in more details in Section 2 below(see Remark 2.1).The rest of the paper will be organized as follows:we review some preliminaries and state the main results in Section 2,the proof of which is then given in Section 3.

2 Preliminaries and main results

Throughout this article,we use the following notations:we denote the Lebesgue space byLp(R3);the standard Sobolev spaces byHm(R3)(m∈R)equipped with the norm

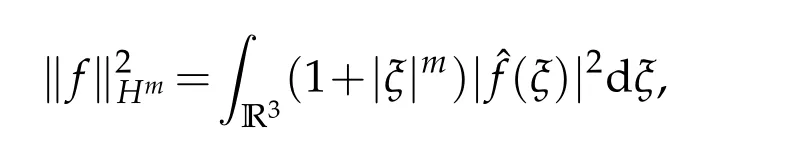
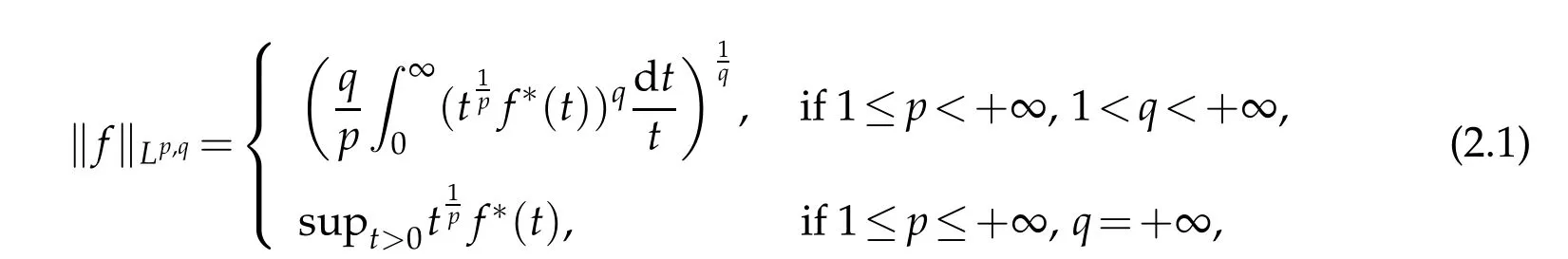
wheref*is the decreasing rearrangement offdefined asf*(t)=inf{s＞0:μ(|f|＞s)≤t}fort＞0.

In particular,ifp=q,the Lorentz spaceLp,pis the LebesgueLpspace.Ifq=+∞,we writewhich is also called the weakLpspace.

The above definition implies the following continuous embeddings:

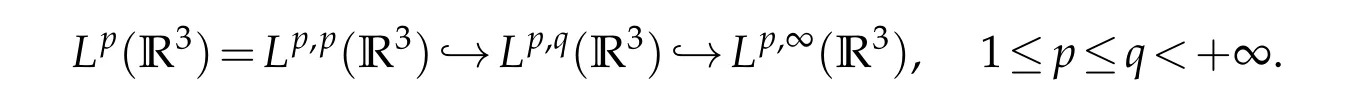
The purpose of this paper is to establish the two blow-up criterions for smooth solutions,one based on the fluid velocity field and the other based on the gradient of fluid velocity field in terms of Lorentz spaces.

Theorem 2.1.(Blow-up Criterion for Fluid Velocity Field)Assume that the initial data(u0,b0)∈H1(R3)satisfying divergence free conditions∇·u0=0,∇·b0=0.Let(u,b)be a smooth solution to the Cauchy problem(1.1)for0≤t＜T.Then(u,b)is smooth at time t=T provided that the following condition holds

i.e.,

Theorem 2.2.(Blow-up Criterion for Gradient of Fluid Velocity Field)Assume that the initial data(u0,b0)∈H1(R3)satisfying∇·u0=0and∇·b0=0,(u,b)is a smooth solution to the Cauchy problem(1.1)for0≤t＜T.Then(u,b)is smooth at time t=T,provided that the following condition holds

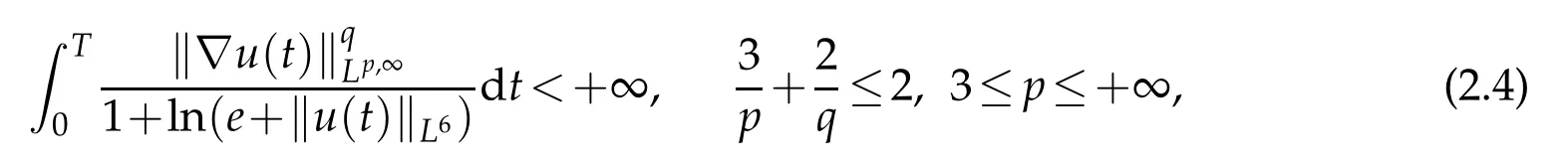
i.e.,

Remark 2.1.Cao and Titi[10],and Jia and Zhou[18]also investigated the Cauchy problem(1.1).In these results,the initial data is assumed to be more regular that what we assume here,to be more specific,(u0,b0)∈Hs(R3)(s≥3)with ∇u0=∇b0=0.Jia and Zhou[18]derived that the solution is smooth ifu3,bi∈Lα(0,T;Lγ(R3))withi=1,2,3 andorare sufficiently small.Cao and Titi[10]proved that the solution is smooth if

While in our paper,we only need the initial data(u0,b0)∈H1(R3)with ∇u0=∇b0=0,and give a regularity criteria in Lorentz spaces in terms of the velocity field or gradient of velocity field,hence our results have extended the results of[10]and[18].

3 Proof of main results

The novelty for the proof of main results is to use the incompressible conditions and construct auxiliary terms based on the following identity

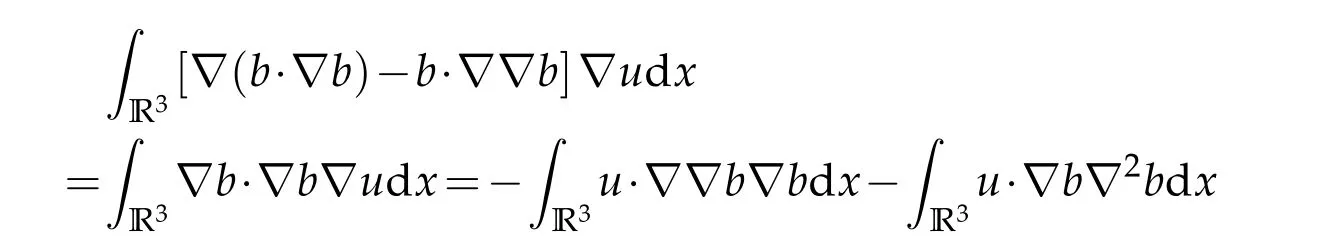
then by virtue of the interpolation inequality in Lorentz spaces,we could conclude our result.

In order to prove Theorems 2.1 and 2.2,we need the following lemma which can be found in[2].

Lemma 3.1.The following inequality holds for any integer m≥1:

We also need the Hölder inequality and the Gagliardo-Nirenberg inequality in Lorentz spaces given as:(see O’Neil[20]or Lorentz[21]))

Lemma 3.2.1 ≤p2,p3≤+∞, 1 ≤q2,q3≤+∞

and the Hölder inequality in Lorentz spaces

holds true for some positive constant C.

Lemma 3.3.Let f∈Lp,q(R3)with1≤p,q,p4,q4,p5,q5≤+∞.Then the Gagliardo-Nirenberg inequality in Lorentz spaces

holds for a positive constant C and

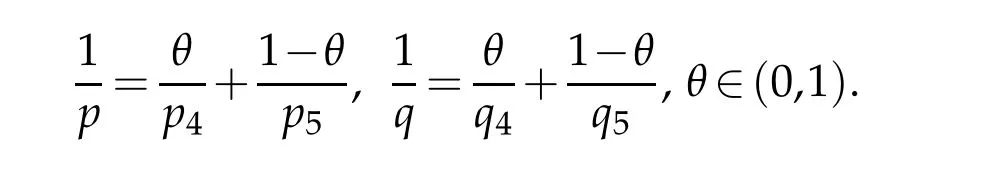
3.1 Proof of Theorem 2.1

Applying ∇to the first equation of(1.1),then taking inner product with ∇uinL2(R3),we get

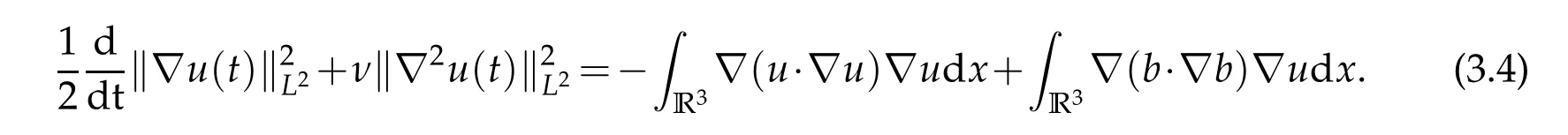
Similarly,applying ∇to second equation of(1.1),then taking inner product with ∇binL2(R3),we obtain

Combining(3.4),(3.5)and using ∇·u=0,∇·b=0,we derive that

Next,we shall estimate every term on the right-hand side of(3.6).

Using the Hölder inequality in Lorentz spaces(see,Lemma 3.2),the Young inequality,we get

where we have used the Gagliardo-Nirenberg inequality in Lorentz spaces(see,Lemma 3.3)to obtain

Similarly,

where we have also used the Gagliardo-Nirenberg inequality in Lorentz spaces forb:

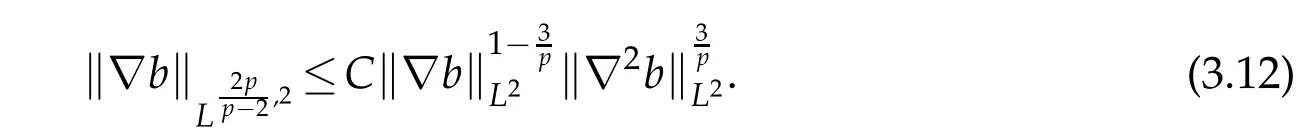
From(3.4),(3.5),(3.7)-(3.11)and the Sobolev embedding theorem,we conclude that

i.e.,

By the Gronwall inequality,we deduce

which gives a finite bound forprovided that

Thus we have completed the proof of Theorem 2.1.

3.2 Proof of Theorem 2.2

We shall estimate every term on the right-hand side of(3.6)by different interpolation inequalities.

Using the Hölder inequality in Lorentz spaces,the Young inequality and Lemma 3.2,we get

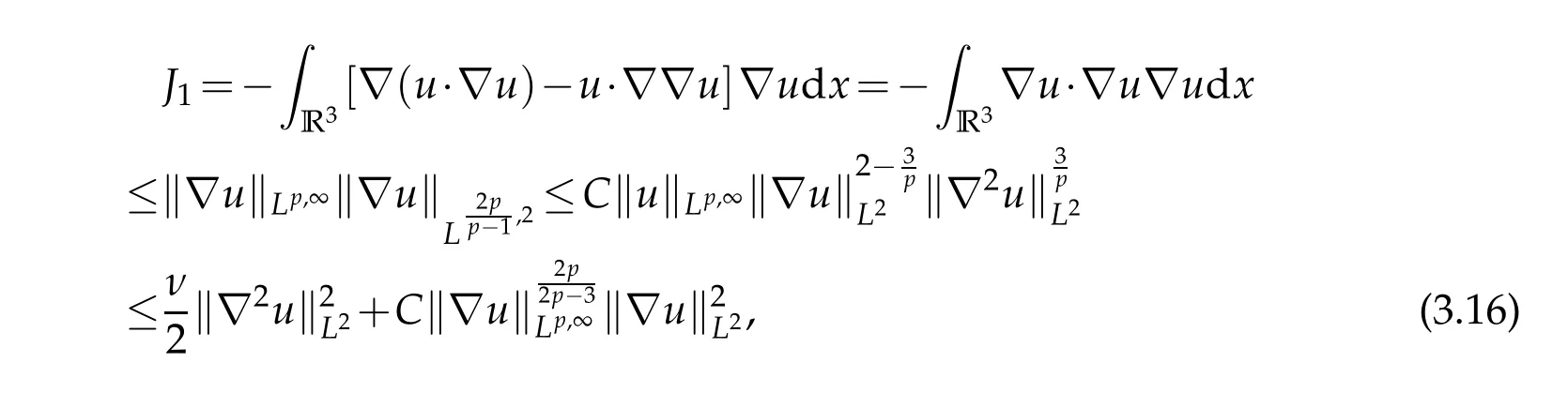
where we have used the Gagliardo-Nirenberg inequality in Lorentz spaces,i.e.,

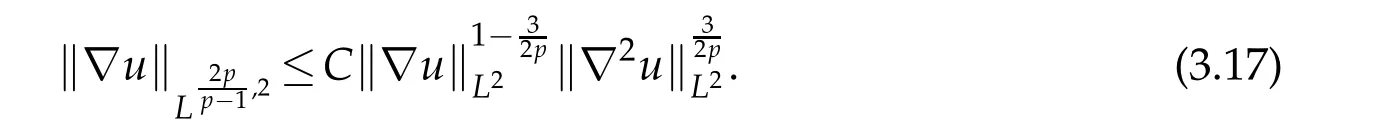
Similarly,

where we have also used the Gagliardo-Nirenberg inequality in Lorentz spaces,i.e.,

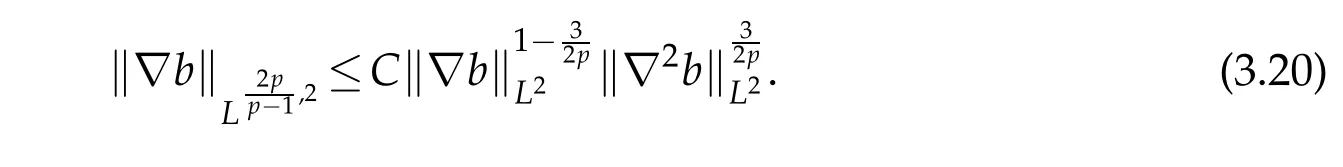
Combining(3.16)-(3.20)and the Sobolev embedding theorem,we conclude that

i.e.,

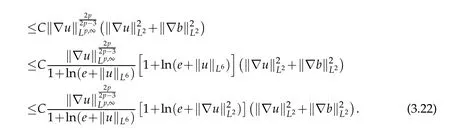
By the Gronwall inequality,we deduce

which gives a finite bound forprovided that

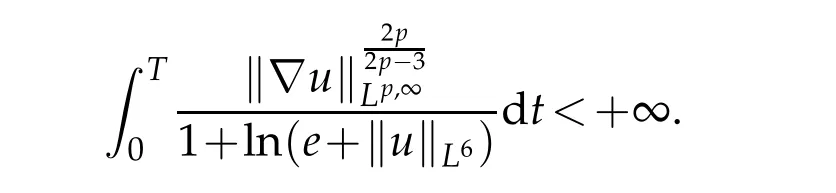
Thus we have completed the proof of Theorem 2.2.

Acknowledgement

Xin-Guang Yang was partially supported by the Fund of Young Backbone Teacher in Henan Province(No.2018GGJS039).Yongjin Lu is partially supported by NSF(Award No:1601127).

The authors thank referees for his/her comments,which led to improvements in the presentation of this paper.