基于神经网络的异步电动机离散容错控制

雷启鑫，于金飞，于金鹏，于海生

(青岛大学 自动化学院，青岛 266071)

0 引 言

近几十年来，科学技术飞速发展，异步电动机的综合性能也随之得到了很大改善，凭借其性能可靠、设计简洁、易于维修等优点，被广泛应用在电动汽车和日常生活中。但异步电动机的驱动系统具有多变量、强耦合、高度非线性等复杂特性，并且存在负载扰动、参数不确定等内外部扰动控制难题[1]。经过众多学者的研究，已经提出了许多先进的控制方法，如反步法[2-4]、滑模控制[5]、反馈线性化[6]、模糊逻辑系统[7-8]、哈密顿控制[9]等。然而，以上控制方法没有考虑电机运行过程中执行器故障造成的影响。

异步电动机控制系统执行器中的核心部件为逆变器，在起着将直流电源逆变为交流电源作用的同时，其过电流保护也避免了因电压、电流过大产生的电机绝缘损坏[10]。逆变器的可靠性关系到整个驱动系统的稳定运行，但由于电力电子器件的脆弱性，恶劣工况、负载扰动和电网扰动等会导致功率开关管被高压击穿或外部击损，损坏功率器件及其控制电路。功率器件故障主要分为功率管开路和短路、功率开关无驱动信号等[11]，其中，功率管开路故障发生时，会使执行器输出电压经逆变器后产生的三相电压出现较大波动，使电动机控制性能下降,甚至对设备及人身安全造成严重的损害。因此，研究一种异步电动机离散容错控制方法，在执行器故障发生时在线补偿，保证位置跟踪性能，对提高异步电动机控制系统的可靠性具有重要意义。

针对交流电动机系统执行器故障，现有文献多采用观测器技术进行故障诊断并结合自适应技术实现容错控制。文献[12]分别设计扩张观测器和滑模观测器，观测双电机同步驱动伺服系统中的负载侧非匹配不确定项并设计决策单元，估计失效因子，通过调整或重构控制律，保证系统的跟踪性能。与文献[12]相比，文献[13]所设计的控制器无需故障检测环节，通过自适应方法直接更新控制参数，对失效故障及时补偿，系统结构更加简单。然而，上述文献所述的控制方法，均基于连续时间的电动机系统设计，无法直接用于异步电动机离散系统。与连续时间控制方法相比，离散控制更易于描述实际问题，因此针对异步电动机系统设计离散容错控制方法，具有更好的稳定性和可实现性[14]。为解决上述问题，本文考虑执行器失效故障和偏差故障，结合动态面技术[15-16]和反步法，并利用自适应神经网络技术[16-18]设计容错控制器。与之前方法相比，本文的离散容错控制方法主要优点有：

(1) 将容错控制应用于异步电动机离散系统，同时考虑执行器失效故障和偏差故障，更适用于实际工程应用；

(2) 利用自适应神经网络技术实现容错控制，减小执行器故障对系统造成的不良影响；

(3) 采用动态面技术，解决了反步法应用到离散系统中产生的“计算复杂性”和“因果矛盾”问题，减轻在线计算负担。

仿真结果表明，该控制方法在故障发生后仍可保证位置跟踪性能，提高了异步电动机控制系统的可靠性。

1 异步电动机离散模型

在同步旋转坐标系d,q下，按转子磁链定向(ψq=0)，异步电动机系统离散模型[18]可表示如下：

(1)

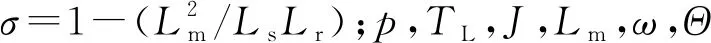
为了简化上述模型，定义新的变量如下：

x1=Θ,x2=ω,x3=iq,x4=ψd,x5=id,

利用上述新定义的符号，同时考虑执行器故障，异步电动机系统离散模型可表示：

(2)

式中：Δt表示系统的采样周期；ρq(k)和ρd(k)为失效因子，且0≤ρq(k)<1，0≤ρd(k)<1；vd(k)和vq(k)为未知但有界的偏差函数。

本文设计控制器的控制目标是在正常和故障状况下均能保证位置跟踪性能，使控制输出x1稳定跟踪跟给定信号x1d。

2 容错控制器设计

根据反步法原理，定义系统误差：

(3)

式中：x1d(k)和x4d(k)为给定的期望信号；定义动态面滤波器：ζi[αid(k+1)-αid(k)]-Δtαid(k)=Δt·αi(k)，αid(0)=αi(0)，i=1,2,3，虚拟控制函数αi(k)经滤波器输出得到αid(k)。

步骤1 据离散故障模型式(2)的第1个方程得：

e1(k+1)=x1(k)+Δtx2(k)-x1d(k+1)

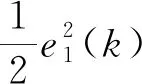
(4)

构造虚拟控制函数α1(k):

(5)

由式(4)和式(5)得：

(6)

步骤2 据离散故障模型式(2)的第2个方程得：

e2(k+1)=x2(k)+a1Δtx3(k)x4(k)+

a2ΔtTL-α1d(k+1)

(7)

构造虚拟控制函数α2(k)：

(8)

在实际异步电动机系统中，所带的负载都是有界的，故假设|TL|≤d，d为正常数。

由式(7)和式(8)得：

(9)

步骤3 根据离散故障模型式(2)的第3个方程得：

e3(k+1)=f3(k)+b5Δt{[1-ρq(k)]uq(k)+vq(k)}

式中：

f3(k)=(1+b1Δt)x3(k)+b2Δtx2(k)x4(k)-

(10)

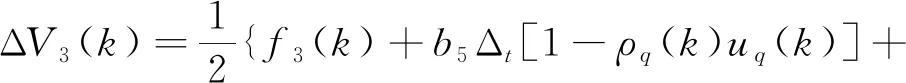
(11)

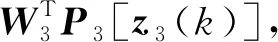
选取控制律与自适应律：

(12)

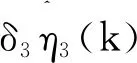
(13)

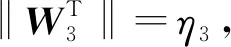
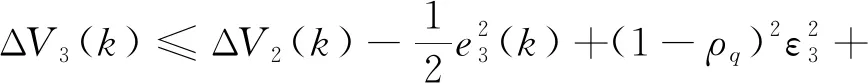
(14)

步骤4 根据离散故障模型式(2)的第4个方程得：

e4(k+1)=(1+c1Δt)x4(k)+b4Δtx5(k)-x4d(k+1)

b4Δtx5(k)-x4d(k+1)]2

(15)

构造虚拟控制函数α3(k)：

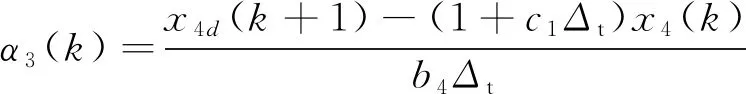
(16)

由式(15)和式(16)得：

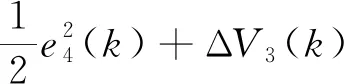
(17)

步骤5 根据离散故障模型式(2)的第5个方程得：

e5(k+1)=f5(k)+b5Δt{[1-ρd(k)]ud(k)+vd(k)}

式中：

f5(k)=(1+b1Δt)x5(k)+b3Δtx2(k)x3(k)+

(18)

(19)

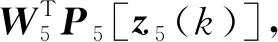
选取控制律和自适应律：

(20)

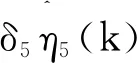
(21)

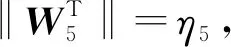
(22)

3 稳定性分析

定义μi(k)=αid(k)-αi(k)，i=1,2,3,选取Lyapunov函数：

(23)

求V(k)的一阶差分得：

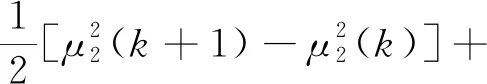
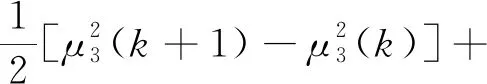
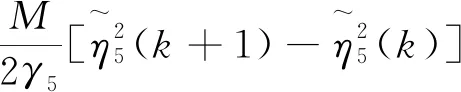
(24)

定义νi(k)=αi(k)-αi(k+1)，由滤波器形式得：

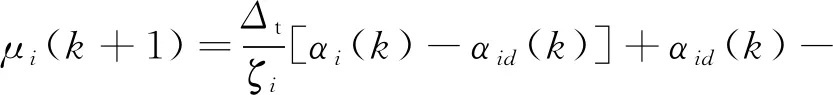
进而得到：

(25)

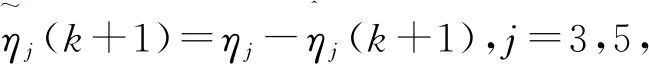
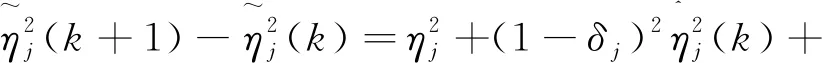
2γj‖Pj(zj(k))‖ej(k+1)ηj-

由杨氏不等式和‖Pj[zj(k)]‖2≤lj，j=3,5，得：

(26)

(27)

(28)

(29)

由式(12)和式(20)得：

(30)

(31)

(32)

(33)

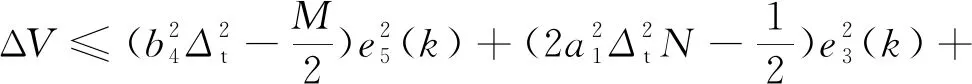
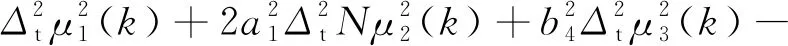
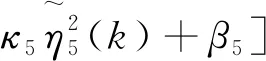
式中：

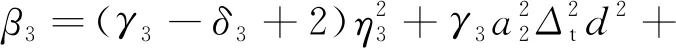
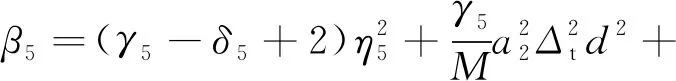
选择合适的P和Δt，使不等式满足：

4 仿真结果分析

为验证本文的离散容错控制方法的有效性，在MATLAB环境下进行仿真分析。控制系统框图如图1所示。异步电动机额定功率为1.1 kW，额定频率为50 Hz，额定转速为750 r/min，电机参数如表1所示。

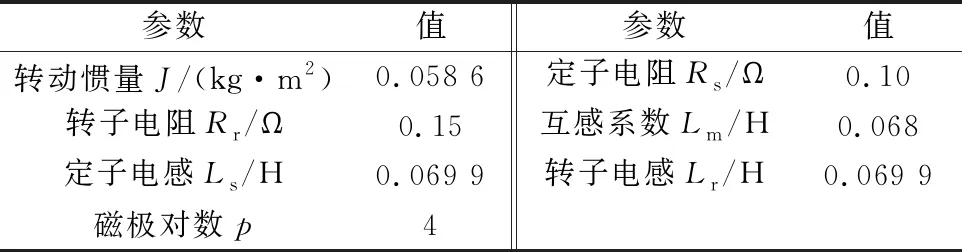
表1 异步电动机模型参数

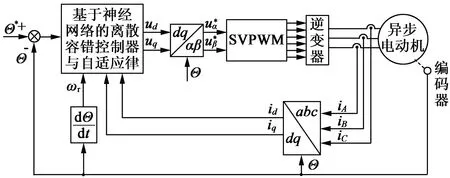
图1 控制系统框图

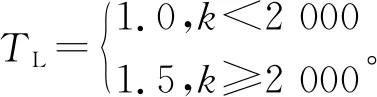
将本文设计的容错控制方法与无容错控制方法进行对比仿真实验。考虑异步电动机控制系统中逆变器开路故障，出现的执行器失效和偏差故障如下。

执行器失效故障：

执行器偏差故障：

控制器参数如表2所示。

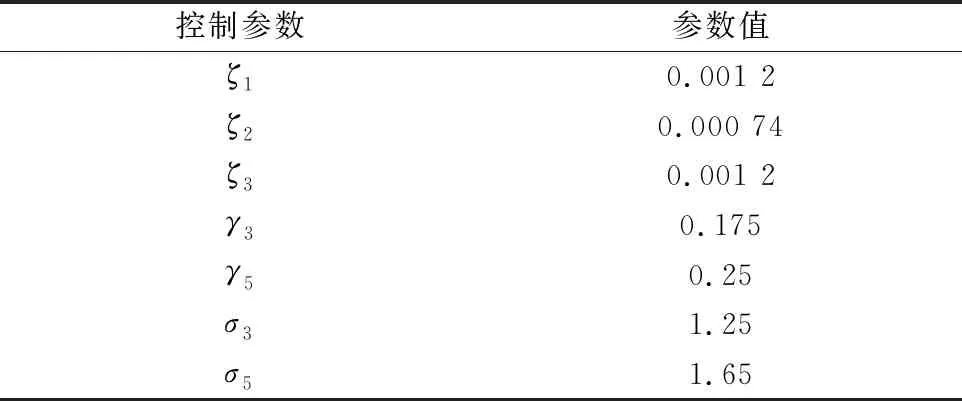
表2 控制器参数

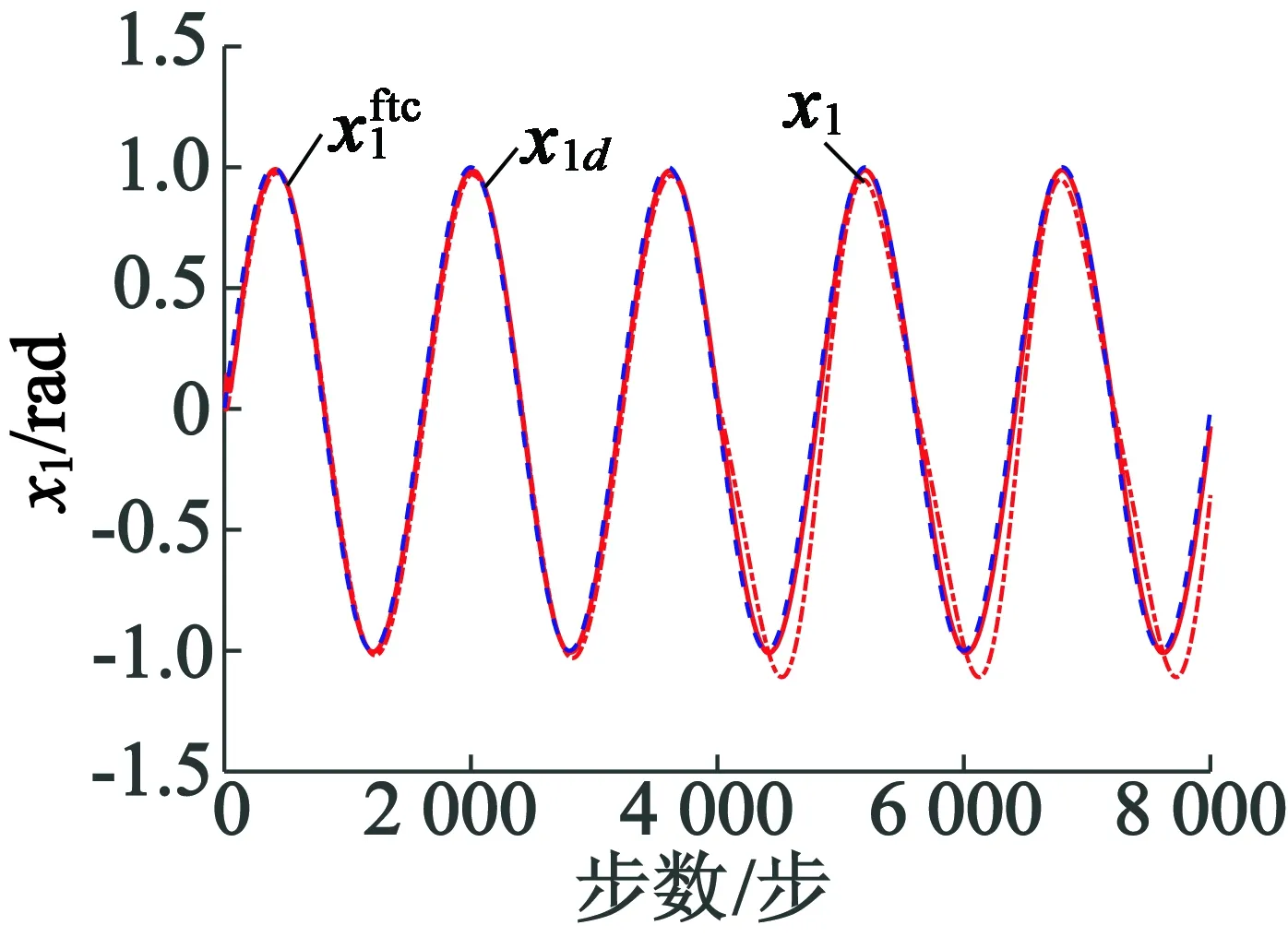
图2 位置跟踪曲线

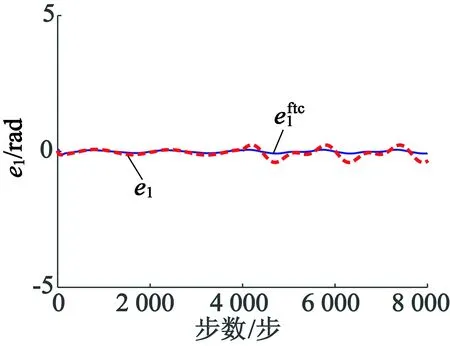
图3 位置跟踪误差曲线

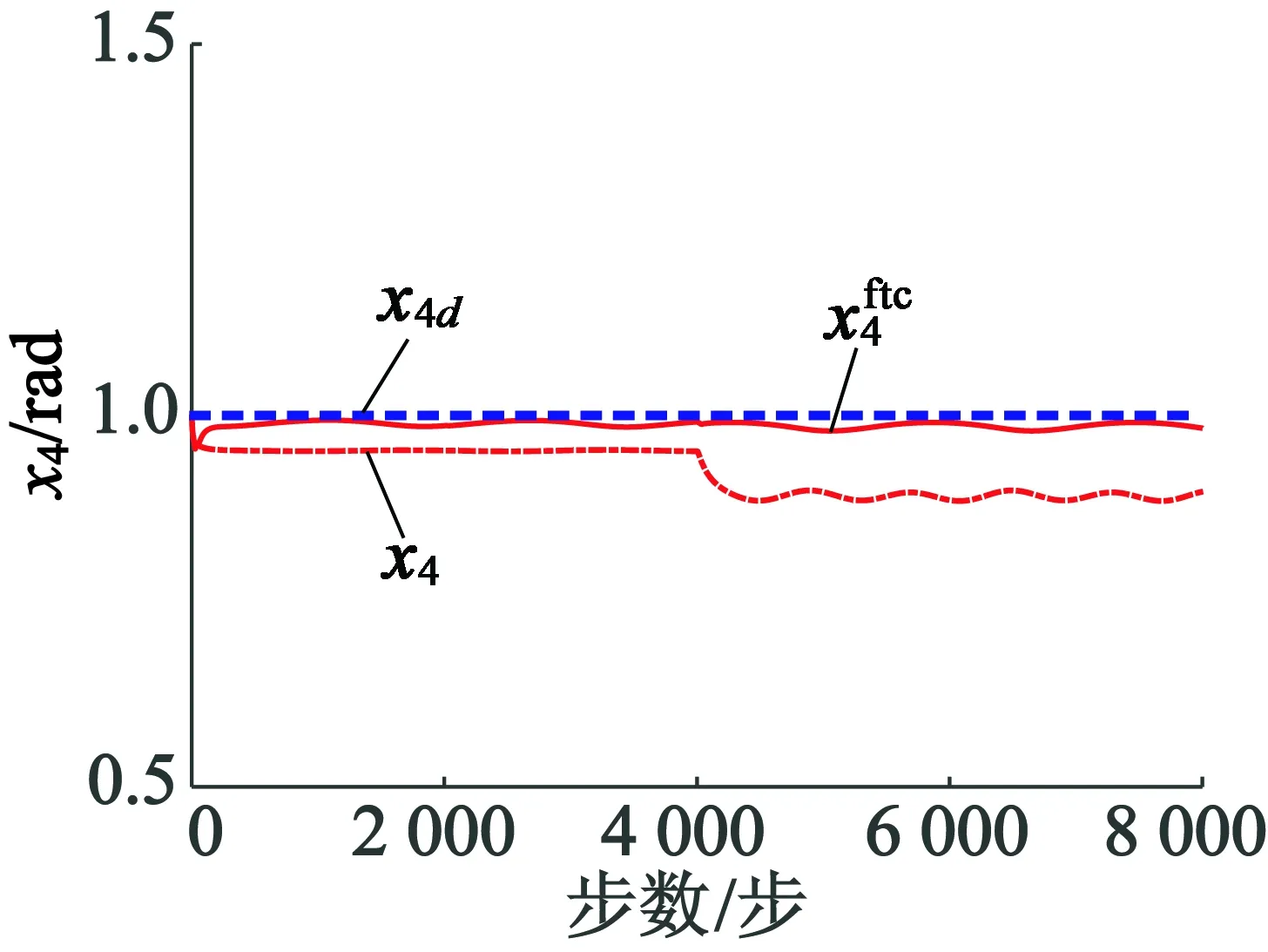
图4 磁链跟踪曲线

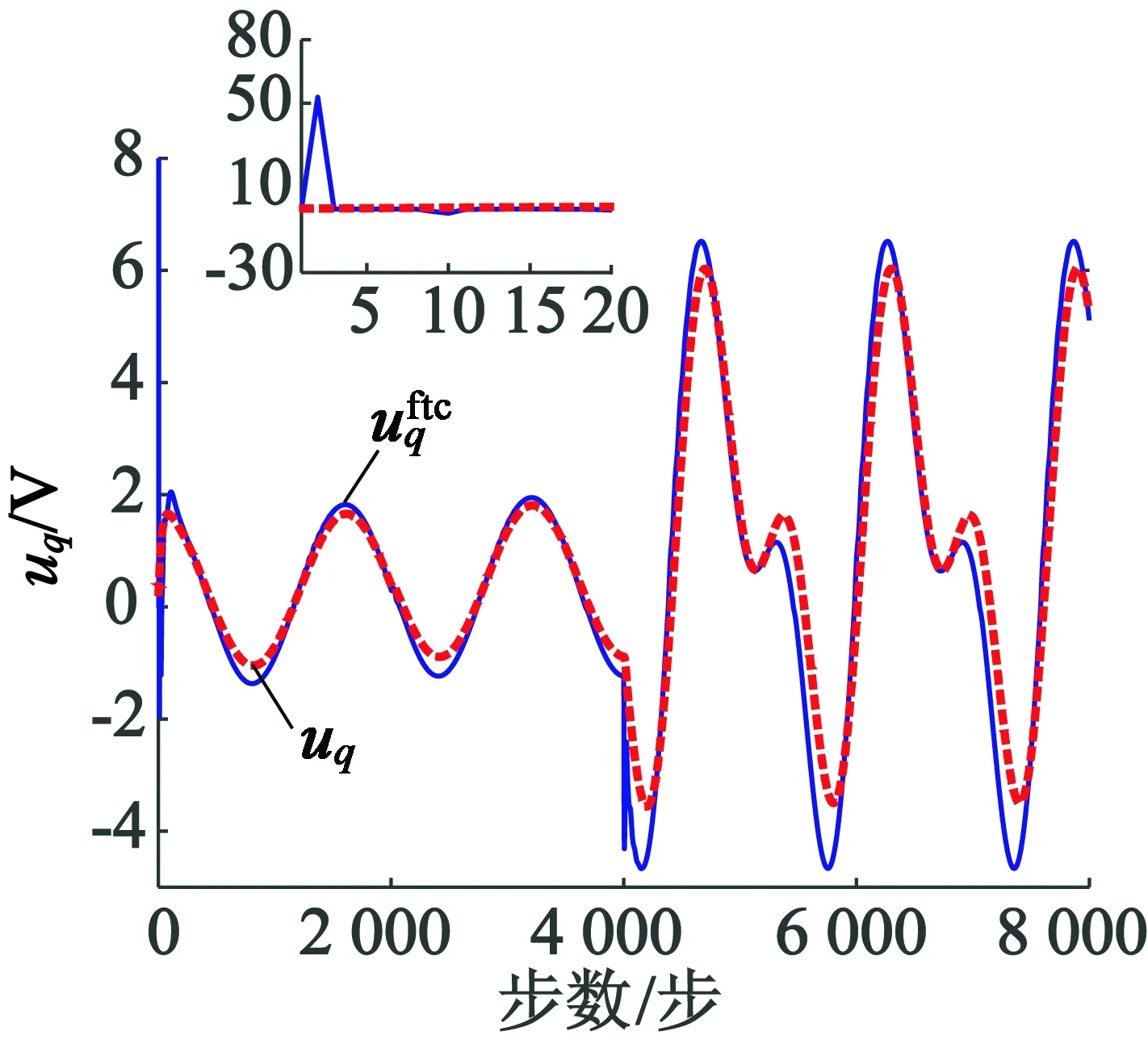
图5 q轴定子电压轨迹曲线

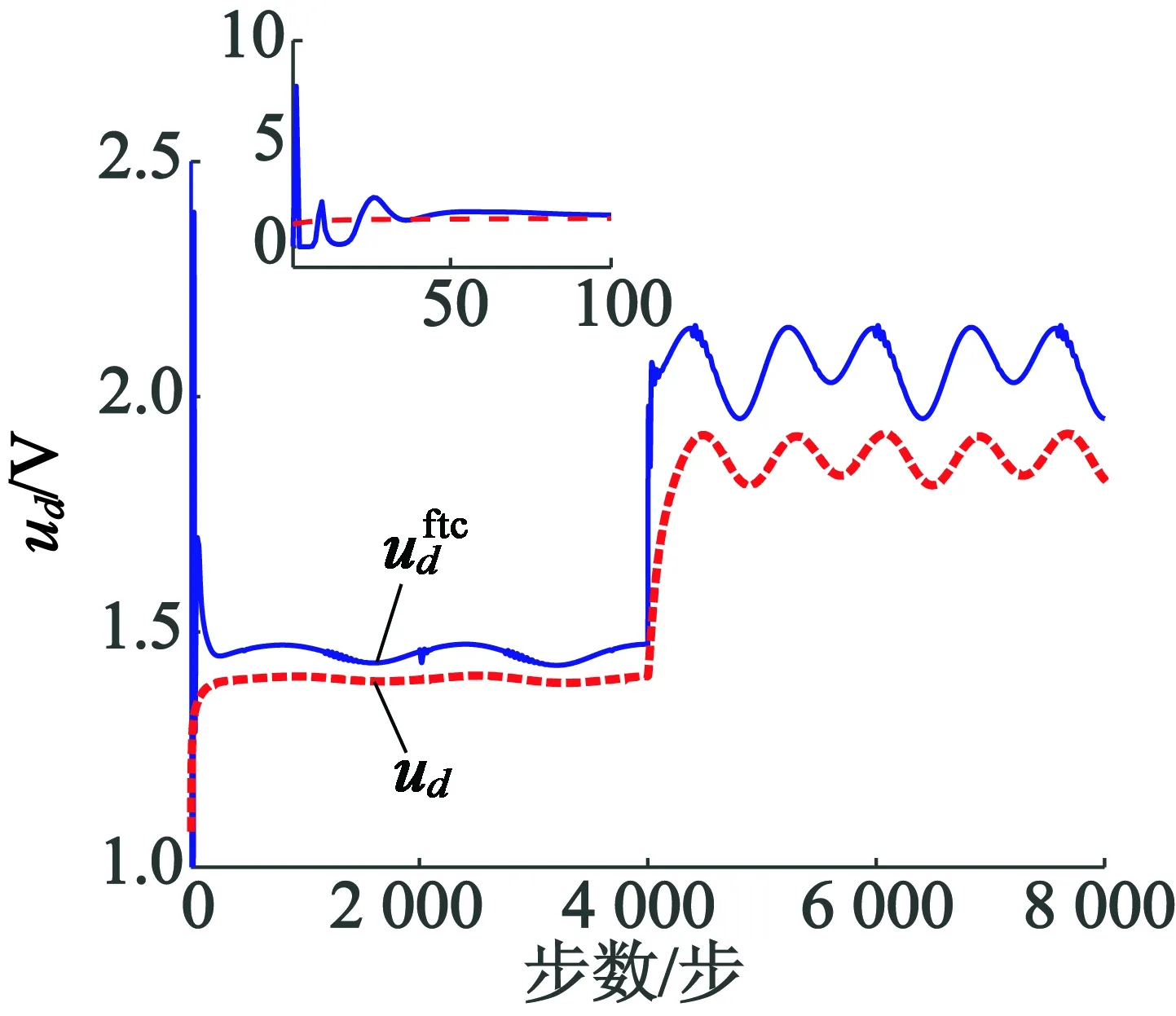
图6 d轴定子电压轨迹曲线

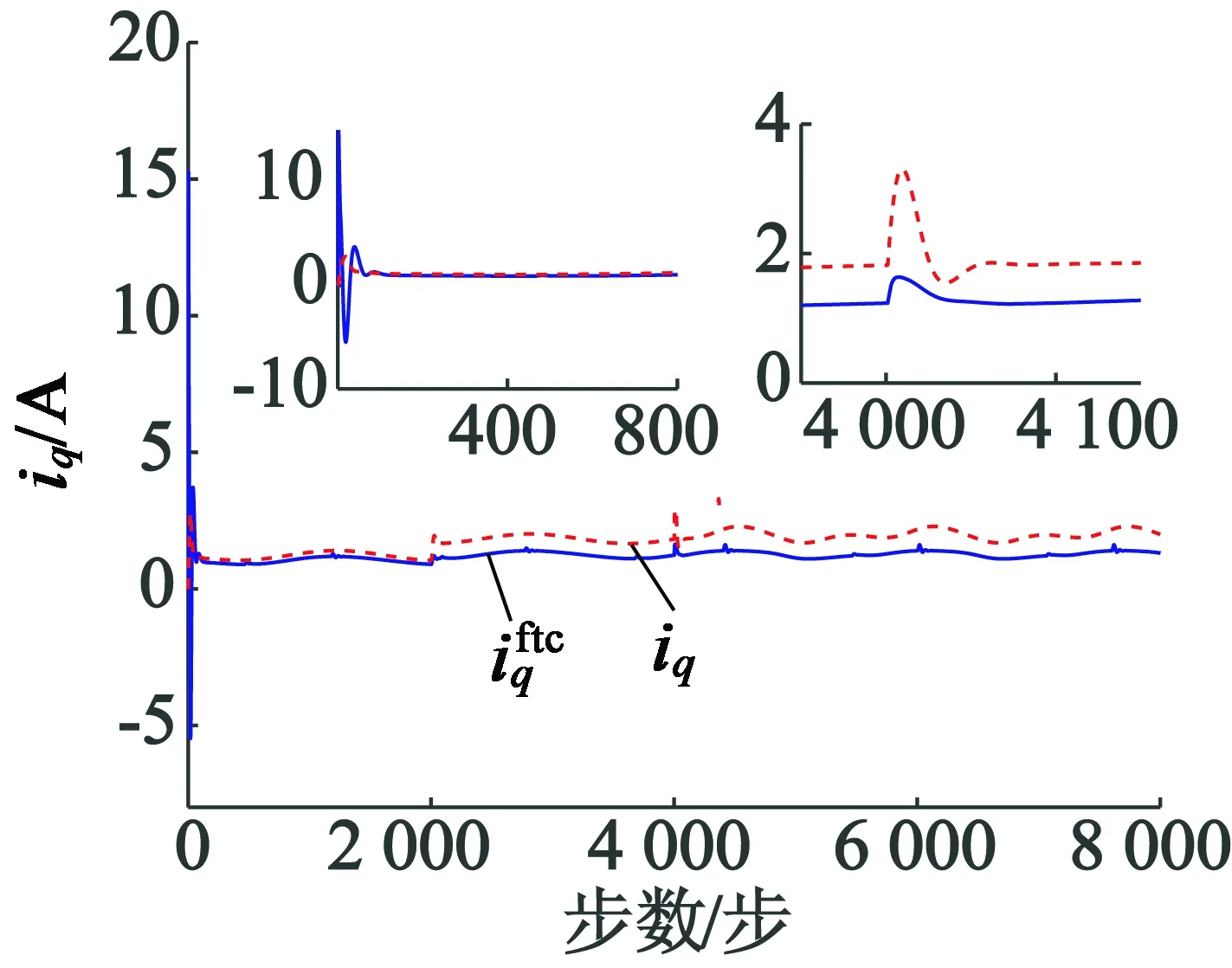
图7 q轴定子电流轨迹曲线

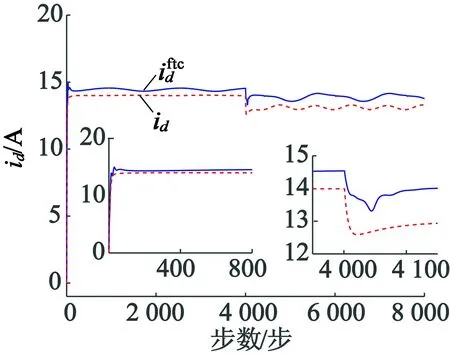
图8 d轴定子电流轨迹曲线

5 结 语

本文研究了基于神经网络的异步电动机离散容错控制方法，设计的控制器同时考虑了执行器失效故障和偏差故障。结合动态面技术和反步法，解决了反步法应用到离散系统中产生的“计算复杂性”和“因果矛盾”问题，并利用自适应神经网络技术实现了异步电动机控制系统的容错控制。最后，通过Lyapunov稳定性分析，证明了闭环系统是半全局一致最终有界的，仿真结果表明本文的容错控制方法在正常和故障状况下均能保证位置跟踪性能，验证了控制方法的有效性。