基于投资视角的讨价还价博弈模型
2020-07-27王一鸣
王一鸣

【摘 要】针对项目治理中利益相关者的利益诉求问题,论文提出了一种基于投资视角的讨价还价博弈模型。首先,论文分析了讨价还价博弈模型及其特点;其次,结合现代项目利益相关者博弈环境特征,建立了罗宾斯坦讨价还价博弈模型;最后,以罗宾斯坦讨价还价博弈模型为基础加入外部变量,建立了一种扩展博弈模型,提高了模型的实用性。
【Abstract】Aiming at the problem of interest demands of stakeholders in project governance, this paper proposes a bargaining game model based on the investment perspective. Firstly, the paper analyzes the bargaining game model and its characteristics; secondly, combining with the characteristics of modern project stakeholders' game environment, the paper establishes the Rubinstein bargaining game model; finally, based on the Rubinstein bargaining game model, the paper adds external variables, establishes an extended game model, and improves the practicability of the model.
【关键词】项目治理;博弈论;投资;利益
【Keywords】project governance; game theory; investment; interest
【中图分类号】F224.32 【文献标志码】A 【文章编号】1673-1069(2020)05-0105-02
1 引言
工程项目作为现代企业参与全球化市场竞争的重要载体,是促进经济增长的主要力量。现阶段,由于项目规模宏大,需要在政府相关部门的宏观调控下协调合作,共同完成项目的建设[1,2]。
为有效提升项目利益相关者之间的合作质量,保证项目的资本收益以及顺利运行。仅仅依赖合同、沟通等手段已无法有效解决项目利益相关者的合作关系,使得对项目中利益相关者的合作博弈关系的研究极为迫切。引用博弈的方式,通过相关流程,能够完成项目利益相关者之间的关系治理。因此,本文提出了一种基于投资视角的讨价还价博弈模型。
2 讨价还价博弈模型及其特点
20世纪80年代,美国著名金融学家马克·罗宾斯坦采用了完全信息下动态博弈的方法,对单一的、无限循环的完全信息下讨价还价的博弈过程进行了模拟研究,并建立了完全信息下的讨价还价博弈模型,也称罗宾斯坦讨价还价博弈模型[3-5]。讨价还价的博弈方式通常被当成合作博弈的一种,同样,其博弈过程也可以当作一种合作博弈过程来进行分析。现代经济社会中,讨价还价被当作谈判中最重要的一项关键内容,因此,熟悉了解讨价还价合作博弈的技巧和方法,并将之熟练地应用在谈判活动中,是促成企业谈判、完成并购价格商议的重要举措。讨价还价博弈模型具有序贯性、反复性、均衡性三个主要特点。
3 项目治理中利益相关者的博弈环境
当今社会,社会分工越来越细化,企业也越来越重视提升各自的核心竞争力,同一个项目由数个企业共同合作完成的现象也渐渐成为主流。当一个企业需要独自完成多个项目建设时,所有项目的资本投入和资本收益均由该企业承担,也就是说,所有的风险均由企业独自承担。企业为了使资本的投入与资本的收益的博弈过程最优,即获得效益最大化,会在参与建设的数个项目中权衡利弊,进行取舍。因此,项目治理中合同角色的形成过程如图1所示。
4 讨价还价博弈模型建立
4.1 讨价还价博弈模型建立
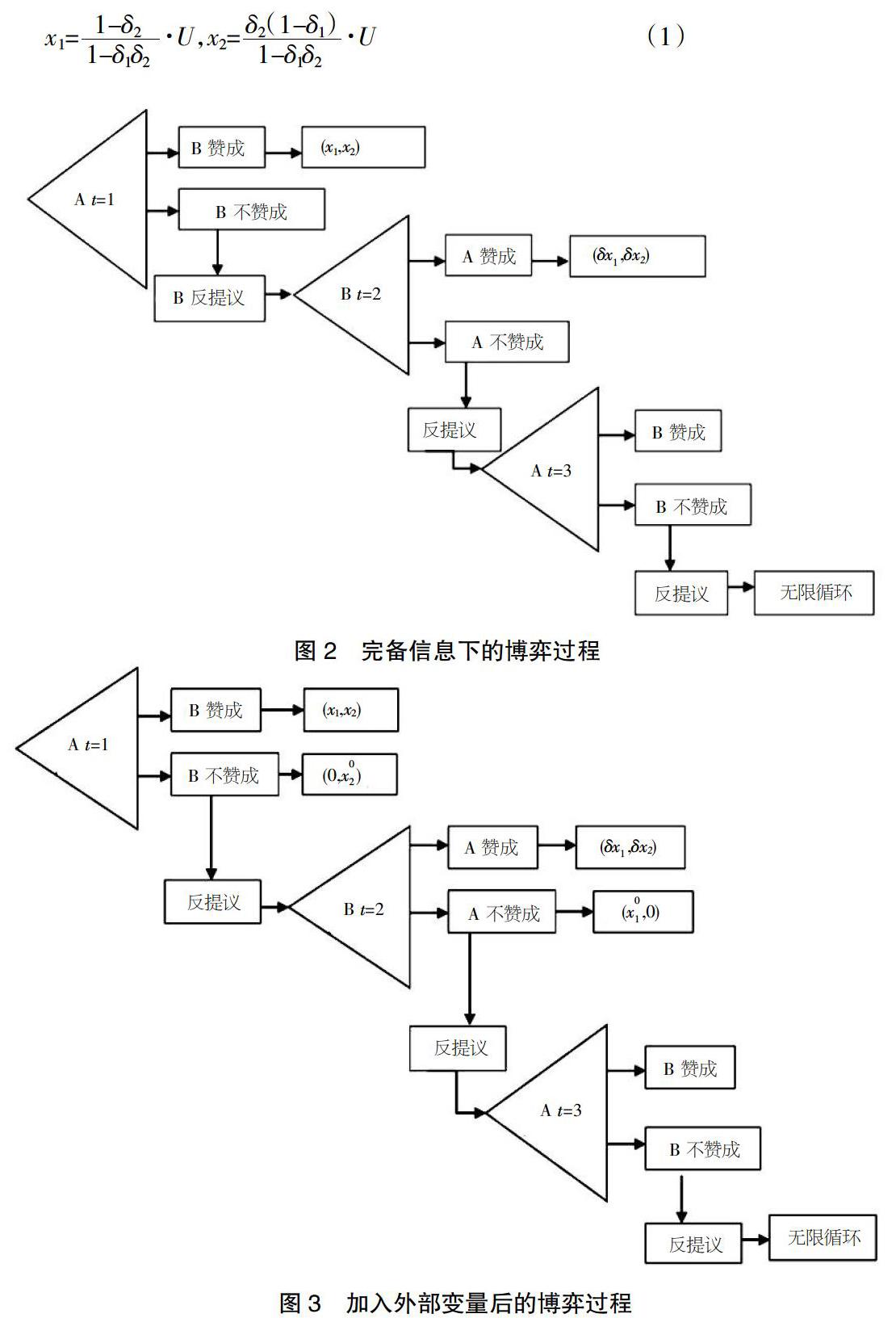
假设在完备信息的情况下,A公司和B公司分配同一单位的利益,A公司和B公司彼此交替出价来进行博弈。首先,A公司提出价格x1,此时B公司所能获得的利益为U-x1。若B公司赞成A公司的提价,则博弈过程结束。如果B公司不赞成A公司的提价,博弈将继续进行。此时B公司进行反提价,A公司进行选择。若A公司同意B公司的提价,则A公司获得的收益为δx1,B公司获得的收益为δx2。假如A公司不赞成B公司的提价,则开始下一轮的博弈。循环往复,直到A公司和B公司达成一致。博弈过程如图2所示。
在完备信息下简单讨价还价的博弈过程中,有唯一的子博弈均衡(SPE,Subgame Perfect Equilibrium)。此时A公司和B公司的收益分别为:
x1=·U,x2=·U (1)
4.2 加入外部变量后的扩展模型建立
上述的博弈过程不存在外部机会收益,而在现实生活中,更多的情况是A公司和B公司同时承担着多个项目的建设。假定各利益相关者为追求利益的最大化放弃项目N。因此,要在上述博弈过程的基础上,加入外部机会收益变量x,x。其中,x是A公司放弃项目N的合作转而投入其他项目后所获得的机会收益,x是B公司放弃项目N的合作轉而投入其他项目后所获得的机会收益。加入外部机会收益变量后的完备信息下的讨价还价博弈模型如图3所示。
将外部机会收益加入无限循环范围内的罗宾斯坦博弈模型后,在博弈的过程中,假设机会对于参与者来说是瞬息即逝的,在t时刻,A公司进行首次提价,若B公司认为没有必要谈判,便可将已投入项目N中的资源转投到其他项目,并得到外部机会收益x。此时A公司因为反应时间的存在,丧失了外部机会收益,所以A公司与B公司的收益分配为(0, x)。同理,若是B公司自第一轮进行提价,A公司选择拒绝时,A公司与B公司此时的收益分配为,x,0)。
5 结语
本文通过对罗宾斯坦讨价还价博弈模型以及其博弈过程进行分析,在不否定项目治理中沟通、信任以及合同等手段对利益相关者的管理效用基础上,建立了一种项目治理中利益相关者合作博弈模型,提高了传统模型的实用性。
【参考文献】
【1】邓斌超,尹贻林,王亦虹,等.大型公共项目总承包模式混合治理研究[J].工程管理学报,2019,33(06):30-35.
【2】代广松,姜骞,田语嫣.关系治理对建筑工程项目质量绩效的影响研究——合作质量的中介效应[J].数学的实践与认识,2019,49(09):70-78.
【3】危恒昌,王军武,程康,等.城市基础设施PPP项目风险分担博弈模型研究[J].建筑经济,2017,38(04):71-75.
【4】左莹.基于讨价还价博弈的企业经理激励研究[D].北京:华北电力大学,2014.
【5】李林,刘志华,章昆昌.参与方地位非对称条件下PPP项目风险分配的博弈模型[J].系统工程理论与实践,2013,33(08):1940-1948.
